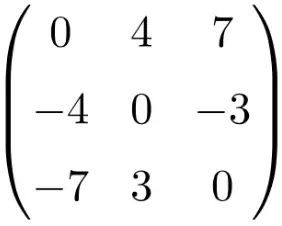在此页面上,我们解释什么是方阵,您将找到方阵的示例。此外,您还将看到方阵具有哪些属性、可以用它们完成的运算以及存在的不同类型。
什么是方阵?
方阵是a 行数与列数相同的矩阵。
方阵的例子
2 阶方阵
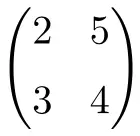
3 阶方阵
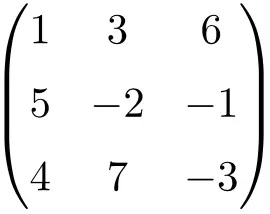
4 阶方阵
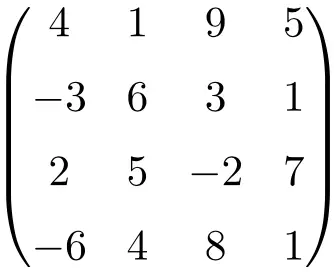
如您所见,方阵通常按阶数命名,即 2 阶方阵意味着它是维度 2×2(2 行 2 列)的矩阵,或者我们称之为 3 阶方阵这表明它的大小为 3×3(3 行 3 列)。
方阵的对角线
方阵的对角线有特定的名称,有主对角线和次对角线:
- 方阵的主对角线由从左上角到右下角的元素组成:

- 方阵的次对角线对应于从左下角到右上角的元素:

方阵的性质
方阵广泛应用于线性代数中,这就是它们如此重要的原因。那么让我们看看是什么特征使此类矩阵如此相关:
- 任何方阵都可以分解为对称矩阵和反对称矩阵之和。
- 如果两个方阵的阶数相同,则它们可以相加或相减:
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2&-3\\[1.1ex] 1&9&7\\[1.1ex] 4&1&-2\end{pmatrix} + \begin{pmatrix}2&3&0\\[1.1ex] 8&6&-4\\[1.1ex] 1&3&-1\end{pmatrix} = \begin{pmatrix}7&5&-3\\[1.1ex] 9&15&3\\[1.1ex] 5&4&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cec5286f22acdb6c84e876264157a89_l3.png)
- 两个方阵可以在两个可能的方向上相乘。但方阵的乘积是不可交换的,即乘法结果会根据乘在哪一边而改变。请注意以下示例中的结果如何取决于矩阵的位置:
![Rendered by QuickLaTeX.com \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix} \cdot \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} = \begin{pmatrix}12&5\\[1.1ex] 20&8\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6bdc76d296851b4ea7aa79124a026a01_l3.png)
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} \cdot \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix}= \begin{pmatrix}23&-5\\[1.1ex] 13&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6405df17f38fb056fe7e5ab9e218f960_l3.png)
- 方阵是唯一可以计算行列式的矩阵。因此,只有当行列式是方阵时才能求解。例如,要找到 3×3 方阵的行列式,您必须应用 Sarrus 规则:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 1 & 3 & 1 \\[1.1ex] 0 & 2 & 4 \\[1.1ex] -1 & 5 & 1 \end{vmatrix} & = \\ & = 1 \cdot 2 \cdot 1 + 3 \cdot 4 \cdot (-1) + 0 \cdot 5 \cdot 1 \ - \\[1.1ex] & \phantom{=} - (-1) \cdot 2 \cdot 1 - 5\cdot 4 \cdot 1 - 0 \cdot 3 \cdot 1 \\[2.5ex] & =2 -12 +0 +2-20-0 \\[2.5ex] & = -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6da09d0b791b047beec0aa2f3da1825_l3.png)
还要记住,如果矩阵的行列式不为0,则说明它是正则矩阵,即是可逆的。另一方面,如果行列式为零,则它是奇异矩阵(没有逆矩阵)。
- 最后,方阵可以对角化。因此可以通过改变基数来计算方阵的特征值(或特征值)和特征向量(或特征向量)。
方阵运算
正如我们所见,只有当矩阵是方阵时才能计算矩阵的行列式。同样,还有一些运算只能在矩阵为平方维时才能执行:
矩阵的迹
矩阵的迹是构成方阵主对角线的元素之和。
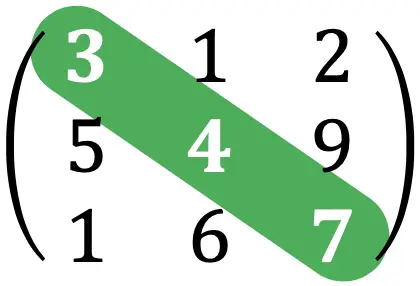
例如,上面练习中矩阵的迹将是:
![]()
方形模具的类型
然后你就有了现有的最重要的方阵类型。单击模具类型以了解其特殊之处。
正如您所看到的,方阵有很多种类型,每种方阵都有自己的名称,原因也各不相同。