数学符号是一种通过使用符号来交流思想和计算的方式。尽管乍一看似乎令人困惑,但经过一些练习,您将能够轻松地理解它。在本文中,我们将向您展示此表示法中使用的所有符号的含义以及如何应用它们的一些示例。
什么是数学符号?
数学符号是数学中使用的一种书写值和表达式的方式。这种技术使数学家能够简洁而精确地陈述想法。数学符号还可以让那些练习或研究数学的人更好地理解概念。
数学语言不应与科学记数法混淆,科学记数法是一种书写数值的方式。同时,数学符号更多的是一组符号,可以让您编写复杂的表达式,就像语言一样。稍后我们将更详细地讨论这个主题。
如何读懂数学符号?
学习解释数学符号比看起来更容易,您只需要学习每个符号的含义,一旦学会,您将能够阅读用数学符号书写的任何内容。就是这么简单,尽管它显然需要练习和大量的学习时间。
数学表达式非常符合逻辑并且总是遵循一定的模式,因此,您只需要记住规则,然后您就会知道如何将它们推断到任何情况。我们甚至可以描述非常复杂的计算,这就是数学语言的魔力,它允许以有条不紊的方式传达非常复杂的消息。
数学符号的组成部分
数学符号由一系列表示数字、运算以及它们之间关系的符号组成。这些符号乍一看可能很复杂,但只要稍加练习和理解,解释数学符号就会变得轻而易举。
接下来,我们将详细解释数学语言中可以找到的四种元素。从最基本的开始,到最复杂和抽象的结束。一旦理论解释完成,我们将讨论存在的数字符号的类型。
数字和数字组
首先,我们必须定义数学数字,它是一个数学概念,表示与单位相关的数量。我们可以按照十进制计数系统并组合以下符号来描述任何数值:0、1、2、3、4、5、6、7、8 和 9。
如果我们根据不同的属性对数字进行排序,我们就会得到几类数字,称为数字集。这些值组也有自己的符号来指定它们,在下面的列表中,我们将它们全部与相应组的名称一起呈现:
这些符号通常用于我们的计算中,以一次性确定各种数字。例如,如果我们有一个相应地接受很多值的表达式,那么我们不用一一写出数字,而是通过它们的数字组对应的符号来指定这些值会更容易。
运算符和量词
现在我们已经讨论了数字,这是数学的本质,我们需要谈谈运算符和量词。第一个是允许我们表示运算的所有符号:加法 (+)、减法 (-)、乘法(x 或·)、除法 (÷) 等。
然而,我们还有另外两种类型的运算符,它们是逻辑运算符和关系运算符。第一个表达合取、析取和否定。它们帮助我们提出逻辑运算,与算术运算不同,逻辑运算不适用于数字,而是适用于数学命题。
而第二个允许我们在值或数学表达式之间建立等价和关系。这些符号可用于算术计算(对数字进行排序),但当我们有变量时,它们在代数中更重要(在两节中详细介绍)。
在下面的列表中,您可以找到我们迄今为止讨论过的所有运算符的定义:
| 象征 | 定义 | 种类 |
| + | 添加 | 算术运算符 |
| – | 减法 | 算术运算符 |
| X, *, · | 乘法 | 算术运算符 |
| ÷ | 分配 | 算术运算符 |
| x² | 赋权 | 算术运算符 |
| √ | 订金 | 算术运算符 |
| 和 | 连词 | 逻辑运算符 |
| 任何一个 | 析取 | 逻辑运算符 |
| 不 | 否认 | 逻辑运算符 |
| = | 等于 | 关系运算符 |
| > | 大于 | 关系运算符 |
| < | 小于 | 关系运算符 |
| >= | 优于或等于 | 关系运算符 |
| <= | 小于或等于 | 关系运算符 |
| ≠ | 不等于 | 关系运算符 |
| == | 一模一样 | 关系运算符 |
| ≈ | 几乎相等 | 关系运算符 |
| ≃ | 相当于 | 关系运算符 |
| ∝ | 成比例的 | 关系运算符 |
虽然还有其他五个逻辑运算符,它们用于从集合论解释数理逻辑。这是应用集合逻辑的分支,用于计算、几何、统计……然后,我们向您展示所使用的符号及其定义。
| 象征 | 定义 |
| x ∈ A | x 属于 A |
| x ∉ A | x 不属于 A |
| ∪ | 联盟 |
| ∩ | 路口 |
| ⊂ | 包容性 |
至于量词,我们可以将它们定义为表示集合中满足一定条件(等价、顺序、隶属等)的元素数量的符号。运算符有很多种,但我们可以重点介绍最常用的运算符:
| 象征 | 定义 | 种类 |
| ∀x | 对于所有x | 量化 |
| ∃x | 至少有一个x | 量化 |
| ∄x | 没有x | 量化 |
| ∃!x | 只有一个x | 量化 |
| | | 例如 | 量化 |
| ∴ | 所以 | 量化 |
数学表达式及其关系
通过到目前为止我们介绍的符号,您可以理解很多数学知识,但我们尚未解释它们在复杂表达式中的应用或关系,例如组合运算或代数计算。另外,还有一些关系符号需要讨论。这些是我们将在本节中看到的。
从分组符号开始,它们是括号、方括号和花括号。这些元素对于复杂公式的指定至关重要。它的主要功能是在全局表达式中优先考虑某些计算。并且这三种类型之间有不同的优先级。在这个表达式中,您可以看到书写顺序 3 {[2 + (3 – 2) · 2] – 4}。
| 符号 | 定义 | 优先事项 |
| “(“和”)” | 插入语 | 最高优先级 |
| “[“和”]” | 括号 | 第二优先 |
| “{“ 和 ”}” | 按键 | 第三优先 |
为了完成这个类别,我们将讨论求和 (Σ)和乘积 (∏) ,这些元素使我们能够描述重复的加法和乘法。求和相当于说:“Xi 的和,其中 i 取从 1 到 an 的值”。产品是相同的,但我们不是加,而是乘。
代数分析
关于代数符号,首先要讨论的是变量,它由字母表中的字母表示。它们的功能是模仿数字,但它们不像数学常量那样具有固定值,因此它们可以采用新值。这适用于方程、极限、导数、积分、矩阵……
最后,我们想谈谈我们刚刚在最后一段中讨论的所有这些代数运算的表示。从那时起,它们就是代数的基础,你需要知道它们的符号系统是什么。接下来,我们向您展示一个带有不同符号和简要定义的表格:
| 象征 | 定义 |
| 林x → b | 极限(当x趋于b时) |
| y’, f’ (x), dy / dx | 衍生物 |
| ∫ | 完全的 |
| 至MXN | mxn 维度的矩阵 |
数学语言符号的结论
到目前为止,您已经看到了数学中涵盖的所有重要符号,显然还有更多要讨论的内容。但是,这些对于数学的每个子类别来说更为具体:几何、统计、代数……因此,我们将结束这个主题并讨论数字符号。
数字符号的类型
在本节中,我们将看到表达数学数字的所有方法,因为有不同的表示法。一开始,我们在上面提到了十进制,这是数学家使用最多的。接下来,我们将更详细地解释它并向您展示其他类型的数学符号:
小数记数法
十进制数字系统是一种位置数字系统(其中每个数字的位置将决定其值的系统)基于数字 10 的倍数和约数。因为十是用作数字基数的数字。因此,我们将使用的十个数字符号是:1、2、3、4、5、6、7、8、9和0。
这些数字的值由数字之和乘以基于 10 的幂确定,根据位置建立。记住这一点非常重要:要写出小于一的数字,必须使用小数点。下面是一个例子:
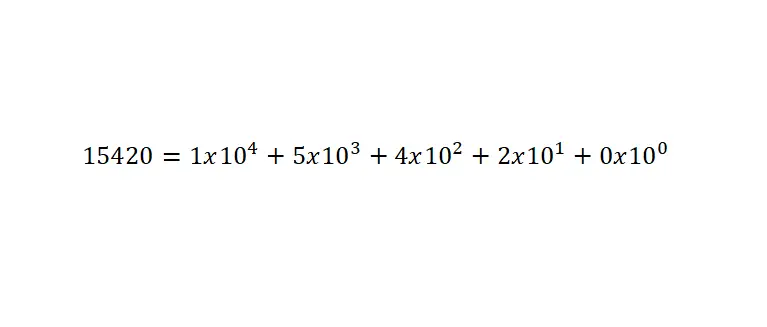
科学计数法
指数形式表示法或科学表示法显然是科学技术中最常用的书写类型之一。事实上,这使我们能够以简单的方式表达非常大和非常小的数字。为了理解科学记数法的定义,我们将解释如何将整数传递给该记数法:
- 移动小数点:您必须根据需要多次移动小数点,直到到达第一个数字(如果数字很大,则移动到左边;如果数字很小,则移动到右边)。
- 建立底数:写下最后一个数字乘以十,因此,在将小数点移到一侧得到的值旁边,必须写下乘以十:“x 10”。
- 添加指数:其值等于小数点移动的次数。对于较大的数字,您将把指数保留为正数,但是对于较小的数字,您必须将其写为负号。
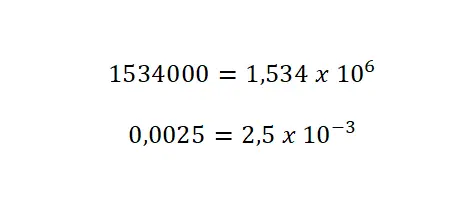
十六进制表示法
十六进制系统基于 16,这意味着它使用 16 个不同的符号:0、1、2、3、4、5、6、7、8、9、A、B、C、D、E 和 F看,这个编号系统是由十进制数字和六个字母组成的。这种表示法通常用于 IT 以及与 IT 相关的一切领域。
需要澄清的是,由于它具有与其他类型的表示法相同的符号,因此我们必须始终通过括号和索引 16来表明它是十六进制书写的。在下面的示例中,您可以从一个非常清晰的示例中看到十六进制数到十进制表示法的转换:
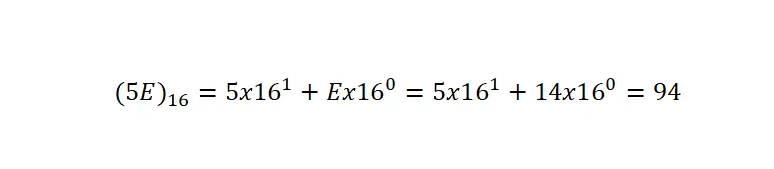
要将十六进制数转换为十进制表达式,我们需要将数字分解为其基数乘法,就像我们在十进制表示法中所做的那样,但将基数更改为 16 。接下来,我们将每个数字乘以 16,直到该特定数字占据的位置减一。
八进制表示法
我们要讨论的最后一个系统是八进制表示法,它的基数为 8。这意味着它只使用八个符号或数字:0、1、2、3、4、5、6 和 7。是最少使用的我们已经解释过的所有编号系统。应当注意的是,该符号的转换是根据与先前的相同的过程来进行的。
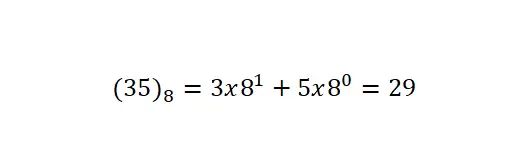
新颖的符号
最后我们可以谈谈罗马数字系统,它在今天还没有被广泛使用,但在过去它在数学领域非常重要。因为它是将数学带入生活的符号之一。
您的写作仅限于 7 个符号:I (1)、V (5)、X (10)、L (50)、C (100)、D (500) 和 M (1000)。通过组合这些字母,所有的数字就被写出来了。如果您想知道它们如何结合起来产生其他更大的数字,我们建议您阅读我们关于它们的文章,通过最后一个链接进行访问。
如何提高数学符号的阅读能力?
有多种方法可以提高阅读数学符号的能力。一种方法是大声读出符号和数字。另一种方法是熟悉符号及其含义。您还可以使用练习和问题来练习阅读数学符号。
我们希望本指南对您有所帮助,如果您有任何疑问,请随时在评论中写下。或者,如果您想对该主题做出贡献,我们也希望在评论中看到。也就是说,我们给您留下了一篇关于如何学习数学的文章,以防您想继续阅读。