在此页面上,我们解释如何对数字进行多项式分解(或表达式)。在这里您可以看到多项式分解的示例,此外,您还可以找到已解决的分步练习来练习。
什么是数的多项式分解?
在数学中,数字的多项式分解包括用总和来表示该数字,这样总和的每一项都是该数字的每个数字与以 10 为底的幂的乘积。
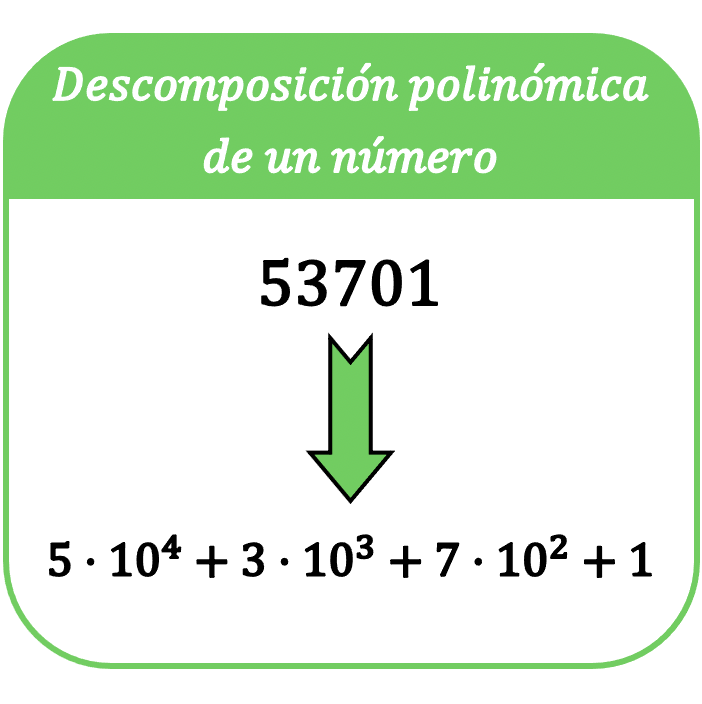
术语“数的多项式分解”也称为“数的多项式表达式” 。
如何进行多项式分解
要对数字进行多项式分解,必须将数字的每一位数字乘以 10 的右边位数。
例如,如果我们要计算以下数字的多项式分解:
![]()
在本例中,数字 8 占据第五位,因此它的右侧有 4 位数字。因此,我们必须将八乘以十的四次方:
![]()
因此,要对数字 86293 进行多项式分解,您必须对该数字的所有数字执行相同的操作,并以和的形式表示所有乘法:
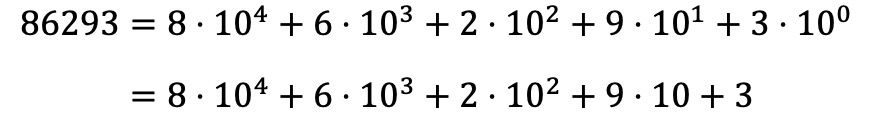
请注意,10 0次幂消失了,因为根据幂的性质,任何数升到0 都等于1,因此10 0 =1。
另一方面,您还可以从乘法分解中找到数字的多项式分解:
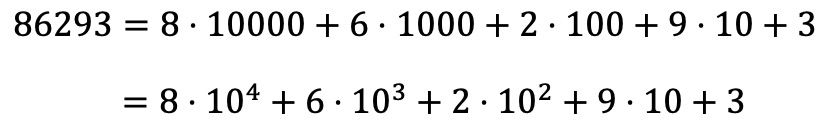
数字多项式分解的示例
一旦我们了解了如何进行数字的多项式分解,我们将看到此类运算的不同示例,以充分理解该概念。
- 3641 的多项式分解:
![]()
- 56912 的多项式分解:
![]()
- 27084 的多项式分解:
![Rendered by QuickLaTeX.com \begin{aligned} 27084 &= 2\cdot 10^4 +7\cdot 10^3 +0\cdot 10^2 + 8\cdot 10 + 4 \\[2ex] & = 2\cdot 10^4 +7\cdot 10^3 + 8\cdot 10 + 4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f72230330ff9c9150dc9ab19a89a42d8_l3.png)
在最后一个例子中,我们可以简化第三次乘法,因为任何数字乘以零都会抵消。
十进制数的多项式分解
我们刚刚看到了如何执行自然数的多项式分解。但是……如何分解十进制数多项式?
那么,十进制数的多项式分解的方式与整数相同,但此外,我们将每个十进制数乘以以 10 为底的幂的乘积相加,该幂的指数是该数字所占据的小数位置,并且带有负数符号。
用文字解释这似乎非常复杂,但是您会发现通过示例可以更好地理解:
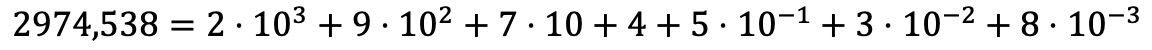
解决多项式分解练习
为了让您可以练习进行多项式分解,我们准备了几个逐步解决的练习。
不要忘记您可以在评论中向我们询问任何问题! 🤔🤔🤔
练习1
对以下数字进行多项式分解:
![]()
![]()
![]()
![]()
要求任意数字的多项式分解,请将该数字的每个数字乘以 10 乘以右侧的位数,然后将所有乘积相加。然而:
![]()
![]()
![]()
![]()
练习2
求下列数字的多项式分解:
![]()
![]()
![]()
![]()
要对一个数进行多项式分解,必须将该数的每一位乘以 10 乘以它右边的位数,然后将所有乘积相加。然而:
![]()
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned} 3030 & = 3 \cdot 10^3+ 0\cdot 10^2 +3 \cdot 10 +0 \\[2ex] &= 3 \cdot 10^3+3 \cdot 10 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e3500d6a94685566b267e8708e8b0d7_l3.png)
![]()
![]()
练习3
计算以下十进制数的多项式分解:
![]()
![]()
![]()
![]()
在这个问题中,所有数字都是十进制的,因此要分解它们,您必须将每个非十进制数字乘以 10(提高到小数点后的位数),并将每个十进制数字乘以 10(提高到其小数点位置)一个负号。
![]()
![]()
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned} 0,82694 & = 0 + 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\\[2ex] & = 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-deb6b85265df2e98bcb5e116e19c397f_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned} 5,7201 & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+0\cdot 10^{-3}+1\cdot 10^{-4}\\[2ex] & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+1\cdot 10^{-4} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e204c24ba4f9138f503cf2c2a0e379d_l3.png)