在本页中,我们解释如何获取(或提取)多项式的公因式。在这里您将找到不同类型的公因数,并且您将能够看到如何实现这一点的几个示例。此外,您还可以通过逐步解决的练习进行训练。
公因数是什么?
在数学中,公因数是多项式所有项中都存在的因数,即公因数由与多项式每一项相乘的数字或字母组成。
作为一个例子,我们将确定以下多项式的公因数是什么:
![]()
在第 4 项,多项式的所有项都重复:
![]()
因此,该多项式的公因数等于 4。
![]()
如何获得(或提取)公因数
了解了公因数的含义后,让我们看看如何从多项式中获取公因数。
当多项式的两项或多项具有公因数时,可以取(或提取)该公因数来将多项式的加法或减法变换为乘法。
这看起来可能有点难写,所以让我们通过一个例子来看看如何从多项式中提取公因数:
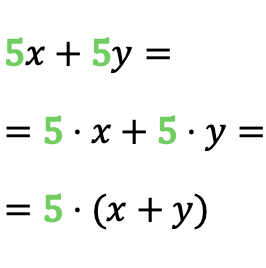
正如您在示例中看到的,数字 5 在单项式 5x 和单项式 5y 中重复出现,因此多项式的公因数为 5。因此,一旦确定了公因数,我们就可以将单项式之和转换为产品。
提取公因数时不要忘记加上括号,因为公因数必须乘以所有加数。
去掉公因数就是分配律的逆运算,即我们实际上是在逆向应用分配律。因此,我们总是可以通过执行相反的过程来验证我们是否正确提取了公因子:
- 如果通过应用分配律我们从一开始就得到了相同的多项式,这意味着我们已经正确地得到了公因子。
- 另一方面,当使用分配性的结果是另一个与原始多项式不同的多项式时,则意味着我们在提取公因子的过程中犯了错误。
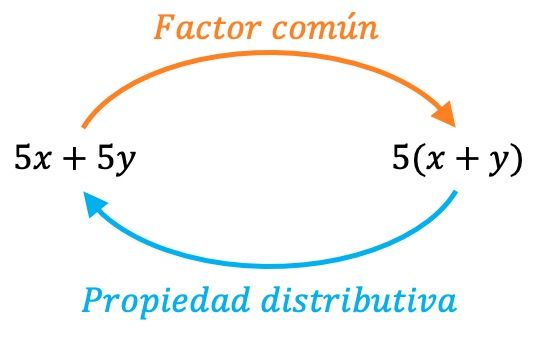
公因数取(或提取)的示例
我们给您提供更多示例来完成对公因数概念的理解:
实施例1
正如您在此示例中看到的,可以同时从两个以上的项中提取公因子:
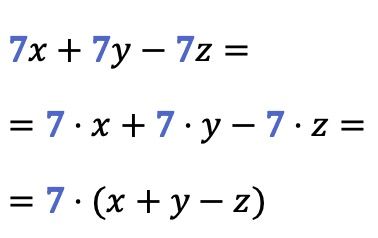
实施例2
您还可以从变量(或字母)中提取公因子:
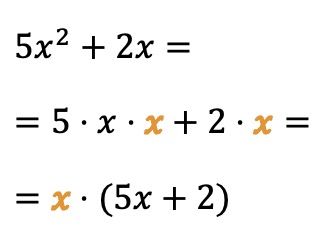
在这种情况下,字母 x 乘以多项式的两项,因此我们可以通过将变量 x 作为公因子来简化代数表达式。
实施例3
在此示例中,第一项的变量 x 为 3 次方,第二项中的 x 为 2 次方,因此两项都有两个 x。因此,公因子不仅仅是 x,而是 x 2 :
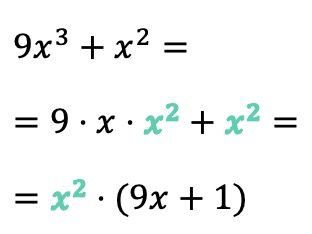
另一方面,请注意,如果多项式的公因式与一项完全一致,那么当我们提取公因式时,我们必须在其位置上放一个 1 。否则,如果我们没有在其位置上放置任何东西,我们就不会得到等效的表达式。

实施例4
有时公因数并不那么明显,也不是直接可见的,而是单项式系数的除数。例如,以下示例中的公因数为 3,因为 6 和 9 的阶乘分解包含 3:
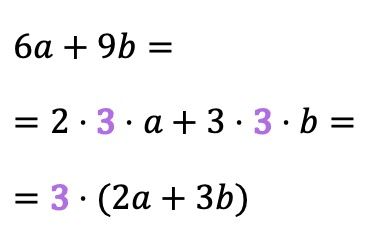
这种类型的公因数在一些代数书籍中被称为最大公因数,因为该公因数同时是多项式项的系数的最大公因数(GCD)。
如果您已经做到了这一步,这意味着您可能已经知道如何找到多项式的公因子,完美。但是,您是否想知道公因数的用途是什么?公因式的一种应用是用于对多项式进行因式分解。如果您仍然不知道它是什么,在此链接中您可以了解什么是多项式因式分解以及为什么公因式对于执行此多项式运算如此重要。
分数的公因数
公因数对于将项简化为分子和分母为多项式的分数也非常有用。
为了了解这是如何完成的,让我们以简化以下分数为例:
![]()
我们需要做的第一件事是找到分子多项式和分母多项式的公因数。在这种情况下,两个多项式的公因子是 2:
![]()
现在让我们提取两个多项式的公因子:
![]()
一旦我们获得了两个多项式的公因子,我们就需要删除分子和分母中重复的因子:
![]()
总之,简化分数为:
![]()
按分组的公因数
减少多项式项的一种方法是通过对项进行分组来使用公因子法,也称为双公因子提取。顾名思义,该过程包括通过将多项式的项分组两次来简化多项式的表达式。
这个方法有点复杂,所以让我们看看如何使用以下多项式逐步应用它:
![]()
我们首先需要确定两个不同的可能的公因数,因此我们将多项式分为两部分:
![]()
在这种情况下,元素 x 2和 2x 将字母 x 作为公因数,项 5x 和 10 将 5 作为公因数(因为 10 是 5 的倍数)。所以我们有两个共同点:
![]()
![]()
最后,由于其余两个多项式乘积的因子为 (x+2),因此我们可以将多项式简化如下:
![]()
正如你所看到的,这个方法一点也不简单。因此,如果您有任何问题,请随时在评论中向我们提问,我们会尽快答复。
公因数练习一步一步解决
我们让您练习几个逐步解决的问题,以便您可以练习从多项式中提取公因数。
练习1
从以下多项式中提取公因数:
![]()
![]()
![]()
![]()
A)组成第一个多项式的所有项均为 6,因此该多项式的公因数为 6:
![]()
B)在第二个多项式中,其所有元素都至少有一个字母 x。这是多项式的公因数:
![]()
C)多项式的第一个单项式显然是2,第二个单项式是2的倍数。所以多项式的公因数是2:
![]()
D)在最后一个多项式中,所有变量都至少平方。因此,公因数为 x 2 :
![]()
请记住,当公因数与某个项相同时,必须在其位置上添加 1。
练习2
考虑以下多项式的公因数:
![]()
![]()
![]()
![]()
A)构成第一个多项式的所有元素的系数都是 2 的倍数,因此,通过提取公因子,多项式变为:
![Rendered by QuickLaTeX.com \begin{array}{l} 8x^2 + 10y^3 = \\[2ex] = 2\cdot 4x^2 +2\cdot 5y^3 = \\[2ex] = \bm{2\left(4x^2+5y^3\right)} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7862ee57cf098358e43d3b669e0cb54d_l3.png)
B)多项式的所有项中至少有一个 x,因此:
![Rendered by QuickLaTeX.com \begin{array}{l}5x^3-2x^2+4x = \\[2ex] = 5x^2\cdot x-2x\cdot x+4\cdot x= \\[2ex] =\bm{x\left(5x^2-2x+4\right)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-39551a1ffc0b98f8b9c037fdcc793b01_l3.png)
C)多项式所有项的系数的最大公约数为5,因此该多项式的公约数为5:
![Rendered by QuickLaTeX.com \begin{array}{l}25x^5+15x^3-20 = \\[2ex] =5\cdot 5x^5+5\cdot 3x^3-5\cdot 4 = \\[2ex] = \bm{5\left(5x^5+3x^3-4\right)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fe8cc019c3511734ff278f68c44066df_l3.png)
D)多项式中的所有项至少有一个 x,而且所有系数都是 3 的倍数。因此,多项式的公因子是 3x:
![Rendered by QuickLaTeX.com \begin{array}{l}9x^4-3x^3-21x^2-6x = \\[2ex] = 3x^3\cdot 3x-x^2\cdot 3x-7x\cdot 3x-2\cdot 3x= \\[2ex] = \bm{3x\left(3x^3-x^2-7x-2 \right)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fb70701f39b1050eec730f1591671293_l3.png)
练习3
找到以下每个多项式的公因式并减去它:
![]()
![]()
![]()
![]()
A)所有单项式至少有字母
![]()
平方和字母
![]()
立方,所以公因数是
![]()
![Rendered by QuickLaTeX.com \begin{array}{l} 4a^2b^5+7a^4b^3-10a^6b^4 = \\[2ex] = 4b^2\cdot a^2b^3+7a^2\cdot a^2b^3-10a^4b\cdot a^2b^3 = \\[2ex] = \bm{a^2b^3\left(4b^2+7a^2-10a^4b\right)} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b622844f35f4bd4411c545c352331943_l3.png)
B)多项式的所有系数都是 8 的倍数,而且它们至少有 x 2和 y 2作为文字部分。因此,多项式的公因数为 8x 2 y 2 。
![Rendered by QuickLaTeX.com \begin{array}{l}16x^4y^7z+8x^2y^2z^2+ 24x^3y^5 = \\[2ex] = 2x^2y^5z \cdot 8x^2y^2 +z^2\cdot 8x^2y^2+ 3xy^3\cdot 8x^2y^2= \\[2ex] =\bm{8x^2y^2\left(2x^2y^5z+z^2+3xy^3\right)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2d7018f427d800f6db67335a4d4f238b_l3.png)
C)在这种情况下,公因子与中间单项式的值一致
![]()
,因为其他单项式的系数是
![]()
绝对每个人都有
![]()
![Rendered by QuickLaTeX.com \begin{array}{l}6ab^2c^4-6ab^2c+12a^3b^2c = \\[2ex] =c^3\cdot 6ab^2c -1\cdot 6ab^2c+2a^2 \cdot 6ab^2c = \\[2ex] = \bm{6ab^2c\left(c^3-1+2a^2\right)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-76f91563726822a51c7bfe88aa461e6d_l3.png)
D)在这种特殊情况下,多项式没有公因子,因为多项式的所有项中没有重复的因子。因此,多项式不能进行代数简化。
![]()
练习4
通过取公因子来简化以下代数分数:
![]()
![]()
![]()
![]()
化简代数分数(即具有多项式的分数)的过程是从分数的分子和分母中提取公因子,然后消除上面和下面重复的因子。低于分数。所以:
![Rendered by QuickLaTeX.com \text{A)} \quad \begin{array}{l} \cfrac{10x^2+30}{5x-20}= \cfrac{5\cdot 2x^2 +5\cdot 6}{5\cdot x-5\cdot 4} = \\[4ex] = \cfrac{5(2x^2+6)}{5(x-4)}= \cfrac{\cancel{5}(2x^2+6)}{\cancel{5}(x-4)} = \\[4ex] = \cfrac{\bm{2x^2+6}}{\bm{x-4}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ce28a7207aa3bccea5a8afae54c8ad5_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \quad \begin{array}{l} \cfrac{16x^2-8}{24x-32} = \cfrac{8 \cdot 2x^2+8 \cdot (-1)}{8 \cdot 3x-8 \cdot 4} =\\[4ex] = \cfrac{8(2x^2-1)}{8(3x-4)}= \cfrac{\cancel{8}(2x^2-1)}{\cancel{8}(3x-4)} =\\[4ex] = \cfrac{\bm{2x^2-1}}{\bm{3x-4}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a6024cf2af6c13d0d27f7e5d3e675362_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \quad \begin{array}{l}\cfrac{49x^3+7x}{35x^2-14}=\cfrac{7x\cdot 7x^2+7x\cdot 1}{7 \cdot 5x^2+7\cdot (-2)} =\\[4ex] = \cfrac{7x(7x^2+1)}{7(5x^2-2)}= \cfrac{\cancel{7}x(7x^2+1)}{\cancel{7}(5x^2-2)}=\\[4ex] = \cfrac{\bm{x(7x^2+1)}}{\bm{5x^2-2}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5678b7c6d631a693a86fad40aa79d030_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \quad \begin{array}{l} \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}=\cfrac{4x^2\cdot 2x^2+4x^2\cdot 4x+4x^2\cdot (-1)}{4x\cdot 3x+4x\cdot 5}=\\[4ex] = \cfrac{4x^2(2x^2+4x-1)}{4x(3x+5)}= \cfrac{\cancel{4}x^{\cancel{2}}(2x^2+4x-1)}{\cancel{4}\cancel{x}(3x+5)}=\\[4ex] = \cfrac{\bm{x(2x^2+4x-1)}}{\bm{3x+5}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-82199184b3594c18db6888c58fa0bdfc_l3.png)
练习5
取下列多项式的公因数:
![]()
![]()
![]()
![]()
A)多项式的所有项都可以分解为三次阶乘,因此:
![Rendered by QuickLaTeX.com \begin{array}{l} \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}= \\[3ex] = \cfrac{1}{3}\cdot 7x^2+ \cfrac{1}{3}\cdot 8x-\cfrac{1}{3}\cdot 2 = \\[3ex] = \mathbf{\cfrac{1}{3}}\bm{\left(7x^2+8x-2\right)} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-66174ecc5c7264ae95507f632d1f2630_l3.png)
B)根内多项式的公因数为 4,那么我们可以通过计算其平方根来输出公因数:
![Rendered by QuickLaTeX.com \begin{array}{l}\sqrt{12x^3+16}= \\[2ex] =\sqrt{4\cdot 3x^3+4\cdot 4}= \\[2ex]=\sqrt{4\left(3x^3+4\right)}= \\[2ex] =\bm{2\sqrt{3x^3+4}}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3a362644fe5b22fefc962f164db26f5e_l3.png)
C)在这个多项式中,我们可以应用通过分组来提取公因子的过程:
![Rendered by QuickLaTeX.com \begin{array}{l}x^2+4x-3x-12= \\[2ex] =x(x+4)-3(x+4) = \\[2ex] = \bm{(x+4)(x-3)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd43d5f40797c39b0401769ff392d9e5_l3.png)
D)多项式的所有分数系数都是一半的倍数,因此多项式的公因数是 1/2。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle \frac{3}{4}x^2+ \frac{1}{2}x-\frac{5}{6}= \\[4ex] \displaystyle = \frac{1}{2}\cdot\frac{3}{2}x^2+ \frac{1}{2}\cdot x-\frac{1}{2}\cdot\frac{5}{3}= \\[4ex] \displaystyle = \mathbf{\frac{1}{2}}\bm{\left(}\mathbf{\frac{3}{2}}\bm{x^2+x-}\mathbf{\frac{5}{3}} \bm{\right)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a35ab3db2e1f1197d6652e6d4d0a8a8a_l3.png)
👇👇👇 看完这个解释你觉得怎么样?你喜欢它吗?另请记住,如果您对如何确定多项式的公因式有任何疑问,或者您不理解某个练习,您可以随时在评论中询问我们,我们会回答您。 👇👇👇