指数函数

17 9 月, 2023

在此页面上，您将了解什么是指数函数以及如何在图形上表示指数函数。此外，您将看到它的所有特性和几个示例以充分理解它。最后，您将能够通过指数函数的练习和逐步解决的问题进行练习。

什么是指数函数？

指数函数的定义如下：

在数学中，指数函数是自变量x为幂指数的函数。换句话说，它们如下：

$f(x)=a^x$

金子

$a$

是一个不同于 1 的正实数。

指数函数的示例

以下函数是指数函数的示例：

$f(x)=3^{x}$

$f(x)=4^{-x}$

$\displaystyle f(x)=\left( \frac{1}{2} \right)^x$

$f(x)=5^x$

指数函数的特征

指数函数具有以下性质：

指数函数的定义域由实数组成，换句话说，对于任何x值都存在指数函数。

$\text{Dom } f=\mathbff{R}$

然而，该函数只取正值，因此指数函数的范围由正实数组成。

$\text{Im } f= (0,+\infty)$

每个指数函数既是连续函数又是单射函数。

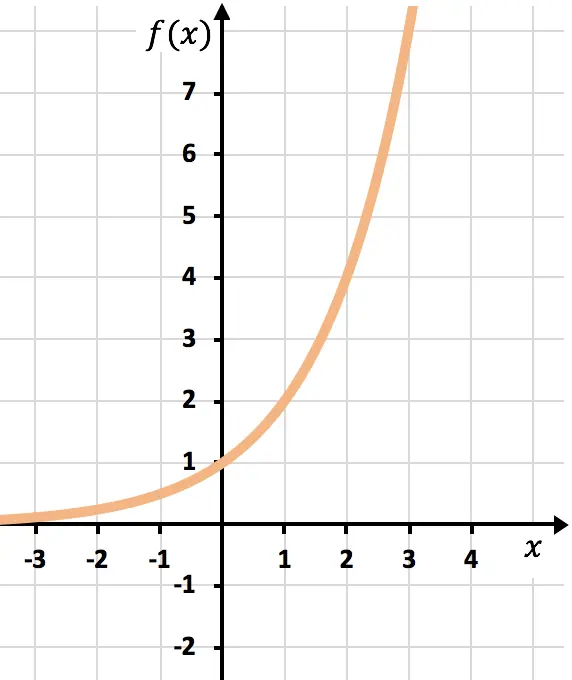
如果函数不平移，则任何指数函数都会经过点 (0,1)。因为计算为零的函数总是给出一。

$f(0)=a^0=1$

类似地，指数函数在 x=1 处的值等于底数。

$f(1)=a^1=a$

如果电源底座
$(a)$

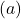
大于1，指数函数递增。另一方面，如果系数

$a$

在 0 和 1 之间，指数函数是递减的。

一般来说，x 轴是指数函数的水平渐近线。

指数函数的反函数是对数函数。因此，如果指数函数和对数函数具有相同的底，则它们的图形关于直线 y=x 对称。

如何绘制指数函数的图形

指数函数的表示非常简单。因此，让我们通过示例了解如何在图表上绘制指数函数。

在图上绘制以下指数函数：

$f(x)=2^x$

在指数函数中，不需要计算定义域，因为它们始终都是实数：

$\text{Dom } f = \mathbb{R}$

因此，制定价值表就足够了。由于这些类型的函数从一个点到另一个点变化很大，我们将计算 5 个点。但是我们计算的点越多，函数的表示就越精确。

$x= 0 \ \longrightarrow \ f(0)=2^0= 1$

$x= 1 \ \longrightarrow \ f(1)=2^1= 2$

$x= 2 \ \longrightarrow \ f(2)=2^2= 4$

$x= -1 \ \longrightarrow \ f(-1)=2^{-1}= 0,5$

$x= -2 \ \longrightarrow \ f(-2)=2^{-2}= 0,25$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 4 \\ -1 & 0,5 \\ -2 & 0,25 \end{array}$

我们建议使用计算器来查找数值表中的点，因为手动计算这些点很复杂。

现在我们在图表上表示点：

最后，我们连接点并扩展函数：

如何表示或绘制指数函数的图表

请注意，右侧的函数继续增长直至无穷大。

相反，左边的函数减少但永远不会达到 0。即使它非常接近它，它也永远不会触及它。这意味着线 y=0（x 轴）是水平渐近线。

解答了指数函数的练习

练习1

绘制以下指数函数的图形：

$f(x)= 2^x+1$

查看解决方案

它是一个指数函数，因此要表示它，您必须创建一个值表，为变量 x 赋予值：

$x= 0 \ \longrightarrow \ f(0)= 2^0+1=2$

$x= 1 \ \longrightarrow \ f(1)= 2^1+1=3$

$x= 2 \ \longrightarrow \ f(2)= 2^2+1=5$

$x= -1 \ \longrightarrow \ f(-1)= 2^{-1}+1=1,5$

$x= -2 \ \longrightarrow \ f(-2)= 2^{-2}+1=1,25$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ 2 & 5 \\ -1 & 1,5 \\ -2 & 1,25 \end{array}$

一旦我们有了数值表，我们就可以在图表上绘制获得的点并绘制函数：

逐步解决指数函数的练习

请注意，右侧的函数继续增长直至无穷大。另一方面，在左侧，函数减小但从未超过 1。实际上，函数在右侧 y=1 处有一条水平渐近线。

在这种情况下，水平渐近线位于 y=1 而不是 OX 轴，因为已经朝着函数向上垂直平移了一个单位。

练习2

在图上绘制以下指数函数：

$\displaystyle f(x)= \left(\frac{1}{3}\right)^x$

查看解决方案

它是一个指数函数，因此要以图形方式表示它，您必须构造一个值表，为变量 x 赋予值：

$x= 0 \ \longrightarrow \ f(0)= \left(\cfrac{1}{3}\right)^0 = 1$

$x= 1 \ \longrightarrow \ f(1)= \left(\cfrac{1}{3}\right)^1 = 0,33$

$x= 2 \ \longrightarrow \ f(2)= \left(\cfrac{1}{3}\right)^2 = 0,11$

$x= -1 \ \longrightarrow \ f(-1)= \left(\cfrac{1}{3}\right)^{-1} = 3$

$x= -2 \ \longrightarrow \ f(-2)= \left(\cfrac{1}{3}\right)^{-2} = 9$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 0,33 \\ 2 & 0,11 \\ -1 & 3 \\ -2 & 9 \end{array}$

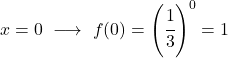
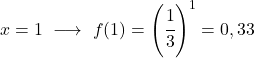
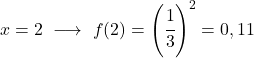
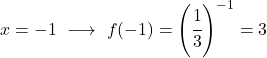
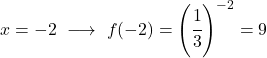
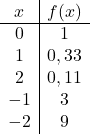
一旦我们有了数值表，我们就可以在图表上绘制计算点并绘制函数：

解决指数函数练习

请注意，左侧的函数继续增长直至无穷大。另一方面，在右侧，函数减小但从未超过 0。实际上，函数在 y=0（X 轴）处有一条水平渐近线。

练习3

在图上绘制以下指数函数：

$\displaystyle f(x)= \left(\frac{1}{2}\right)^x+3$

查看解决方案

它是一个指数函数，因此要绘制它，您必须创建一个值表，在几个点上评估该函数：

$x= 0 \ \longrightarrow \ f(0)= \left(\cfrac{1}{2}\right)^0+3 = 4$

$x= 1 \ \longrightarrow \ f(1)= \left(\cfrac{1}{2}\right)^1+3 = 3,5$

$x= 2 \ \longrightarrow \ f(2)= \left(\cfrac{1}{2}\right)^2+3 = 3,25$

$x= -1 \ \longrightarrow \ f(-1)= \left(\cfrac{1}{2}\right)^{-1}+3 = 5$

$x= -2 \ \longrightarrow \ f(-2)= \left(\cfrac{1}{2}\right)^{-2}+3 = 7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 4 \\ 1 & 3,5 \\ 2 & 3,25 \\ -1 & 5 \\ -2 & 7 \end{array}$

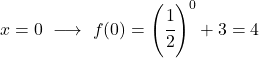
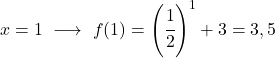
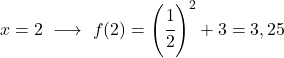
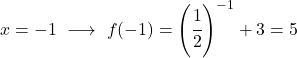
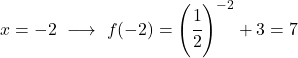
最后，我们将获得的点表示在图上并绘制函数：

指数函数问题

请注意，左边的函数无限增长到无穷大。另一方面，在右侧，函数减小但从未超过 3。实际上，函数在 y=3 处有水平渐近线。

在本例中，水平渐近线位于 y=3 而不是 X 轴，因为函数已垂直向上移动了三个单位。

练习4

解决以下有关指数函数的问题。

确定的值
$k$

使得下一个指数函数通过点(2.8)。

$f(x)=k\cdot 2^x$

查看解决方案

函数必须经过点(2,8)，因此我们可以将该点的x和f(x)的值代入函数中求得常数k的值：

$f(x)=k\cdot 2^x \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 8} \ 8 = k \cdot 2^2$

现在我们求解所得方程：

$8 = k \cdot 2^2$

$8 = k \cdot 4$

$\cfrac{8}{4} = k$

$\bm{ 2 = k}$

练习5

解决以下有关指数函数的问题。

白蚁种群根据以下功能进行繁殖：

$f(t)=3^{t+1}$

金子

$f(t)$

是白蚁的数量，

$t$

时间已经过去几个月了。

1年后会有多少白蚁？

查看解决方案

要计算一年内白蚁的数量，只需将经过的时间（1 年）代入函数即可。但由于函数t是经过的月份而不是年份，因此我们必须将t =12，因为一年有 12 个月：

$f(t)=3^{t+1}$

$f(12)=3^{12+1}$

$f(12)=3^{13}$

我们用计算器求解：

$f(12)= 1594323$

所以一年后将会有 1,594,323 只白蚁。

发表评论取消回复