方程组是两个或多个具有多个未知数的方程组。因此,为了求解系统,我们可以使用四种方法:替换、均衡、归约和作图。但是,在开始解释解决方案之前,我们将根据解决方案的数量来定义存在的系统类型:
- 确定兼容系统:它只有一个解,可以用两条相交于一点(即解)的直线来表示。
- 不定兼容系统:它有无限个解,这是因为有两条直线在同一点重合。
- 不兼容系统:它没有解决方案,因为线是平行的,因此没有共同点。
求解线性方程组的方法
我们现在将解释可用于求解方程组的不同系统。在解释中,您会找到理论和一些示例,因此所有解释的概念都会更加清晰。请注意,在本文中我们将仅讨论2×2 方程组,这意味着我们将简单地处理由两个方程组成的系统。也就是说,让我们从解释开始。
替代法
代入法是将其中一个方程中的一个未知数分离出来,然后将得到的表达式代入相反的方程中。当至少一个未知数的系数值等于 1 时,最推荐使用此方法。因此,遵循的步骤非常简单:
- 从两个方程之一中分离出一个未知量。
- 将与我们从第一个方程中消除的未知数等效的表达式代入另一个方程。
- 删除我们得到的方程中相反的未知数。
- 一旦我们获得了第一个变量的值,我们就需要用它来查找第二个变量。
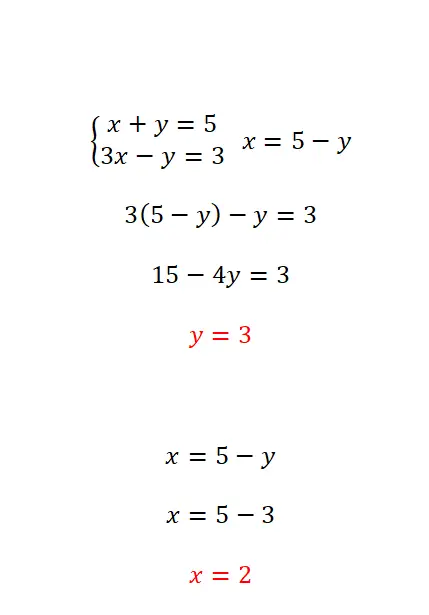
均衡法
匹配方法包括隔离两个方程中的相同变量,然后匹配获得的两个表达式。当可以在两个方程中轻松分离相同的未知数时,建议使用此方法,因为它使整个计算更容易。在这种情况下,您必须遵循的程序如下:
- 我们隔离在两个方程中选择的未知数。
- 我们将等价的表达式同化为这个未知数。
- 我们正常解方程。
- 我们用我们计算的值来计算另一个未知数。
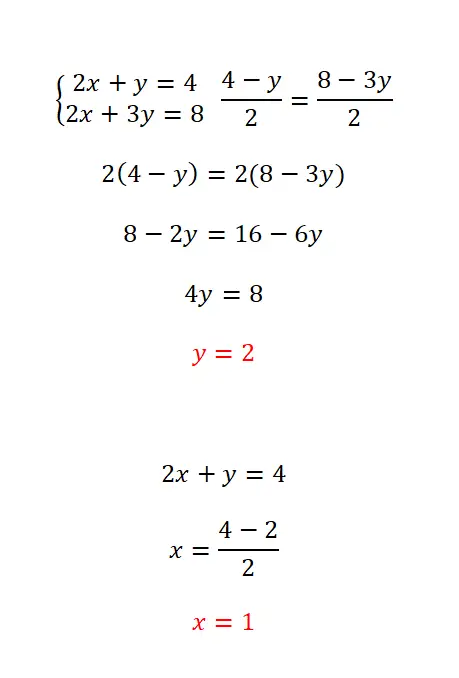
还原法
归约方法基于将两个方程乘以两个数字,这使我们能够获得两个表达式中变量之一具有不同符号的相同系数。当相同的未知数在所有方程中具有相同的系数或具有相同的符号相反的系数时,最推荐使用此方法。解决过程如下:
- 将两个方程乘以必要的数字(您必须找到两个数字,使得两个方程中的两个变量之一能够获得相同的系数,但符号相反)。
- 然后将方程相减或相加,以消除该未知数及其各自的系数。
- 然后求解剩余方程。
- 我们使用这个方程的结果来获得另一个变量中缺少的数值。
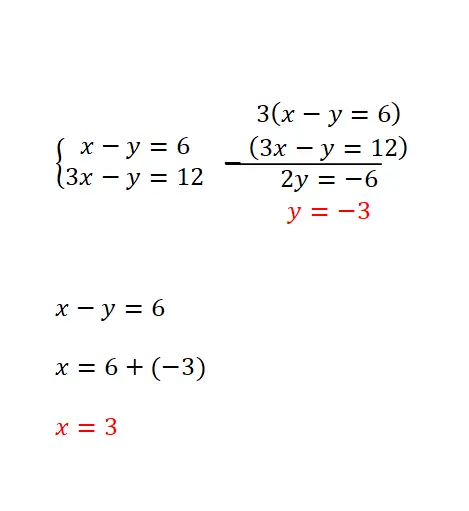
图解法
最后,我们可以选择通过图形表示来求解方程组。这种方法与其他方法有很大不同,因为它没有复杂的数学部分,它几乎完全是图形化的。因此,要知道未知数的值,我们必须以直线方程的形式构造两个方程: y = mx + b 。这样我们就能够进行表示,然后我们将两个函数之间的分割点的坐标值与未知数相关联。这是一个有效的例子:
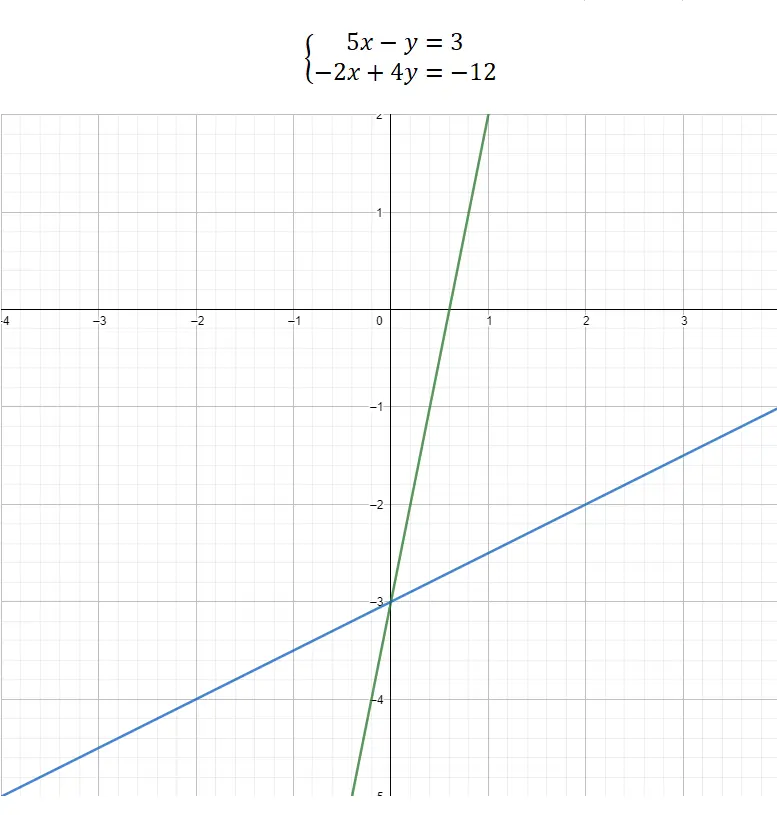
从图中可以看出,两个函数之间的分界点是 (0, -3)。因此,x 的值 = 0,y 的值 = -3。这就是方程组的图形解法。
如何求解二次方程组?
为了求解二次方程组,我们可以使用刚才讨论的方法。就我个人而言,我们喜欢推荐替换法,因为它可以让我们快速获得具有单个未知数的方程。另一方面,如果我们使用归约或均衡方法,计算就会变得相当复杂。因此,一旦替换两个变量之一,您只需求解所得的二次方程或二次方程。这是一个示例,以便您可以看到整个过程:
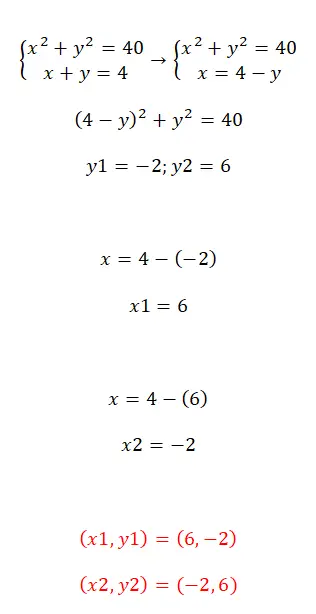
求解方程组的练习
我们现在为您提供一些关于线性和二次方程组的练习,以便您可以应用所解释的理论。这样您将更好地理解与计算方程组相关的所有概念。我们建议您在查看我们提供的答案之前先尝试解决这些问题,这样您就能从练习中获得最大收益:
练习1
使用代换法求解该方程组:
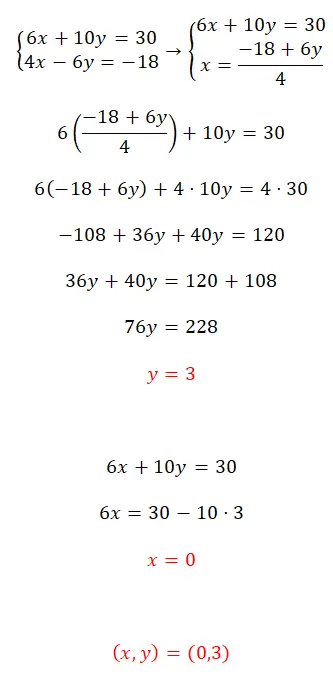
- 我们首先分离方程中的两个未知数之一。
- 然后,我们将在相反方程中获得的表达式替换为我们之前求解的未知数。
- 然后我们得到相反变量的结果。
- 接下来,我们将第一个发现的值代入两个方程之一来计算第一个未知数的值。
- 最后,我们表达两个变量的结果。
练习2
使用代换法求解该方程组:
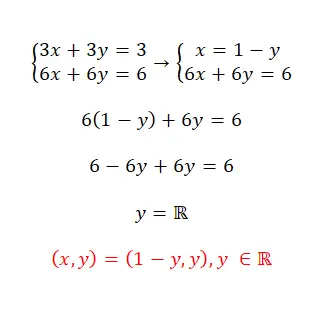
- 在这种情况下,我们将遵循相同的过程:隔离一个未知数,将其替换为另一个表达式并隔离第二个变量。
- 正如我们所看到的,这是一个不确定兼容系统,因为它有无限多个解。
练习3
使用均衡方法求解该方程组:
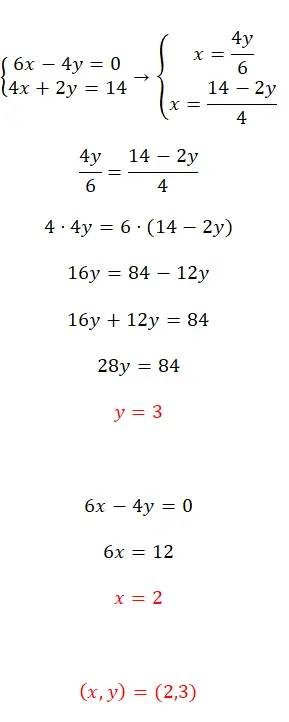
- 第一步是隔离两个方程中的相同变量,在本例中我们选择了 x。
- 然后我们匹配结果表达式并开始求解。
- 这样,我们就得到了第一个未知数的值。
- 如果我们将其代入两个原始方程之一,我们就可以计算出第二个未知数。
- 最后,我们表达两个变量的结果。
练习4
使用均衡方法求解该方程组:
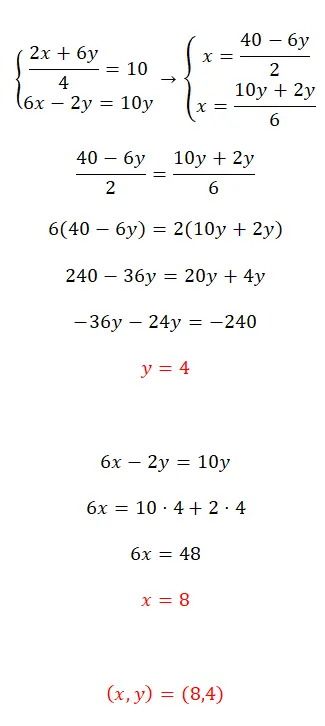
- 首先,我们分离两个方程中的 x。
- 接下来,我们匹配我们获得的表达式。
- 我们得到第一个未知数的值。
- 我们将该值代入两个初始方程之一并计算第二个未知数。
- 最后,我们表达了两个陌生人的价值。
练习5
使用归约法求解该方程组:
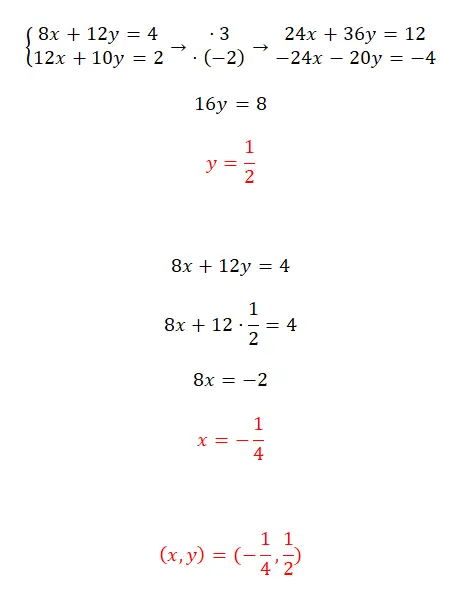
- 您必须寻找两个数字,使两个方程中的两个变量之一能够获得相同的系数,但符号相反。
- 然后,简单地求解通过将获得的两个表达式相加而获得的方程。
- 接下来,我们将 y 代入两个原始方程之一,以计算 x。
- 最后,我们表达了系统的结果。
练习6
使用归约法求解该方程组:
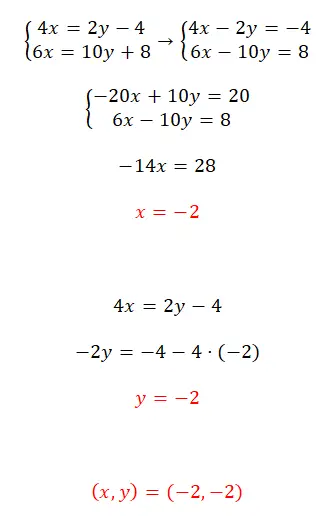
- 我们首先排列方程(将所有变量传递到左侧)。
- 然后我们将第一个方程乘以-5。
- 我们求解通过将两个方程相加得到的方程并获得 x 的值。
- 我们使用这个已知值来获得 y 的值。
- 我们表达方程组的结果。
练习7
使用代换法求解该方程组:
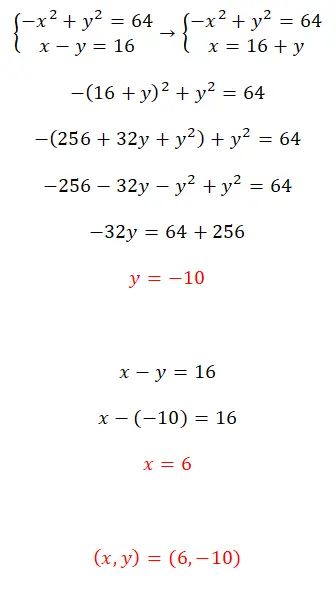
- 为了求解这个非线性方程组,我们建议使用替换法。
- 因此,您可以使用相当于 x 的表达式构造一个方程。
- 您获得未知 y 的值。
- 您可以使用之前计算的值来计算 x 的值。
- 而且你已经拥有这两种价值观。
练习8
使用您选择的方法求解该方程组:
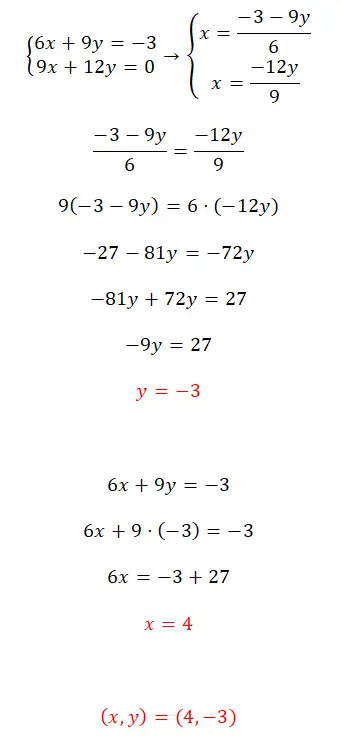
- 在这种情况下,我们会遇到一个确定的兼容系统,我们将使用均衡方法来解决它。
- 因此,我们求解两个方程中的 x 并将两个结果表达式设置为相等。
- 解方程后,我们得到y的值。
- 我们用这个值来求 x 的值。
- 最后,我们表达了系统的结果。