在这里您可以找到所有类型的著名身份(或著名产品)的解析说明。您将能够看到所有著名恒等式的公式是什么,以及逐步解决的示例和练习。此外,我们还将向您展示这些著名的数学规则的用途。
👉👉 下面我们将逐步解释每个值得注意的等式,但如果您愿意,可以直接转到表格😉,其中总结了所有公式。 👈👈
什么是显着身份(或显着产品)?
显着恒等式,也称为显着乘积或显着等式,是允许直接求解多项式运算的数学规则。
最常见的值得注意的恒等公式是和的平方、差(或减法)的平方以及和乘以差。

但下面我们不仅会教您如何计算这些显着乘积,还会向您展示所有存在的显着恒等式类型。
著名的恒等公式(或乘积)
一旦我们了解了显着乘积(或显着等式)的定义,我们就会看到显着恒等式的公式是什么。另一方面,如果您对公式演示感兴趣,您可以通过单击“查看演示”按钮来查看它们的公式。
总和的平方
总和的平方或平方和是主要的显着恒等式之一。更准确地说,它是一个有两个正项的2次方的二项式,也就是说它的代数表达式是(a+b) 2 。
因此,总和的平方公式为:

如果我们从一个升到 2 的正二项式开始:
![]()
从数学上讲,上面的平方相当于因子
![]()
乘以自身:
![]()
因此,我们使用分配律来乘多项式:
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c871c4ad6546c817128379acbef78c8_l3.png)
在获得的四项中,
![]()
和
![]()
看起来很相似,所以我们可以将它们分组:
![]()
如此之多以至于我们已经得出了平方和公式的表达式,并为此推导了它:
![]()
出于好奇,这种卓越产品的表达方式被称为完美平方三项式。
因此,总和的平方等于第一项的平方,加上第一项与第二项乘积的两倍,再加上第二项的平方。
因此,要求解平方和,仅对两者进行每次加法运算是不够的,此外,两个加法必须彼此相乘并乘以 2。记住这一点很重要,因为这种类型的一个非常典型的错误产品 忘记这个术语是很值得注意的。

例子:
- 通过应用相应的公式计算以下显着恒等式:
![]()
正如我们刚刚看到的,平方和显着相等的公式是:
![]()
因此,我们首先要确定参数
![]()
和
![]()
的公式。在这种情况下,
![]()
代表
![]()
的对和
![]()
对应数字5:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5ba75b0f34f956985ea0163011a03acf_l3.png)
那么,现在我们知道了
![]()
和的
![]()
我们可以使用平方正二项式的公式来求出结果:

差的平方
差的平方或差的平方 是 3 个最常用的著名恒等式中的另一个。特别地,它对应于由一个正项和另一个负项升到2形成的二项式,也就是说它的代数表达式是(ab) 2 。
因此,差的平方(或减法的平方)的公式如下:

根据平方减法的二项式表达式:
![]()
显然,之前的幂等于因子的乘积
![]()
乘以自身:
![]()
现在我们应用分配律将两个括号相乘:
![Rendered by QuickLaTeX.com \begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b46073fd758d93fff8956f0a8dd57af_l3.png)
因此,您只需将相似的术语组合在一起即可完成公式检查:
![]()
然后用数学方法证明差平方的公式:
![]()
因此,差值的平方等于第一项的平方,减去第一项与第二项乘积的两倍,再加上第二项的平方。
至于平方和显着相等,我们一定不要忘记加上公式的中间项,因为下面的等式是不正确的:

例子:
- 求解以下显着的平方差等式:
![]()
它是平方减法的显着乘积,因此有必要应用其相应的公式:
![]()
接下来,我们必须确定未知数的值是什么。
![]()
和
![]()
的公式。在这种情况下,
![]()
是变量
![]()
和
![]()
对应数字3:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1bb2d14a30d2cdabae6458f5df32392a_l3.png)
请注意,负号不是参数的一部分
![]()
但您必须始终采用不带符号的数字才能正确应用此公式。
因此我们已经知道了
![]()
和的
![]()
,因此将这些值代入公式中就足以解析显着恒等式:

差和
和与差的乘积是最常用的 3 个恒等式之一。顾名思义,它是一个正二项式乘以它的共轭二项式(同样的二项式但中间符号改变了),也就是说这类显着乘积的代数表达式是(a+b)·(ab) 。
和与差的乘积的显着恒等式的公式如下:

从总和与任意两项相减的乘积开始:
![]()
为了演示该公式,我们只需使用分配律将第一个括号乘以第二个括号即可:
![Rendered by QuickLaTeX.com \begin{array}{l}(a+b)\cdot (a-b)= \\[2ex] = a\cdot a +a\cdot (-b) +b \cdot a +b\cdot (-b) =\\[2ex] = a^2 -ab+ba-b^2\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-346d3d7ca4da1e71fad52c84a33ef4fc_l3.png)
现在我们将相似的术语组合在一起:
![]()
我们因此实现了非凡的平等。因此,证明了这种非凡的身份类型的公式:
![]()
因此,两个量的和与差的乘积等于这些量的平方差。或者换句话说,将两项不同项的和相乘并减去这两项相同的项相当于对两项进行平方并减去它们。
例子:
- 使用相应的公式,找到以下两个不同项之差之和的显着乘积:
![]()
正如我们在上面看到的,和乘以差的显着相等的公式如下:
![]()
首先我们需要做的是识别字母的值
![]()
和
![]()
的公式。在这种情况下
![]()
对应变量
![]()
和
![]()
对应数字2。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)\cdot (a-b) \\[2ex] (x+2)\cdot (x-2) \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-87b76b09924467ba75f033336e6a18e5_l3.png)
当我们已经知道参数取什么值时
![]()
和
![]()
我们应用总和与差的乘积公式:
三项式的平方
三项式(由 3 项组成的多项式)的平方等于第一项的平方,加上第二项的平方,加上第三项的平方,加上第一项的两倍和第二项的两倍,加上第一项的两倍到第三个,再加上第二个的两倍作为第三个。

从任何三项式的平方:
![]()
上面的平方可以分解为三项式与其自身的乘积:
![]()
现在我们求解多项式乘法:
![]()
最后,我们将类似的术语分组:
![]()
这样,我们就已经得到了公式的表达,于是三项式的平方公式就得到了证明:
![]()
例子:
- 找到以下显着的等式:
![]()
三项式平方的公式为:
![]()
与所有值得注意的等式一样,您必须首先确定公式中未知数的值。在这个练习中
![]()
东方
![]()
系数
![]()
对应于
![]()
和
![]()
是独立项 3:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2+x+3\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=x \\[2ex] c=3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55e06f44486e75e9153a60d36e83bc37_l3.png)
当我们已经知道这些值时,只需将这些值代入公式并进行计算:

著名身份(或产品)的立方
我们刚刚研究了所有显着恒等式的平方,即由 2 次幂形成的所有类型的显着恒等式。那么,现在我们要分析显着恒等式的立方。当然,立方恒等公式稍微复杂一些,但也非常有用。
总和的立方
值得注意的和的立方积是一个 3 次方的二项式(只有两个单项式的多项式),其两个元素为正。因此,在代数上,总和的立方表示为(a+b) 3 。
和的立方显着相等的公式是:

从正二项式立方开始:
![]()
上述功率可以分解为因子的乘积
![]()
按其平方:
![]()
同样,正如我们在著名的平方方程中看到的那样,二项式
![]()
可以用总和的平方公式来求解:
![]()
然后我们将两个多项式相乘:
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a^2+2ab+b^2) & = a\cdot a^2 +a\cdot 2ab + a\cdot b^2+b\cdot a^2 +b\cdot 2ab +b \cdot b^2 \\[2ex] & = a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-06771ecbb13542eae2a68477f849d729_l3.png)
最后,我们只需将相似的术语组合在一起:
![]()
从而验证了二项式和立方的显着恒等式的公式:
![]()
简而言之,加到 3 的和等于第一个的立方,加上第一个的平方的三倍乘以第二个,再加上第一个的三倍乘以第二个的平方,再加上第二个的立方。
例子:
- 使用相应的公式求解以下立方和的显式恒等式:
![]()
在这个问题中,我们有一个 3 次方的二项式,其两项均为正。因此,我们必须使用立方和的公式:
![]()
我们现在需要找到参数的值
![]()
和
![]()
的公式。在这种情况下,
![]()
对应变量
![]()
和
![]()
是 2 号。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^3\\[2ex] (x+2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-909b3b4a2f976c165f160a6765b3ed9d_l3.png)
我们通过替换以下值来计算显着产品
![]()
和的
![]()
在公式:

差异的立方体
差的立方或减法 的立方是 3 次方的二项式,其中项带负号。因此,这种非凡产品类型的数学表达式为(ab) 3 。
差值(或减法)立方的公式为:

显然,这个公式的证明与著名的立方和乘积的证明非常相似。但在这种情况下,我们从负立方二项式开始:
![]()
显然,之前的增强可以分解为因子的乘积
![]()
乘以它的平方:
![]()
因此,当我们研究著名的平方恒等式时,二项式
![]()
可以用差值平方的公式计算:
![]()
我们现在生成两个多项式的乘积:
![Rendered by QuickLaTeX.com \begin{aligned} (a-b)\cdot (a^2-2ab+b^2) & = a\cdot a^2 +a\cdot (-2ab) + a\cdot b^2-b\cdot a^2 -b\cdot (-2ab)-b \cdot b^2 \\[2ex] & = a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-627a273de8fff974f4a14a32fcee90b8_l3.png)
最后一步是将相似的术语分组:
![]()
因此,减去二项式的立方的显着恒等式的公式得到验证:
![]()
因此,差值(或减法)增加到三等于第一个的立方减去第二个的三倍第一个的平方,加上第一个的三倍乘以第二个的平方,再减去第二个的立方。
例子:
- 使用相应的公式计算下一个立方二项式(差值):
![]()
在本练习中,我们有一对具有正元素和负元素的元素。因此,我们必须使用立方差的公式:
![]()
首先,一如既往,我们确定未知数的值
![]()
和
![]()
的公式。在这种情况下
![]()
表示单项式
![]()
和
![]()
是二项式的独立项,即 2。
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^3\\[2ex] (3x-2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=3x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a792ec6dead8466ec6a2cb2a43d9fab4_l3.png)
注意参数
![]()
简单地等于 2,没有数字的负号。记住这一点对于正确应用该公式非常重要。
最后,我们通过将以下值放入其中来找到显着的身份:
![]()
和的
![]()
在公式:

著名身份汇总表
总之,我们制作了一个表格,其中列出了我们见过的所有著名身份(或产品),因此您可以更轻松地研究它们。 😉

解决了著名身份(或产品)的练习
为了让您完全理解卓越恒等式的概念,也称为卓越产品或卓越平等,我们准备了几个逐步解决的练习。你可以尝试做一下,然后检查你是否完成了练习的解决方案。
⬇⬇ 不要忘记您可以在下面的评论中向我们询问所有问题! ⬇⬇
练习1
展开以下显着恒等式(平方和):
![]()
![]()
![]()
![]()
问题中所有值得注意的恒等式都是平方和,因此在这种情况下我们必须始终应用相同的公式:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-571dada676a093b9b625887a09615b5c_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(6x+2)^2 & =(6x)^2+2\cdot 6x \cdot 2+2^2\\[2ex] & = \bm{36x^2+24x+4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-067fdf38612ca481db587bda479cab24_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-62f7ef68fc47d45958f6a10dbfe3f512_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2fdf798e7d585cdbc2bbeb0417bfc62a_l3.png)
练习2
开发以下著名产品(差异平方):
![]()
![]()
![]()
![]()
本练习中所有值得注意的乘积都是平方减法,因此我们只需要应用一个公式:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14d502eda968fe82617b4403cd9c4722_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c22d520301280872e645f5683a2fba8e_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-95c7c481a96b20b700bd2253c90f0c0d_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cea9fa89580d3d9d9df7fd93cca2b89_l3.png)
练习3
建立以下值得注意的等式(差和的乘积):
![]()
![]()
![]()
![]()
由于本练习中所有值得注意的等式都是和乘以差,因此它们都用相同的公式求解:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+5)(x-5) &=x^2-5^2\\[2ex] & = \bm{x^2-25}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-826c4aec8f005514a14cdc8555c084c4_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(2x+6)(2x-6) & =(2x)^2-6^2 \\[2ex] & = \bm{4x^2-36}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6793239af84413fb9408c2cb6033e5ce_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}(x+7)(x-7) & =x^2-7^2 \\[2ex] & = \bm{x^2-49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-630b94cf4be27c5f7b9c87651368634d_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(x-4y)(x+4y) & =(x+4y)(x-4y) \\[2ex] & =x^2-(4y)^2\\[2ex] & = \bm{x^2-16y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-80c5451e407a2c0e670c6cb22a74043c_l3.png)
练习4
解决以下所有值得注意的身份:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(x^2+10\right)\left(x^2-10\right) & =\left(x^2\right)^2-10^2\\[2ex] & = \bm{x^4-100}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c65875e01d82840e30ae85d803d45e90_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04e0bcf5df362d320cfdb2f87cdc6ddc_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2 = \\[2ex] &= \bm{36x^6-48x^3y^4+16y^8}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc3f7dc61f7c44a60c01e0a95de278fa_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}\left(8x^3+y^2\right)\left(8x^3-y^2\right) & =\left(8x^3\right)^2-\left(y^2\right)^2 \\[2ex] & = \bm{64x^6-y^4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4d4a0c86d26820881eb65cb92c3679a_l3.png)
![Rendered by QuickLaTeX.com \text{E)} \ \begin{aligned}\left(5x^2-9x\right)^2 & =\left(5x^2\right)^2-2\cdot 5x^2\cdot 9x +\left(9x\right)^2 \\[2ex] & = \bm{25x^4-90x^3+81x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-432c4ae0f050bec15e3fa52f426698ec_l3.png)
练习5
计算以下著名产品:
![]()
![]()
![]()
![]()
要找到问题的所有显着乘积,有必要根据情况应用求和和求差立方的公式:
![]()
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+4)^3& =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 4^2+4^3\\[2ex] & =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 16+64 \\[2ex] & = \bm{x^3+12x^2+48x+64}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14695fb807e2df89352fdd1c1dced2ee_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(x^2-5\right)^3& =\left(x^2\right)^3-3\cdot \left(x^2\right)^2\cdot 5 +3\cdot x^2\cdot 5^2-5^3\\[2ex] & =x^6-3\cdot x^4\cdot 5 +3\cdot x^2\cdot 25-125 \\[2ex] & = \bm{x^6-15x^4+75x^2-125}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5be0d584351feb0bef5572ca5c9e159a_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(2x-1\right)^3& =\left(2x\right)^3-3\cdot \left(2x\right)^2\cdot 1 +3\cdot 2x\cdot 1^2-1^3\\[2ex] & =8x^3-3\cdot 4x^2\cdot 1 +3\cdot 2x\cdot 1-1 \\[2ex] & = \bm{8x^3-12x^2+6x-1}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f44f9c3283dad97321644c6e559f64ff_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+2)^3& =(5x)^3+3\cdot \left(5x\right)^2\cdot 2 +3\cdot 5x\cdot 2^2+2^3\\[2ex] & =125x^3+3\cdot 25x^2\cdot 2 +3\cdot 5x\cdot 4+8 \\[2ex] & = \bm{125x^3+150x^2+60x+8}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-156e7619e4d6ef129f04250af8197d2e_l3.png)
练习6
解决以下值得注意的等式:
![]()
![]()
![]()
![]()
为了求解所有这些值得注意的恒等式,我们需要使用三项式的平方公式,即:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{array}{l} \left(x^2+x+5\right)^2 = \\[2ex] = \left(x^2\right)^2+x^2+5^2+2\cdot x^2 \cdot x + 2 \cdot x^2 \cdot 5 +2 \cdot x \cdot 5 = \\[2ex] = x^4+x^2+25+2x^3 + 10x^2 +10x = \\[2ex] = \bm{x^4+2x^3+11x^2+10x+25} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-749dc45e7a00d7122d62b774706bdcc0_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{array}{l}\left(x^2+3x-4\right)^2 = \\[2ex] = \left(x^2\right)^2+(3x)^2+(-4)^2+2\cdot x^2 \cdot 3x + 2 \cdot x^2 \cdot (-4) +2 \cdot 3x \cdot (-4) = \\[2ex] = x^4+9x^2+16+6x^3-8x^2-24x = \\[2ex] = \bm{x^4+6x^3+x^2-24x+16} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1f51f18b3c1118b6e8e3acc3441b0ec_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{array}{l}\left(4x^2-6x+3\right)^2 = \\[2ex] = \left(4x^2\right)^2+(-6x)^2+3^2+2\cdot 4x^2 \cdot (-6x) + 2 \cdot 4x^2 \cdot 3 +2 \cdot (-6x) \cdot 3 = \\[2ex] = 16x^4+36x^2+9-48x^3+24x^2-36x = \\[2ex] = \bm{16x^4-48x^3+60x^2-36x+9} \end{array}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-49c6496bf684296d315fc96d9cb5857e_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{array}{l} \left(x^3-3x^2-9x\right)^2 = \\[2ex] = \left(x^3\right)^2+\left(-3x^2\right)^2+(-9x)^2+2\cdot x^3 \cdot (-3x^2) + 2 \cdot x^3 \cdot (-9x) +2 \cdot (-3x^2) \cdot (-9x) = \\[2ex] = x^6+9x^4+81x^2-6x^5-18x^4+54x^3 = \\[2ex] = \bm{x^6-6x^5-9x^4+54x^3+81x^2} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7cd08035d8402c27c411bcf5b30216cb_l3.png)
练习7
计算以下带有根和分数的显着恒等式(高难度):
![]()
![]()
![]()
![]()
A) 部分由平方减法组成,因此要解决它,必须应用其相应的公式,此外,必须记住,如果根是平方的,则它会被简化:
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-999e71bf062ea313780439abaf2b4295_l3.png)
B) 部分涉及减法加法,单项式具有分数系数,必须使用减法加法公式和分数的性质来确定这个值得注意的乘积:
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right) & \displaystyle =\left(\frac{1}{2}x^2\right)^2-\left(\frac{5}{3}x\right)^2\\[4ex] \displaystyle & =\frac{1^2}{2^2}x^4-\frac{5^2}{3^2}x^2\\[4ex]\displaystyle & = \mathbf{\frac{1}{4}}\bm{x^4-}\mathbf{\frac{25}{9}}\bm{x^2} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-24593bac7bd4a9837e1f18fef4f9c38e_l3.png)
C) 节中值得注意的等式是求和到 2,并且同样由分数组成。因此,为了计算它,我们需要使用平方和的公式加上分数的性质:
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c50dcca740e334b34f746e71f4af826e_l3.png)
最后一个值得注意的恒等式涉及无理系数的和乘以差,因此我们应用和乘以差的公式,然后简化平方根:
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}\Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr) & =\Bigl(9x^3\Bigr)^2-\left(\sqrt{5x}\right)^2\\[2ex] & = \bm{81x^6-5x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c540e4315e9e84faaa2ff656c4eec21_l3.png)
其他值得注意的身份类型
我们上面讨论的所有值得注意的身份都是最常用的。然而,在数学中,还有其他值得注意的产品类型也值得了解,因为它们用于不同的目的。
立方和
立方之和对应于一个二项式,其两项均为正,而且其立方根是精确的。因此,立方和的代数表达式为a 3 +b 3 。

这个值得注意的乘积的公式用于分解多项式,也就是说,通过该公式,我们将多项式转换为二项式与三项式的乘积。
所以您可以看到它是如何完成的,下面是这个非凡身份的示例应用程序:
![]()
事实上,前面的表达式由立方相加组成,因为单项式的立方根
![]()
是精确的(不给出小数)并且数字 8 也是:
![]()
![]()
![]()
因此,我们可以利用完美立方和的公式将三次表达式转换为二项式与三项式的乘积:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} x^3 +2^3 & = (x+2)(x^2-x \cdot 2 + 2^2) \\[2ex] & = (x+2)(x^2-2x + 4) \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f30ea5f0f7ef1b89a16f1d00e54d063c_l3.png)
立方体的差异
立方的差(或减)是由一个正项和一个负项组成的二项式,其立方根是精确的。换句话说,立方差以a 3 -b 3的形式表达。

让我们举个例子,以便您了解如何解析这种非凡的身份类型:
![]()
这是立方差,因为单项式的立方根
![]()
27 是正确的:
![]()
![]()
![]()
因此,您可以使用完美立方差的公式来分解二项式:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} x^3 -3^3 & = (x-3)(x^2+x \cdot 3 + 3^2) \\[2ex] & =(x-3)(x^2+3x + 9) \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-342a448f849bf2856ad9a5394733faeb_l3.png)
具有共同项的二项式的乘积
这个著名的乘积用于将具有共同项的两个二项式的乘积转换为二次多项式。

以下是此类卓越产品的详细示例:
![Rendered by QuickLaTeX.com \begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8447db6a2246c09b2e7be29f8050a3d6_l3.png)
更多身份
虽然著名的身份是最有名的,因为它们是最常见的,但应该注意的是,还有更多其他名字的身份。如果您好奇的话,这里列出了其他鲜为人知的身份:
- 拉格朗日恒等式:
-
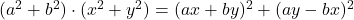
-
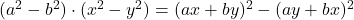
- 勒让德恒等式:
-
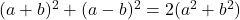
-
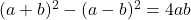
-
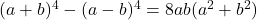
- 阿尔甘德身份:
-
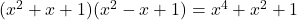
- 高斯恒等式:
-
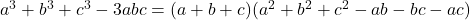
-
![Rendered by QuickLaTeX.com a^3+b^3+c^3-3abc= \frac{1}{2} (a+b+c)\left[(a-b)^2+(b-c)^2+(a-c)^2\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6b2da7d99ade85355a54bee45b79a9f_l3.png)
著名的身份识别应用程序
如果您已经完成了这一步,则意味着您已经知道如何使用显着恒等式进行计算。明亮的!但说实话……显赫的身份有什么用呢?何时使用显着身份?
正如我们在整篇文章中所看到的,显着恒等式的主要目的是简化计算。也就是说,借助卓越的产品,我们可以直接求解复杂多项式的某些幂,而无需进行困难的运算。
但值得注意的等式还具有其他功能,例如多项式因式分解和平方完成。然后我们将了解每个应用程序的组成。
多项式因式分解
一些非常特定类型的多项式可以用显着的恒等式进行因式分解。例如,如果我们找到一个由两个完全平方项组成的多项式(它们的平方根是精确的),我们可以使用和乘以差的显着等式公式对它进行因式分解:
![]()
![]()
同样,遵循加法或减法平方显着恒等式的三项式可以因式分解:
![]()
![]()
![]()
![]()
同样,一旦多项式被分解,就可以找到该多项式的根(或零点)。即便如此,这个概念理解起来还是有点复杂,所以如果您更感兴趣,我们建议您在我们网站(右上角)的搜索引擎中搜索解释,因为我们有整篇文章解释它。
方形完成
平方完成是一种数学过程,用于将二次三项式转换为平方加(或减)数字的和。
给定任意三项式:
![]()
那么三项式可以转化为下面的表达式:
![]()
其中参数
![]()
和
![]()
由以下公式计算:
![]()
即使您看起来不像,这两个公式也是从显着的恒等式推导出来的。因此,由于出色的产品,这些正方形才得以完成。
作为示例,我们将将此过程应用于以下三项式:
![]()
我们计算参数
![]()
和
![]()
![]()
![]()
因此,多项式仍然是:
![]()