在这里你会发现恒等函数是什么。此外,您将能够了解如何以图形方式表示恒等函数及其特征。
什么是恒等函数?
恒等函数是指与参数具有相同值的函数。恒等函数可以用术语id来表示。
因此,恒等函数的数学表达式为:
![]()
例如,x=1 的恒等函数图像值为 1,x=2 的图像值为 2,x=3 的图像值为 3,…
![Rendered by QuickLaTeX.com \begin{array}{c}f(1)=1\\[2ex]f(2)=2\\[2ex]f(3)=3\\ \bm{\vdots}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b85e48e3f36d1eb4271b265aaf35bef_l3.png)
恒等函数是线性函数的一个示例。在以下链接中,您可以看到此类函数的更多示例:
➤请参阅:线性函数的示例
恒等函数的图形表示
恒等函数的图形对应于第一象限和第三象限的平分线。
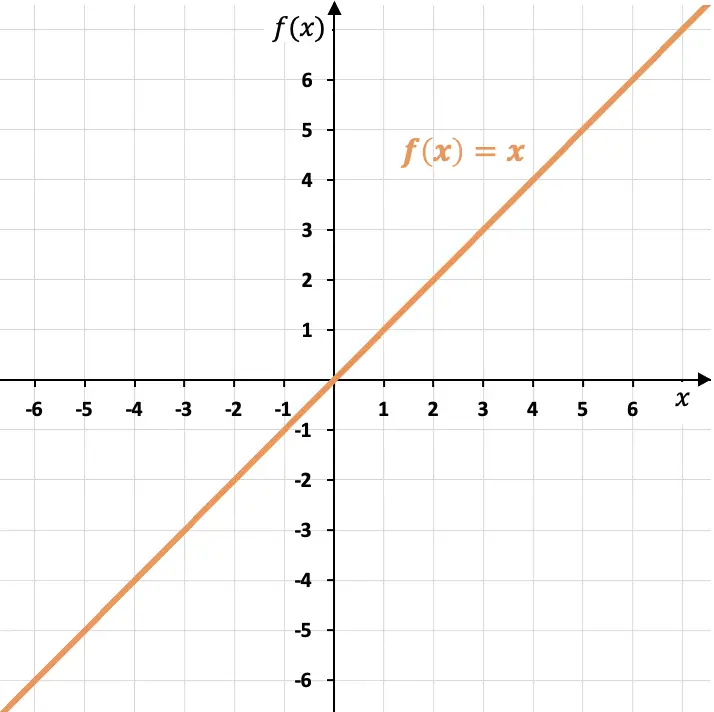
正如您所看到的,恒等函数穿过坐标原点(点 (0,0)),并且斜率等于 1 (m=1),因为变量的一个单位会增加,并且对于独立函数的每个值变量 X。此外,恒等函数与 X 轴形成 45° 角。
恒等函数的特点
恒等函数具有以下性质:
- 恒等函数的定义域都是实数:
![]()
- 恒等函数的值域(或范围)也由所有实数组成:
![]()
- 恒等函数是连续的双射函数。
- 此外,恒等函数由奇函数组成,这意味着它是关于坐标原点的对称函数。
![]()
➤参见: 奇对称函数
- 恒等函数在其整个域内递增,其斜率等于 1。
![]()
- x 轴(OX 轴)和 y 轴(Y 轴)交于同一点:坐标原点。
![]()
- 它可以归类为一次多项式函数。
- 恒等函数充当函数组合的中性元素。因此,任何由恒等函数组成的函数都会产生函数本身。
![]()
- 价值
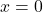
是此类函数的唯一根。
- 当 x 趋于正无穷大或负无穷大时,恒等函数的极限分别给出正无穷大和负无穷大:
![]()
![]()
- 因此恒等函数没有渐近线。
- 恒等函数的导数是值为 1 的常数函数:
![]()
- 恒等函数的积分是二次函数:
![]()
➤请参阅:二次函数的公式