在本文中,您将找到维尔斯特拉斯定理的定义。此外,您还可以通过逐步解决维尔斯特拉斯定理的几个练习来进行练习,以完美地理解它。
维尔斯特拉斯定理的陈述
维尔斯特拉斯定理指出,如果函数在闭区间上连续,则该函数在该区间上具有绝对最大值和绝对最小值。
➤请参阅: 什么是连续函数?
维尔斯特拉斯定理只指出存在最大值和最小值,但计算这些点的值并没有什么用处。
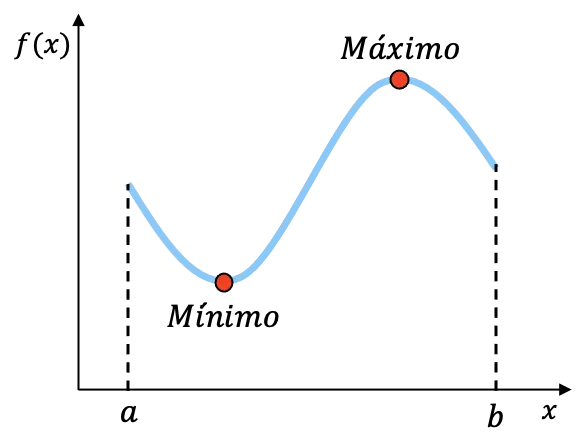
例如,上面绘制的函数在区间 [a,b] 上是连续的,并且在此区间上具有最小值和最大值。虽然我们无法知道这两点的准确坐标,但我们知道函数在区间内有这两个端点。
➤请参阅: 如何计算函数的最大值和最小值
由于该函数在整个区间内是连续的,这意味着它还将在同一区间内取绝对最小值和绝对最大值之间的所有可能值。
此外,根据维尔斯特拉斯定理,我们可以推断出闭区间上的任何连续函数都在的上方和下方有界,并且函数的上限和下限分别是绝对最大值和最小值。
在数学上,维尔斯特拉斯定理可以表达如下:
![]()
金子
![]()
和
![]()
是闭区间中包含的两个点(分别是绝对最小值和绝对最大值)
![]()
其中定义了该函数。
维尔斯特拉斯定理的证明相当复杂,对概念的贡献不大,所以本文不做解释。重要的是你要了解维尔斯特拉斯定理是什么以及它的用途。
维尔斯特拉斯定理解决的问题
练习1
确定以下函数是否有界于建议的区间:
![]()
➤请参阅:对数函数的域
我们可以通过应用 Weierstrass 定理来确定函数是否在区间 [5,10] 上有界。因此,我们必须知道函数在此区间内是否连续,为此,我们计算对数函数的域:
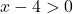
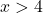
![]()
该函数对于所有大于x=4的值都是连续的,因此它在区间[5,10]上连续。
因此,该函数满足区间 [5,10] 上的维尔斯特拉斯定理,这意味着它在此区间的上下有界。
练习2
确定以下函数在建议的区间内是否具有最大值和/或最小值:
![]()
➤请参阅:有理函数的域
首先我们分析有理函数的连续性:
![]()
![]()
![]()
![]()
然而,该函数在 x=2 处呈现不连续性,这意味着它在区间 [-3,3] 上不连续。
简而言之,该函数不满足维尔斯特拉斯定理,因此我们不能说它在该区间内是否具有最小值或最大值。
练习3
确定以下函数在建议的区间内是否具有最大值和/或最小值并计算这些点:
![]()
➤参见:二次函数的特征
任何二次函数的定义域都是实数:
![]()
因此,该函数在区间 [0,4] 上连续并且满足 Weierstrass 定理。因此,该函数在此区间上具有绝对最小值和绝对最大值。
此外,该抛物线的顶点恰好位于 x=0 处,因此该函数在区间 [0,4] 上严格递增,因此最小值位于 x=0 处,最大值位于 x= 4 处。
![]()
![]()
卡尔·维尔斯特拉斯
一旦我们了解了维尔斯特拉斯定理的含义,我们将简要解释该定理的发明者是谁。
卡尔·西奥多·威廉·维尔斯特拉斯是19世纪德国一位非常重要的数学家,更准确地说,他于1815年10月31日出生于奥斯坦费尔德,于1897年2月19日逝世于柏林。
除了维尔斯特拉斯定理外,他还因其对数学的其他贡献而闻名。其中,他给出了函数的三个非常重要的概念连续性、极限和导数的定义。
同样,他成功地证明了当时尚未在数学上验证的某些定理,例如博尔扎诺-韦尔斯特拉斯定理、中值定理或海涅-博雷尔定理。
令人好奇的是,有一个月球陨石坑和一颗小行星以维尔斯特拉斯的名字命名,以纪念他。