欧拉公式是一个数学概念,它将两个基本数学概念联系起来:复数和三角学。这使得它成为所有数学中最重要的概念和最广泛的应用之一。在整篇文章中,我们将看到这个公式的样子以及它的所有用途。
欧拉公式是什么?
欧拉公式是基于欧拉数的基本数学方程,它将复数与三角学联系起来。它由瑞士数学家莱昂哈德·欧拉 (Leonhard Euler)在 18 世纪发现,此后被应用于从物理学到计算机科学的各个领域。
欧拉公式写为 e ix = cos(x) + i sin(x) ,其中 e 是自然对数的底数,i 是虚数单位(定义为 -1 的平方根),x 是实数数字。该方程指定复数 e ix等于实数 cos(x) 与虚数 i 与实数 sin(x) 的乘积之和。

欧拉公式的重要性在于它允许复数用实数和三角函数来表达,使它们更容易操纵和计算。
欧拉公式的证明
欧拉公式的证明基于对指数函数使用泰勒级数以及对余弦和正弦使用三角恒等式。
首先,我们考虑指数函数的泰勒级数:

接下来,我们将上式中的 x 替换为 ix,其中 i 是虚数单位(-1 的平方根):
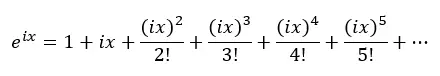
因此,我们应用 i 的幂并代入前面的方程:
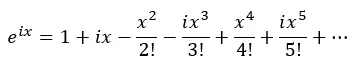
现在我们将实数项和带有 i 的项分组:
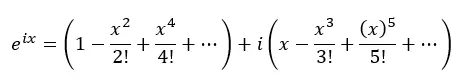
事实上,上面的每个括号都是余弦和正弦的泰勒级数:
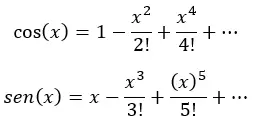
最后,我们简化(通过将括号中的每个表达式替换为 x 的余弦和正弦),我们得到:

欧拉公式示例
现在您已经了解了这个数学公式的工作原理,我们建议尝试解决以下实际示例:以二项式形式表示复数 e 2i (以弧度表示) :
欧拉公式的主要应用是将指数形式表示的复数转换为二项式形式。因此,我们将使用公式:e ix = cos(x) + i sin(x)
e 2i = cos(2) + i sin(2)
e2i = -0.416 + 0.909i
我们已经有了二项式形式的数字。从那里我们可以在复平面上进行图形表示。为此,有必要了解复数是在复平面中使用横坐标(x 轴)上的实部和纵坐标(y 轴)上的虚部作为坐标来表示的。
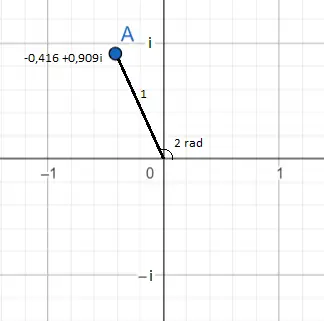
在上图中,显示了复数 e 2i ,它等于 -0.416 + 0.909i。这可以看作是一个蓝色的点。它在平面上的位置可以从两个角度看到。
第一个也是最明显的是以二项式形式表示的数字:-0.416(在横坐标上)和 0.909(在计算机上)。第二种是指数形式:e 2i的模等于1,因为它是e前面的数字(因为e前面没有数字,所以我们必须想象它有一个1)指数中有一个 2,因此,参数或角度相当于两个弧度。
如果您不太理解最后一段,我们建议您阅读我们有关复数的文章。好吧,我们对复数的不同写法及其所有属性进行了非常深入的解释。
欧拉公式的图形表示
在前面的示例中,您可以看到如何应用欧拉公式以及如何在复平面中以图形方式表示它。但是,如果我们更进一步并尝试表示一个与欧拉公式等效的函数,我们会发现一些非常奇怪的东西:它生成一个半径为 1 的圆:
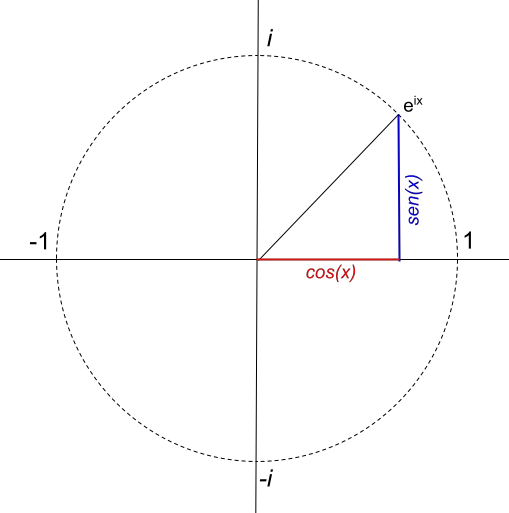
然而,圆的半径直接取决于复数的模的值。例如,如果我们要表示半径为 4 的圆,则函数将为 4e ix 。因此,函数 4e ix表示如下:
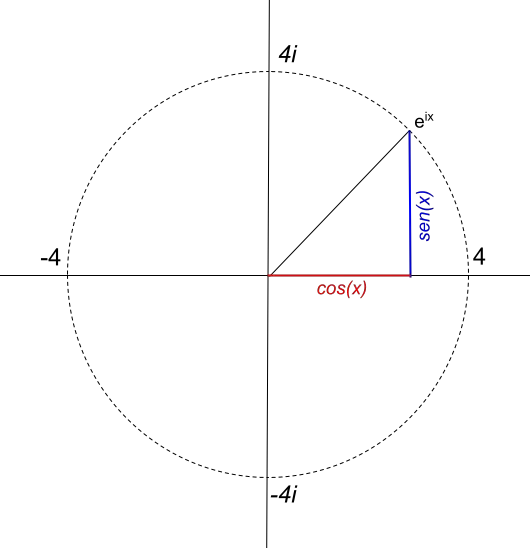
回到半径为1的圆,如果我们决定表示e iπ (以弧度为单位),我们必须首先计算:
e πi = cos(π) + i sin(π)
erπi = -1 + i 0
erπi = -1
我们得到 e πi = -1,这就是著名的欧拉恒等式。
由此我们推断,复数 e πi只有一个实部,等于-1。因此,其表示形式如下:
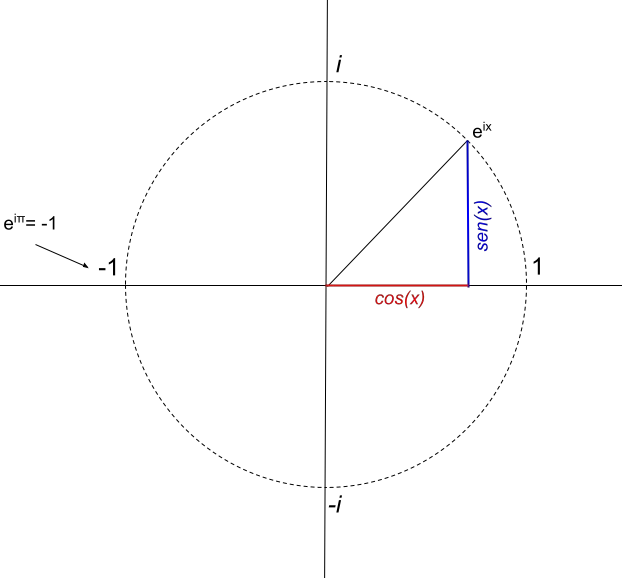
欧拉公式的应用
- 复数:欧拉公式是三角函数和复数之间的关系。根据这个公式,我们可以用不同的方式表达复数:二项式、指数式和极坐标。
- 泰勒级数:欧拉公式用于扩展泰勒级数函数。
- 线性代数:欧拉公式用于矩阵对角化,这是线性代数的基本技术。
- 微分和积分:欧拉公式用于微分方程的求解,这是微积分中的相关技术。
此外,它还应用于许多数学理论,甚至数学领域之外的概念,例如物理定理。
结论
正如您在本文中所看到的,欧拉公式的最大应用是在复数中:在其数值表达式和表示中。确实,这在代数中有一些应用,但本质上您正在处理复数。因此,首先要充分理解它们。
话虽这么说,我们希望我们已经帮助您更好地理解这个概念。如果您有任何疑问或不知道如何进行练习,请随时在评论中给我们写信。