在这里,您将找到有关平行线的所有内容:它们的含义、如何确定两条线是否平行、它们的属性等。此外,您将能够看到一些平行线的示例和已解决的练习。
什么是平行线?
平行线是那些永远不相交的线,也就是说,即使它们的轨迹延伸到无穷远,它们也永远不会互相接触。因此,两条平行线的点彼此之间的距离始终相同,而且两条平行线没有公共点。
例如,以下两条线是平行的:

我们一般用2个竖条||来表示两条线平行字里行间
另一方面,尽管两条平行线永远不会相交,但在解析几何中我们说它们形成 0° 角,因为它们具有相同的方向。
什么时候两条线平行?
一旦我们了解了平行线的定义,我们就会知道如何找到两条平行线。显然,一种方法是绘制线条并查看它们是否在图形上相交,但还有更简单且易于使用的方法。
确定两条线的平行度及其斜率
您可以通过查看每条线的斜率来判断两条线何时平行。请记住,直线的斜率是参数
![]()
由直线的显式方程和点斜率方程可得:
![]()
但是,确定直线斜率的方法有多种,因此要了解如何计算斜率,我们建议您查看直线斜率公式。此外,在链接页面上,您还可以找到有关直线斜率代表什么以及为什么它对直线如此重要的解释。
因此,在平面中,如果两条线具有相同的斜率(系数m)和在原点处的不同纵坐标(系数n),则两条线平行。
例如,以下两条线是平行的:
![]()
它们是两条平行线,因为它们都具有相同的斜率,而且它们的独立项不同。
![]()
![]()
应该注意的是,如果两条线具有相同的斜率并且同时位于原点的同一台计算机,则它们将是相同的线,因为它们将完全相同。
从隐式方程求两条直线的平行度
请记住,该直线的隐式(或一般)方程为:
![]()
因此,如果两条线的系数 A 和 B 彼此成比例,但与系数 C 不成比例,则意味着这两条线是平行的。
![]()
![]()
这是用一般(或隐式)方程形式表示的两条平行线:
![]()
它们是平行的,因为变量前面的数字
![]()
与变量前面的数字成正比
![]()
,但不具有独立项。
![]()
和之前一样,如果两条隐式线的所有系数(A、B 和 C)成比例,则意味着两条线重合,或者换句话说,它们相等。
平行线的性质
平行线的特点如下:
- 对称性:如果一条线与另一条线平行,则该线也与第一条线平行。垂直线也具有这个性质。
![]()
- 传递性:如果一条线与另一条线平行,并且第二条线与第三条线平行,则第一条线也与第三条线平行。
![Rendered by QuickLaTeX.com \left. \begin{array}{c} r \parallel s\\[2ex] s \parallel q \end{array} \right\} \longrightarrow \ r \parallel q](https://mathority.org/wp-content/ql-cache/quicklatex.com-d8ed30d043440defc6ebfd30c740e937_l3.png)
- 两条平行线的方向向量(表示线的方向的向量)的标量积等于它们的模的乘积。
![]()
- 此外,两条平行线的方向矢量始终彼此线性相关,因为它们成比例。
这个条件是直线平行的必要条件,但不是充分条件,或者换句话说,两条平行线必须具有成比例的方向向量,但两条直线具有成比例的方向向量这一事实并不直接意味着它们是平行的。由于重合线也具有成比例的方向矢量。
- 平行于横坐标轴(X 轴)的线是水平的,并且始终具有以下形式

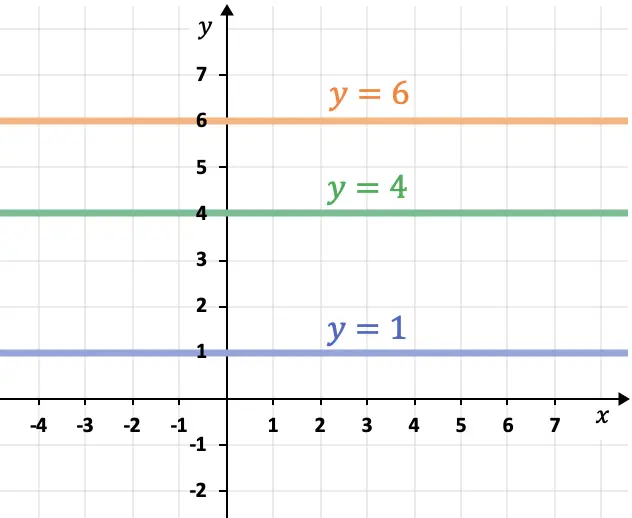
- 平行于计算机轴(Y 轴)的线是垂直的,并且始终遵循表达式

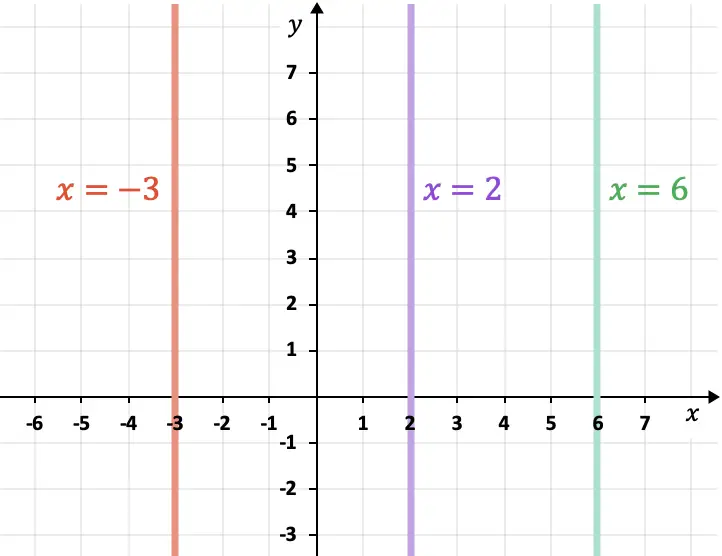
如何计算平面内两条平行线之间的距离
要找到平面中两条平行线之间的距离(在 R2 中),只需在两条线上取一点并计算从该点到另一条线的距离即可。
我们可以这样做,因为两条平行线之间的距离始终相同。

另一方面,如果使用公式时我们得到的距离为 0 个单位,则意味着这些线在某个点彼此接触,因此,这些线不是平行的,而是相交、重合或垂直的。如果您愿意,您可以在我们的网站上查看此类线路之间的差异。
因此,您可以看到这是如何完成的,我们将确定以下两条平行线之间的距离作为示例:
![]()
我们需要做的第一件事是在一条线上(您想要的线)上得到一个点。在这种情况下,我们将计算线上的一个点
![]()
为此,我们必须为其中一个变量赋予一个值,例如我们将这样做
![]()
![]()
现在我们清除另一个变量(
![]()
)得出的方程可以知道此时它的价值:
![]()
![]()
![]()
因此,从直线得到的点
![]()
东方:
![]()
一旦我们在一条线上有了一个点,我们就可以使用点到线距离的公式来计算从该点到另一条线的距离:
![]()
![]()
因此两条平行线之间的距离相当于 0.45 个单位。
平行线解决的问题
练习1
下面哪条线是平行的?
![Rendered by QuickLaTeX.com \begin{array}{l} r: \ y=2x+3 \\[2ex] s: \ y=3x-2 \\[2ex] q: \ y=2x+6 \\[2ex] t: \ y=-2x-4\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1baec7cae9d15180df86f9cf4f44d828_l3.png)
如果两条线具有相同的斜率(和不同的截距),则它们是平行的。因此,每条线的斜率是:
![]()
![]()
![]()
![]()
所以只有直线是平行的
![]()
和
![]()
因为它们是唯一具有相同坡度的。
练习2
求与直线平行的直线的显式方程
![]()
以及整个过程中会发生什么
![]()
说直话
![]()
![]()
使得线与线平行
![]()
两者必须具有相同的斜率。和线的斜率
![]()
是 3:
![]()
因此,我们需要找到的直线的显式方程为:
![]()
一旦我们知道了直线的斜率,我们就可以通过将属于直线的点代入直线方程来计算截距:
![]()
![]()
![]()
![]()
所以该直线的显式方程为:
![]()
练习3
计算未知数的值
![]()
和
![]()
使得以下两条线平行:
![]()
这些线以一般(或隐式)方程形式描述。因此,要使两条直线平行,它们的系数A和B必须成比例,即必须满足以下方程:
![]()
因此,我们必须求解前面的方程以获得未知值
![]()
为此,我们将分数交叉相乘:
![]()
![]()
![]()
另一方面,对于平行的线,它们的独立项不能与其他系数成比例:
![]()
因此,和以前一样,我们通过交叉相乘分数来求解不等式:
![]()
![]()
![]()
简而言之,让两条线平行
![]()
必须是 2 并且
![]()
可以是除 3 之外的任何实数。
练习4
下面两条平行线之间的距离是多少?
![]()
首先,我们将验证这是两条平行线。为此,变量的系数
![]()
和
![]()
必须彼此成比例,但不与独立项成比例:
![]()
事实上,这些线是平行的,因此我们可以应用该过程。
现在我们需要从其中一条线(您想要的线)中获取一个点。在这种情况下,我们将计算线上的一个点
![]()
为此,您必须为其中一个变量赋值,例如我们将这样做
![]()
![]()
现在我们清除另一个变量(
![]()
) 得到的方程即可知道此时的值:
![]()
![]()
![]()
这样从直线上得到的点
![]()
东方:
![]()
一旦我们知道一条线上的点,我们就可以使用以下公式计算从该点到另一条线的距离:
![]()
![]()