平行平面

在此页面上，您将找到有关平行平面的所有内容：当两个平面平行时、两个平行平面的方程、示例、已解决的练习、属性……

什么是两个平行平面？

在解析几何中，当两个平面始终相距相同的距离时，它们是平行的。因此，两个平行平面永远不会相交，也没有任何共同点。

平行放置的两个平面并不是平面之间唯一可能的相对位置，因为空间中的两个平面（在 R3 中）也可以相交或重合。

如何知道两个平面是否平行？

了解了平行平面的定义后，让我们看看如何确定两个平面是否平行。

从两个不同计划的一般（或隐式）方程开始：

如果两个平面的系数 A、B 和 C 彼此成比例且与系数 D 不成比例，则这两个平面将平行。换句话说，当满足以下等式时，两个平面之间就会平行：

两个平行平面的示例

例如，以下两个平面是平行的：

这些计划是并行的，因为变量 X、Y、Z 的系数彼此成比例，但与独立项不成比例：

计算两个平行平面之间的距离

两个平行平面的距离总是相同，因此，要找到两个平行平面之间的距离，我们可以在两个平面之一上取一点，然后计算从该点到另一个平面的距离。因此，要计算两个平行平面之间的距离，必须知道一点到平面的距离公式。

它是一种求两个平行平面之间距离的方法。然而，当两个平面方程的系数 A、B 和 C 重合时，还有一种更简单的方法：

考虑两个平行平面的一般（或隐式）方程：

两个平行平面之间距离的计算公式为：

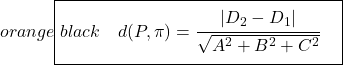
因此，使用公式肯定更容易找到两个平行平面之间的距离，因为这只是应用公式的问题，仅此而已，但这取决于问题。此外，我们认为最好解释两种计算距离的方法，以便您可以选择您喜欢的一种。

计算两个平行平面之间的距离的示例

作为示例，我们将计算以下两个平面之间的距离：

我们必须首先验证我们正在处理两个平行平面。因此，除了独立项之外，平面方程的所有系数都是成比例的，因此它们实际上是两个平行平面。

在这种情况下，两个平面方程的 A、B 和 C 项并不重合，但我们可以通过将第二个平面的整个方程除以 2 来实现这一点：

因此，两个平面的方程现在具有相同的系数 A、B 和 C。因此，我们可以使用两个平行平面之间的距离公式轻松计算两个平面之间的距离：

我们代入数值并求解运算：

使得一个平面和另一个平面之间的距离等于一。

平行平面的性质

平行平面的特点如下：

• 自反性：每个平面都与其自身平行。

• 对称性：如果一个平面与另一个平面平行，则该平面也与第一个平面平行。垂直平面也具有这个性质。

• 传递性：如果一个平面平行于另一个平面，并且该第二平面平行于第三平面，则第一平面也平行于第三平面。