在本文中,我们将解释什么是常数函数以及它的图形表示形式。此外,您将能够看到常量函数的几个示例以及此类函数的所有特征。最后,您将能够通过已解决的常数函数练习进行训练。
什么是常数函数?
常数函数是对于自变量 (x) 的任何值始终采用相同图像的函数,即常数函数的形式为f(x)=k ,其中 k 是任意实数。
![]()
常数函数的图形表示是一条水平线。
例如,以下所有函数都是常量:
![]()
常数函数的图形表示
一旦我们了解了常函数的概念,我们就会看到如何在图中表示常函数。
绘制常量函数的图形非常简单,只需在函数 (k) 的值中画一条水平线即可。
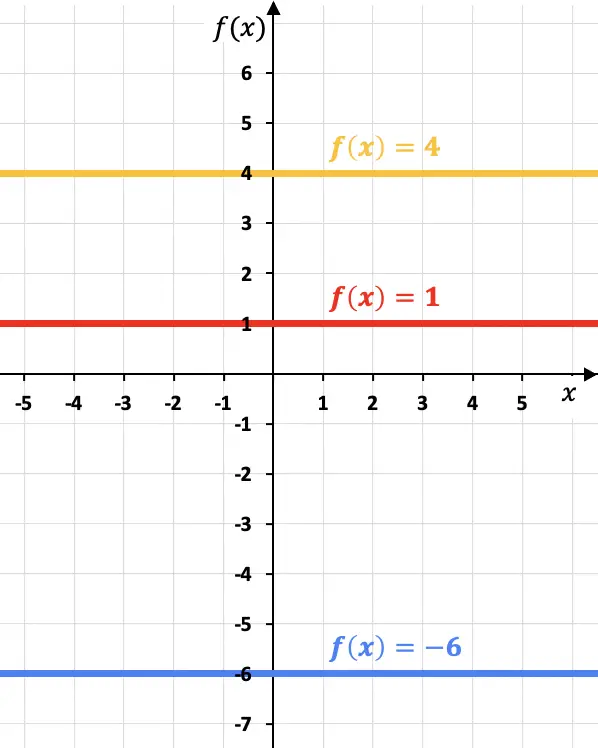
看下面的示例,其中我们在图上表示了三个不同的常量函数:

请注意,每个常数函数都平行于 x 轴。
另一方面,您必须记住垂直线不是常数函数。事实上,垂直线甚至不是函数,因为根据定义,函数对于每个 x 值只能有一个图像。
常数函数的特点
接下来我们来分析一下常函数的性质。考虑任意值的常量函数:
![]()
- 常数函数的定义域都是实数:
![]()
- 常数函数的路径或范围只是常数的值:
![]()
- 它是连续偶函数,因为该函数始终取相同的值:
![]()
- 常数函数既不增加也不减少,它是一种斜率始终为零的函数:
![]()
- 它始终与 OY 轴相交于点 (0,k)。
![]()
- 每个常数函数都是零次多项式。
- 是的
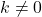
常数函数没有根,相反,如果
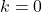
所有实数都是常数函数的根。
- 当 x 接近正无穷大或负无穷大时,常数函数的极限等于常数的值:
![]()
![]()
- 常数函数的导数始终为零:
![]()
事实上,常数函数的定义也可以从导数的概念来完成:如果一个函数的导数在其整个域上消失,则该函数是常数。
- 常数函数的积分是线性(或仿射)函数:
![]()
➤请参阅:什么是线性函数?
区间上的常数函数
我们已经看到函数如何保持恒定,但是,函数只能在其定义域的区间内保持恒定。
为了理解这个概念,您需要知道哪些函数是在块中定义的,因此在继续之前我们建议您看一下以下解释:
➤请参阅:什么是分段函数?
了解这些类型的函数是什么后,请查看下面所示部分中定义的函数:

从图中可以看出,该函数在其域内的所有数字中都不是恒定的。但它在区间[-2,4)内是常数,因此它仅在一个区间内是常数函数。
常量函数已解决的问题
练习1
确定下列哪些函数是常量:
![]()
第一个函数,
![]()
,是一个常量函数,因为无论变量 x 取什么值它总是 4。
第二个函数,
![]()
,不是常数函数,因为该函数的值根据 x 的值而变化。它是一个仿射函数。
第三个函数,
![]()
,对于任何 x 值都始终等于 0,因此它确实是一个常数函数。
第四个函数,
![]()
,不是常数函数,因为它根据 x 的值而变化。它是一个线性函数。
练习2
求通过点 (0.6) 的常数函数。
从代数角度来说,常数函数的公式始终具有相同的形式:
![]()
从图形上看,常数函数始终是一条水平线,因此,常数函数的坐标始终相等且有价值
![]()
由于函数经过的点的坐标 y=6,因此我们在这个问题中寻找的常数函数必须是:
![]()
练习3
在同一张图上绘制以下常量函数:
![]()
要表示每个常数函数,只需在每个常数的高度处画一条水平直线: