带参数方程组的讨论 -

在本页中，我们将了解如何讨论和求解带参数的方程组。此外，您还将找到线性方程组的示例和已解决的练习来进行练习。

另一方面，要分析线性方程组，了解什么是克莱默法则以及什么是鲁歇-弗罗贝尼乌斯定理非常重要，因为我们将不断使用它们。

带参数的线性方程组示例

根据参数m讨论并求解以下方程组：

$\begin{cases} x+y+2z= 2 \\[1.5ex] -x+my+2z=0 \\[1.5ex] 3x+mz = 4\end{cases}$

我们首先制作系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & m & 2 & 0 \\[1.1ex] 3 & 0 & m & 4 \end{array} \right)$

现在我们使用 Sarrus 规则求解 A 的行列式，看看矩阵的秩：

$\displaystyle\begin{aligned} \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} & =m^2+6+0-6m-0+m \\ & = m^2-5m+6 \end{aligned}$

因此 A 行列式的结果取决于m的值。因此，我们将看到行列式对于m的哪些值消失。为此，我们将结果设置为 0 ：

$\displaystyle m^2-5m+6 = 0$

我们用以下公式求解二次方程：

$\displaystyle m = \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle m = \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1 \cdot 6}}{2 \cdot 1} = \cfrac{5 \pm \sqrt{25-24}}{2} =\cfrac{5 \pm 1}{2} = \begin{cases} \bm{m = 3} \\[2ex] \bm{m =2} \end{cases}$

所以当m等于2或3时，A的行列式将是0。而当m不等于2且不等于3时，A的行列式将不等于0。

因此，我们必须针对每种情况分别进行分析：

m≠3 和 m≠2：

正如我们刚才看到的，当参数m不等于 2 和 3 时，矩阵 A 的行列式不等于 0。因此， A 的秩为 3 。

$\displaystyle rg(A)=3$

此外，矩阵 A’ 的秩也是 3 ，因为它内部有一个行列式不为 0 的 3×3 子矩阵。并且它的秩不能为 4 ，因为“我们无法创建 4×4 行列式”。

$\displaystyle rg(A')=3$

然后，由于矩阵 A 的秩等于矩阵 A’ 的秩和系统的未知数 (3)，根据Rouché-Frobenius 定理，我们知道它是确定兼容系统(SCD) :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

一旦我们知道系统是兼容确定系统（DCS），我们就应用克莱默规则来解决它。为此，请回想一下矩阵 A、其行列式和矩阵 A’ 为：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} = m^2-5m+6$

为了使用克莱默法则计算 x，我们将矩阵 A 的行列式的第一列更改为独立项的列，并将其除以 A 的行列式：

$\displaystyle\bm{x} = \cfrac{\begin{vmatrix} 2 & 1 & 2\\[1.1ex]0&m&2 \\[1.1ex] 4 & 0 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{2m^2+8-8m}{m^2-5m+6}$

为了使用克莱默法则计算 y，我们将 A 的行列式的第二列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 0 & 2 \\[1.1ex] 3 & 4 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-4+2m}{m^2-5m+6}$

为了用克莱默法则计算 z，我们将 A 的行列式的第三列改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-2m+4}{m^2-5m+6}$

因此，对于 m≠3 和 m≠2 的情况，方程组的解为：

$\displaystyle \bm{x =} \cfrac{\bm{2m^2+8-8m}}{\bm{m^2-5m+6}} \qquad \bm{y=} \cfrac{\bm{-4+2m}}{\bm{m^2-5m+6}} \qquad \bm{z =} \cfrac{\bm{-2m+4}}{\bm{m^2-5m+6}}$

正如您所看到的，在这种情况下，方程组的解是 m 的函数。

一旦我们找到了 m 不等于 2 和 3 时的解，我们就可以求解 m 等于 2 时的方程组：

米=2：

现在我们将分析参数m等于 2 时的系统。在这种情况下，矩阵 A 和 A’ 为：

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 2 & 2 \\[1.1ex] 3 & 0 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 2 & 2 & 0 \\[1.1ex] 3 & 0 & 2 & 4 \end{array} \right)$

正如我们之前看到的，当 m=2 时，A 的行列式为 0。因此，矩阵 A 的秩不是 3。但其内部有 2×2 个不同于 0 的行列式，例如：

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0$

因此，在这种情况下，A 的秩为 2 ：

$\displaystyle rg(A)=2$

一旦我们知道了矩阵 A 的秩，我们就可以计算 A’ 的秩。前 3 列的行列式给出 0，因此我们尝试矩阵 A’ 中其他可能的 3×3 行列式：

$\displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 0 & 2 & 4 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 2 & 4 \end{vmatrix}=0\qquad \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}=0$

维度 3×3 的所有可能的行列式都给出 0。但是，显然，矩阵 A’ 具有与矩阵 A 相同的 2×2 非 0 行列式：

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0$

因此，矩阵 A’ 的秩也是 2 ：

$\displaystyle rg(A')=2$

因此，由于矩阵 A 的秩等于矩阵 A’ 的秩，但这两个值均小于系统 (3) 的未知数个数，因此根据Rouché-Frobenius 定理可知，这是一个不定相容系统（工业控制系统）：

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

既然是ICS，就需要对系统进行改造来解决。为此，我们必须首先从系统中消除一个方程，在这种情况下，我们将删除最后一个方程：

$\begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \\[1.5ex] \cancel{3x+2z = 4} \end{cases} \longrightarrow \quad \begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0\end{cases}$

现在让我们将变量 z 转换为 λ：

$\begin{cases}x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+y+2\lambda= 2 \\[1.5ex] -x+2y+2\lambda=0\end{cases}$

我们将带有 λ 的项与独立项放在一起：

$\begin{cases}x+y=2-2\lambda \\[1.5ex] -x+2y=-2\lambda \end{cases}$

因此，系统的矩阵A和矩阵A’仍为：

$\displaystyle A= \left( \begin{array}{ccc} 1 & 1 \\[1.1ex] -1 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 1 & 2 -2\lambda \\[1.1ex] -1 & 2 & -2\lambda \end{array} \right)$

最后，一旦我们改变了系统，我们就应用克莱默规则。为此，我们首先求解 A 的行列式：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 \\[1.1ex] -1 & 2\end{vmatrix} =2-(-1)=3$

为了使用克莱默法则计算x ，我们将 A 的行列式的第一列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 -2\lambda & 1 \\[1.1ex] -2\lambda & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{4-4\lambda-(-2\lambda)}{3} = \cfrac{\bm{4-2\lambda}}{\bm{3}}$

为了使用克莱默法则计算y ，我们将 A 的行列式的第二列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 2 -2\lambda \\[1.1ex] -1 & -2\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-2\lambda -(-2+2\lambda)}{3} = \cfrac{\bm{2-4\lambda} }{\bm{3}}$

因此，当 m=2 时，方程组的解是 λ 的函数，因为它是 SCI，因此它有无限解：

$\displaystyle \bm{x =} \cfrac{\bm{4-2\lambda}}{\bm{3}} \qquad \bm{y=}\cfrac{\bm{2-4\lambda}}{\bm{3}} \qquad \bm{z=\lambda}$

我们已经分析了当参数m不等于 2 和 3 以及等于 2 时系统的解。因此我们只需要最后一种情况：当m取值 3 时：

米=3：

现在我们将分析当参数m为 3 时会发生什么。在这种情况下，矩阵 A 和 A’ 为：

$\displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 3 & 2 \\[1.1ex] 3 & 0 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 3 & 2 & 0 \\[1.1ex] 3 & 0 & 3 & 4 \end{array} \right)$

正如我们之前看到的，当 m=3 时，A 的行列式为 0。因此矩阵 A 不是 3 阶的。但它内部有 2×2 个不同于 0 的行列式，例如：

$\displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 3 \end{vmatrix} = 3 - (-1)=4 \neq 0$

因此，在这种情况下，A 的秩为 2 ：

$\displaystyle rg(A)=2$

一旦我们知道了矩阵 A 的秩，我们就可以计算 A’ 的秩。前 3 列的行列式给出 0，因此我们尝试矩阵 A’ 内的另一个 3×3 行列式，例如最后 3 列的行列式：

$\displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 3 & 2 & 0 \\[1.1ex] 0 & 3 & 4\end{vmatrix}=2$

另一方面，矩阵 A’ 确实包含一个结果不为 0 的行列式，因此矩阵 A’ 的秩为 3 ：

$\displaystyle rg(A')=3$

因此，当m=3时，矩阵A的秩低于矩阵A’的秩。因此，根据 Rouché-Frobenius 定理，我们推断出该系统是一个不相容系统（IS）：

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas}=3\end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A)=2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

因此，当 m = 3 时，方程组无解。

示例摘要：

正如我们所看到的，方程组的解取决于参数m的值。以下是所有可能情况的摘要：

m≠3 和 m≠2：

$\displaystyle \bm{SCD} \longrightarrow \begin{cases} x = \cfrac{2m^2+8-8m}{m^2-5m+6} \\[3.5ex] y =\cfrac{-4+2m}{m^2-5m+6} \\[3.5ex] z = \cfrac{-2m+4}{m^2-5m+6} \end{cases}$

米=2：

$\displaystyle \bm{SCI} \longrightarrow \begin{cases} x = \cfrac{4-2\lambda}{3} \\[3.5ex] y= \cfrac{2-4\lambda}{3} \\[3.5ex] z = \lambda \end{cases}$

米=3：

$\displaystyle \bm{SI} \longrightarrow$

系统无解。

这里我们使用鲁什定理和克拉默规则完成了整个过程，但是带参数的方程组也可以通过高斯方法（附练习）讨论和求解。您可以在链接页面上了解有关此方法的更多信息，您可以在其中找到该过程的详细说明以及示例和逐步解决的练习。

已解决的带参数线性方程组讨论问题

练习1

讨论并求解以下参数相关线性方程组：

查看解决方案

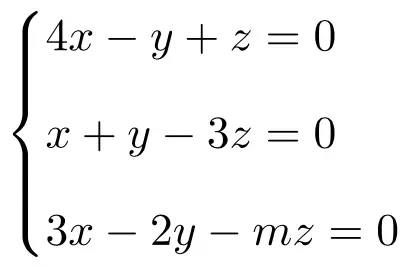
我们首先制作系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)$

我们现在必须找到矩阵 A 的秩。为此，我们检查整个矩阵的行列式是否不为 0：

$\displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{vmatrix} & =-4m+9-2-3-24-m \\ & =-5m-20 \end{aligned}$

A 行列式的结果取决于 m 的值。因此，我们将看到行列式对于 m 的哪些值消失。为此，我们将结果等于 0 并求解方程：

$-5m-20 = 0$

$-5m = 20$

$m = \cfrac{20}{-5} = -4$

所以，当m为-4时，A的行列式将为0。而当m不等于-4时，A的行列式将不同于0。因此，我们必须分别分析每种情况：

m≠-4：

正如我们刚才看到的，当参数m不等于-4时，矩阵A的行列式不等于0。因此，A的秩为3。

$\displaystyle rg(A)=3$

此外，矩阵 A’ 的秩也是 3，因为它内部有一个 3×3 子矩阵，其行列式不为 0。而且它的秩不可能是 4，因为“我们无法创建 4×4 行列式”。

$\displaystyle rg(A')=3$

因此，通过应用Rouché-Frobenius定理，我们知道这是一个兼容的确定系统（SCD），因为A的范围等于A’的范围和未知数的数量。

一旦我们知道系统是一个 SCD，我们就应用克莱默规则来解决它。为此，请回想一下矩阵 A、其行列式和矩阵 A’ 为：

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)$

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m\end{vmatrix} =-5m-20$

要使用克莱默规则计算 xatex]，我们将 A 行列式的第一列更改为独立项列，并将其除以 A 行列式：

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 0 & -1 & 1 \\[1.1ex] 0 & 1 & -3 \\[1.1ex] 0 & -2 & -m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

为了计算未知数并根据克莱默法则，我们将 A 行列式的第二列更改为独立项列，然后将其除以 A 行列式：

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & 0 & 1 \\[1.1ex] 1 & 0 & -3 \\[1.1ex] 3 & 0 & -m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

为了用克莱默法则计算 z，我们将 A 的行列式的第三列改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}$

因此，m≠-4情况下方程组的解为：

x=0 y=0 z=0

米=-4：

现在我们将分析参数 m 为 -4 时的系统。在这种情况下，矩阵 A 和 A’ 是：

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & 4 & 0\end{array} \right)$

正如我们之前看到的，当 m=-4 时，A 的行列式为 0。因此，矩阵 A 不是 3 阶的。但它内部有 2×2 个不同于 0 的行列式，例如：

$\displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0$

由于该矩阵具有不同于 0 的 2 阶行列式，因此矩阵 A 的秩为 2：

$\displaystyle rg(A)=2$

一旦我们知道了 A 的等级，我们就可以计算 A’ 的等级。我们已经知道前 3 列的行列式给出 0，因此我们尝试其他可能的 3×3 行列式：

$\displaystyle \begin{vmatrix} -1 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] -2 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] 3 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0\end{vmatrix} = 0$

矩阵 A’ 的所有 3×3 行列式均为 0，因此矩阵 A’ 也不会是 3 阶的。然而，它内部确实有不同于 0 的 2 阶行列式。例如：

$\displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0$

因此矩阵 A’ 的秩为 2：

$\displaystyle rg(A')=2$

矩阵 A 的范围等于矩阵 A’ 的范围，但这两者均小于系统 (3) 中的未知数数量，因此，根据 Rouché-Frobenius 定理，c 是不定相容系统 (ICS)：

这是一个ICS系统，所以我们需要对系统进行改造来解决它。我们首先消除一个方程，在本例中这将是最后一个方程：

$\begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0 \\[1.5ex] \cancel{3x-2y+4z = 0} \end{cases} \longrightarrow \quad \begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0\end{cases}$

现在让我们将变量 z 转换为 λ：

$\begin{cases}4x-y+z= 0 \\[1.5ex] x+y-3z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 4x-y+\lambda= 0 \\[1.5ex] x+y-3\lambda=0\end{cases}$

我们将带有 λ 的项与独立项放在一起：

$\begin{cases} 4x-y=-\lambda \\[1.5ex] x+y=3\lambda \end{cases}$

使得系统的矩阵A和矩阵A’保持：

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 \\[1.1ex] 1 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 4 & -1 & -\lambda \\[1.1ex] 1 & 1 & 3\lambda \end{array} \right)$

最后，一旦我们改变了系统，我们就应用克莱默规则。为此，我们首先求解 A 的行列式：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} = 4-(-1)=5$

为了使用克莱默法则计算 x，我们将 A 的行列式的第一列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix}-\lambda & -1 \\[1.1ex] 3\lambda & 1 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-\lambda-(-3\lambda)}{5} =\cfrac{\bm{2\lambda}}{\bm{5}}$

为了计算未知数并根据克莱默法则，我们将 A 行列式的第二列更改为独立项列，然后将其除以 A 行列式：

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & -\lambda \\[1.1ex] 1 & 3\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12\lambda-(-\lambda)}{5}=\cfrac{\bm{13\lambda}}{\bm{5}}$

因此，当 m=-4 时，方程组的解是 λ 的函数，因为它是 SCI，因此具有无限解：

$\displaystyle \bm{x =}\cfrac{\bm{2\lambda}}{\bm{5}}\qquad \bm{y=}\cfrac{\bm{13\lambda}}{\bm{5}} \qquad \bm{z=\lambda}$

练习2

讨论并求出以下参数相关线性方程组的解：

查看解决方案

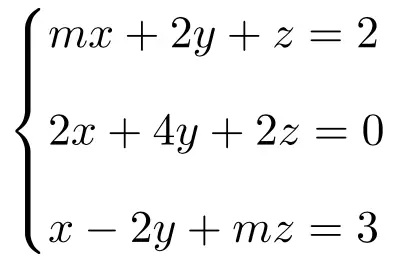
首先要做的是系统的矩阵A和扩展矩阵A’：

$\displaystyle A= \left( \begin{array}{ccc} m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}m & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & m & 3\end{array} \right)$

我们现在必须找到矩阵 A 的秩。为此，我们检查整个矩阵的行列式是否不为 0：

$\displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix} & =4m^2+4-4-4+4m-4m \\ & =4m^2-4 \end{aligned}$

A 行列式的结果取决于 m 的值。因此，我们将看到行列式对于 m 的哪些值消失。为此，我们将结果等于 0 并求解方程：

$4m^2-4 = 0$

$4m^2=4$

$m^2 = \cfrac{4}{4}$

$m^2 = 1$

$m = \pm 1$

因此，当m为+1或-1时，A的行列式将为0。而当m不同于+1和-1时，A的行列式将不同于0。因此，我们必须通过以下方式分析每种情况：

m≠+1 且 m≠-1：

正如我们刚才看到的，当参数m不等于+1和-1时，矩阵A的行列式不等于0。因此，A的秩为3。

$\displaystyle rg(A)=3$

此外，矩阵 A’ 的秩也是 3，因为它内部有一个 3×3 子矩阵，其行列式不为 0。而且它的秩不可能是 4，因为“我们无法创建 4×4 行列式”。

$\displaystyle rg(A')=3$

因此，通过应用Rouché-Frobenius定理，我们知道这是一个兼容的确定系统（SCD），因为A的范围等于A’的范围和未知数的数量。

一旦我们知道系统是一个 SCD，我们就应用克莱默规则来解决它。为此，请回想一下矩阵 A、其行列式和矩阵 A’ 为：

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix}=4m^2-4$

为了使用克莱默法则计算 x，我们将 A 的行列式的第一列更改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2& 2 & 1 \\[1.1ex] 0 & 4 & 2 \\[1.1ex] 3 & -2 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{8m+8}}{\bm{4m^2-4}}$

为了计算未知数并根据克莱默法则，我们将 A 行列式的第二列更改为独立项列，然后将其除以 A 行列式：

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} m & 2 & 1 \\[1.1ex] 2 & 0 & 2 \\[1.1ex] 1 & 3 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{-10m+10}}{\bm{4m^2-4}}$

为了用克莱默法则计算 z，我们将 A 的行列式的第三列改为独立项列，并将其除以 A 的行列式：

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix}m & 2 & 2 \\[1.1ex] 2 & 4 & 0 \\[1.1ex] 1 & -2 & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{12m-28}}{\bm{4m^2-4}}$

因此，对于 m≠+1 和 m≠-1 的情况，方程组的解为：

$\displaystyle \bm{x = }\cfrac{\bm{8m+8}}{\bm{4m^2-4}} \qquad \bm{y=}\cfrac{\bm{-10m+10}}{\bm{4m^2-4}}\qquad \bm{z =} \cfrac{\bm{12m-28}}{\bm{4m^2-4}}$

米=+1：

现在我们将分析参数 m 等于 1 时的系统。在这种情况下，矩阵 A 和 A’ 为：

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & 1 & 3\end{array} \right)$

正如我们之前看到的，当 m=+1 时，A 的行列式为 0。因此矩阵 A 不是 3 阶的。但它内部有 2×2 个不同于 0 的行列式，例如：

$\displaystyle \begin{vmatrix}2 & 4\\[1.1ex] 1 & -2 \end{vmatrix} =-4-4=-8 \neq 0$

由于该矩阵具有不同于 0 的 2 阶行列式，因此矩阵 A 的秩为 2：

$\displaystyle rg(A)=2$

一旦我们知道了 A 的等级，我们就可以计算 A’ 的等级。我们已经知道前 3 列的行列式给出 0，所以现在我们尝试使用最后 3 列的行列式：

$\displaystyle \begin{vmatrix} 2 & 1 & 2 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -2 & 1 & 3 \end{vmatrix} = 16$

另一方面，矩阵 A’ 确实包含一个 3×3 行列式，其结果不为 0，因此矩阵 A’ 的秩为 3：

$\displaystyle rg(A')=3$

因此，当m=+1时，矩阵A的秩小于矩阵A’的秩。因此，根据 Rouché-Frobenius 定理，我们推断出该系统是一个不相容系统（IS）：

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

因此，当 m=+1 时，方程组无解，因为它是一个不相容系统。

米=-1：

现在我们将分析参数 m 为 -1 时的系统。在这种情况下，矩阵 A 和 A’ 是：

$\displaystyle A= \left( \begin{array}{ccc} -1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}-1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & -1 & 3\end{array} \right)$

正如我们之前看到的，当 m=-1 时，A 的行列式为 0。因此，矩阵 A 不是 3 阶的。但它内部有 2×2 个不同于 0 的行列式，例如：

$\displaystyle \begin{vmatrix}-1 & 2\\[1.1ex] 2 & 4 \end{vmatrix} =-4-4=-8 \neq 0$

由于该矩阵具有不同于 0 的 2 阶行列式，因此矩阵 A 的秩为 2：

$\displaystyle rg(A)=2$

一旦我们知道了 A 的等级，我们就可以计算 A’ 的等级。我们已经知道前 3 列的行列式给出 0，所以现在我们尝试使用第 1、3 和 4 列的行列式：

$\displaystyle \begin{vmatrix} -1 & 1 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 1 & -1 & 3\end{vmatrix} = -20$

另一方面，矩阵 A’ 确实包含一个 3×3 行列式，其结果不为 0，因此矩阵 A’ 的秩为 3：

$\displaystyle rg(A')=3$

因此，当m=-1时，矩阵A的秩低于矩阵A’的秩。因此，根据 Rouché-Frobenius 定理，我们推断出该系统是一个不相容系统（IS）：

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

因此，当 m=-1 时，方程组无解，因为它是不相容系统。

带参数的线性方程组示例

示例摘要：

已解决的带参数线性方程组讨论问题

练习1

练习2

发表评论 取消回复

发表评论取消回复