十进制数在数学世界中非常重要,但我们真的知道它们是什么以及它们如何工作吗?在这篇文章中,我们将向您解释一切。
什么是小数?
小数是非整数(不包含在整数集内),具有整数部分和小数部分。该小数部分写在逗号后面,允许表达小于单位的值。
十进制数是表示带分数的一种方式。事实上,分数的概念与小数的概念非常相似。我们可以在下面的示例中看到这一点: 7/2 等于 3.5 。它们保持数字等价,只是写法不同。
数字“3.5”是一个十进制数,读作“三点五”,它的整数部分是3,它的小数部分等于5。由于十进制数是用十进制表示的,所以我们可以这样分解这个数:
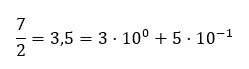
十进制命名法
在书写这些数字时,常用两种记数法:标准记数法(或十进制记数法)和科学记数法。第一个是最常见的,也是我们迄今为止使用过的。
科学记数法是标准记数法的缩写形式。在科学记数法中,十进制数被写为整数乘以10 的幂。例如,数量 0.0054 可以用科学记数法写为 5.4 · 10 -3 。
关于小数的非数字书写,我们使用一种表示法来表示每个小数位所占据的位置。嗯,就像整数部分有:个位、十位、百位……小数部分有:十分位、百位、千位……
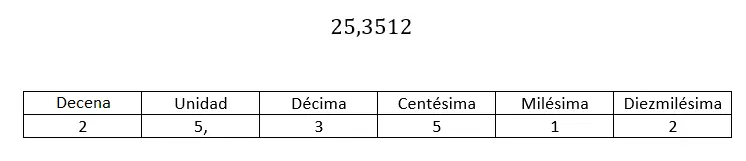
每个数字名称的标志是它相对于小数点所占据的位置。这样,当你有一个十进制数并且你想知道百分位的值是多少时,你必须查看第二位数字(从小数点向右)。在上述情况下,百分之一等于 5。
小数的类型
十进制数可以分类如下:
- 精确小数:具有确定且有限的小数位数。例如:9,263。
- 重复小数:小数点后位数无限。
- 纯循环小数:小数部分由无限重复的数字组成。例如:2.1515151515… 因为 15 无限重复。
- 混合重复小数:小数部分由一个值后面跟另一个无限重复的数字组成。例如:2.4615151515…由于46不重复。
- 不重复小数:小数部分无限大,不重复。在本节中,我们找到一些数学常数,即两个的平方根……

小数的性质
十进制数有几个属性,包括:
- 如果在右侧添加零,小数不会改变,因此数字 0.25 相当于 0.250 和 0.2500。基本上,因为它们表达的量相同。
- 小数相当于分数,例如半个单位(1/2)用0.5表示。
- 如果我们将十进制数乘以或除以 10 的幂,则必须将小数点移动:如果进行乘法则将小数点移至右侧,如果进行除法则将小数点移至左侧。
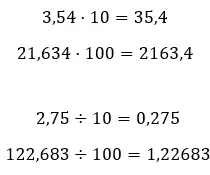
- 您可以简化小数,这是通过对小数进行四舍五入来完成的。此方法包括表示较少的十进制数字,并尽可能少地修改数字的值。如果您想了解如何使用此简化系统,我们建议您输入最后一个链接。
小数的表示
小数集可以像所有其他集合一样在数轴上表示。
从小数有整数部分和小数位(小于1)这一事实出发,我们可以推断出小数是在整数之间表示的。例如,数字0和1之间有无限位小数。您可以在下面看到它在行中的表示:
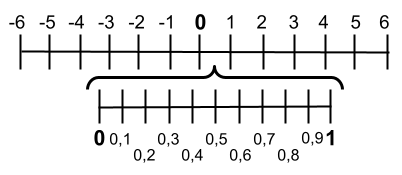
正如您在图中所看到的,我们已经写出了 0 和 1 之间的十分之一。尽管这两个数字之间有无限的小数位,但可以进行非常复杂的表示。更重要的是,这不仅发生在 0 和 1 之间,而且发生在所有整数之间。
小数的运算
小数的运算与整数的运算类似。唯一的区别是必须考虑小数位。因此,在求解运算之前,您必须确保始终使用相同的数字:十分之一与十分之一,百分之一与百分之一……
接下来,我们将简要回顾一下四种基本的小数算术运算:
- 小数相加:

- 小数减法:

- 小数乘法:

- 小数除法:

十进制数的用途和应用
小数在日常生活和数学中广泛使用。例如,当您在商店购买商品时,您需要知道所购买商品的价格,并且该价格将以十进制数字表示。此外,它们还用于测量距离、重量和日常生活的其他方面。
在数学中,十进制数使我们能够轻松地表达非常小或非常大的数量。它们还使我们能够进行更精确的计算。例如,如果我们要计算 3 个单位的一半,我们可以将其分成两等份,得到 1.5 个单位。