在此页面上,您将看到什么是对角矩阵以及对角矩阵的示例。此外,您还将了解如何使用此类矩阵、如何轻松计算其行列式以及如何对它们求逆。还有对角矩阵的性质和应用。最后,还有双对角矩阵和三对角矩阵的解释。
什么是对角矩阵?
对角矩阵是一个方阵,其中不在主对角线上的所有元素均为零 (0)。主对角线的元素可能为零,也可能不为零。
一旦我们知道对角矩阵的确切定义,我们将看到对角矩阵的示例:
对角矩阵的示例
维度为 2 × 2 的对角矩阵的示例
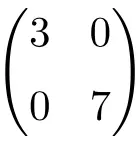
3×3 阶对角矩阵的示例

大小为 4×4 的对角矩阵的示例
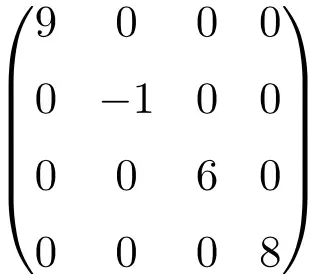
这些类型的矩阵通常表示对角线的元素:
![Rendered by QuickLaTeX.com diag(2,5,1) = \left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14216c3a6fd6e7bfd4c9d78ac2a4765c_l3.png)
对角矩阵的运算
对角矩阵对于线性代数如此重要的原因之一是它们可以让您轻松执行计算。这就是它们在数学中如此广泛使用的原因。
对角矩阵的加法和减法
两个对角矩阵相加(或相减)非常简单:只需将对角线上的数字相加(或相减)即可。
![]()
例如:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} +\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -4 \end{pmatrix} = \begin{pmatrix} 6& 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e659649fca7fe55f33c0f3452e8c46f2_l3.png)
对角矩阵乘法
要求解两个对角矩阵的乘法或矩阵乘积,只需将对角线的元素相乘即可。
![]()
例如:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & -4 & 0 \\[1.1ex] 0 & 0 & -3 \end{pmatrix} \cdot\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -18 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0bcb4a59778cc41eed67dce0bc384682_l3.png)
对角矩阵的幂
要计算对角矩阵的幂,我们需要对角矩阵的每个元素求指数:
![]()
![]()
例如:
![Rendered by QuickLaTeX.com \displaystyle\left. \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}\right.^3= \begin{pmatrix} 27 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 64 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d27337283f4b6029bff166fb8e3458d_l3.png)
对角矩阵的行列式
对角矩阵的行列式是主对角线上元素的乘积。
![]()
![]()
看一下下面已解决的练习,其中我们只需将其主对角线的元素相乘即可找到对角矩阵的行列式:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 5 \cdot 2 \cdot 3 = 30](https://mathority.org/wp-content/ql-cache/quicklatex.com-f34514c6e1559b8ebb296ee6c51a33d6_l3.png)
这个定理很容易证明:你只需要通过块(或辅因子)计算对角矩阵的行列式即可。下面使用通用对角矩阵详细介绍了该演示:
![Rendered by QuickLaTeX.com \begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & b & 0 \\[1.1ex] 0 & 0 & c \end{vmatrix}& = a \cdot \begin{vmatrix} b & 0 \\[1.1ex] 0 & c \end{vmatrix} - 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & c \end{vmatrix} + 0 \cdot \begin{vmatrix} 0 & b \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (b\cdot c) - 0 \cdot 0 + 0 \cdot 0 \\[2ex] & = a \cdot b \cdot c \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7b8718172b4b70d1ccacb01ea7ed5dd4_l3.png)
反转对角矩阵
当且仅当主对角线的所有元素都不为 0 时,对角矩阵才是可逆的。在这种情况下我们说对角矩阵是正则矩阵。
此外,对角矩阵的逆矩阵将始终是另一个具有主对角线的逆矩阵的对角矩阵:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \ \longrightarrow \ A^{-1}=\begin{pmatrix} \frac{1}{3} & 0 & 0 \\[1.1ex] 0 & \frac{1}{2} & 0 \\[1.1ex] 0 & 0 & \frac{1}{8} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a91beaaca82477a0c882b42da4eb7481_l3.png)
根据前面的特征,我们可以推导出对角矩阵的逆矩阵的行列式是主对角矩阵的逆矩阵的乘积:
![Rendered by QuickLaTeX.com \displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0571390802f955fac935aeb9cf4ab92f_l3.png)
![]()
对角矩阵的性质
- 任何对角矩阵也是对称矩阵。
- 对角矩阵是既是上三角又是下三角的矩阵。
- 单位矩阵是对角矩阵:
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e4e9931fb7ae104414006cee93978a7_l3.png)
- 同样,零矩阵也是对角矩阵,因为它不在对角线上的元素全部为零。虽然对角线上的数字都是0。
![Rendered by QuickLaTeX.com \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-edb061dcbc869eba51ece12af43f796f_l3.png)
- 对角矩阵的特征值(或特征值)是其主对角线的元素。
![Rendered by QuickLaTeX.com \begin{pmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} \longrightarrow \ \lambda = 3 \ ; \ \lambda = 4 \ ; \ \lambda = 7](https://mathority.org/wp-content/ql-cache/quicklatex.com-1dea3de2ae28d46194ead012bc001cf0_l3.png)
- 方阵是对角的当且仅当它是三角形且正规的。
- 对角矩阵的伴随是另一个对角矩阵。
对角矩阵应用
正如我们所看到的,用对角矩阵求解计算非常简单,因为运算中涉及许多零。因此,它们在数学领域非常有用并且被广泛使用。
出于同样的原因,人们对如何对矩阵进行对角化进行了很多研究,事实上,甚至已经开发了一种对角化矩阵的方法(使用特征多项式)。
因此,可对角化矩阵也非常相关。就像谱分解定理一样,它建立了矩阵何时可以对角化以及何时不能对角化的条件。
双对角矩阵
双对角矩阵是一种方阵,其中不在主对角线上或上下对角线上的所有元素均为 0。
例如:
![Rendered by QuickLaTeX.com \begin{pmatrix} 3 & 2 & 0 \\[1.1ex] 0 & -5 & 1 \\[1.1ex] 0 & 0 & 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d9acdfc09d0167548ef3f6f5b58d9276_l3.png)
上双对角矩阵
![Rendered by QuickLaTeX.com \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 0 & 7 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2b53f238add73431696006f4b05a2d8_l3.png)
下双对角矩阵
当主对角线和第一条上对角线都被占据时,我们称之为上双对角矩阵。另一方面,当主对角线和第一个次对角线都被占用时,我们称之为下双对角矩阵。
三对角矩阵
三对角矩阵是方阵,其唯一的非零元素是主对角线和上下相邻对角线的元素。
例如:
![Rendered by QuickLaTeX.com \begin{pmatrix} 2 & 3 & 0 & 0 \\[1.1ex] -4 & 5 & 9 & 0 \\[1.1ex] 0 & 1 & 6 & -2 \\[1.1ex] 0 & 0 & 8 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a8fbe0404c447268a89ff954e3b23d5_l3.png)
因此,所有对角、双对角和三对角矩阵都是带状矩阵的示例。因为带状矩阵是所有非零元素都位于主对角线周围的矩阵。