表示函数以便能够以图形方式分析构成该函数的不同变量之间的关系是很常见的。或者有时这些类型的表示甚至用于购买多种功能。这在进行统计研究时特别有用。话虽这么说,今天我们将向您解释一种非常简单的方法,只需 3 个步骤即可绘制任何函数的图形。此外,我们还将讨论如何分析图形结果以得出结论。
功能类型
首先,我们需要了解不同类型函数的特点以及表示它们时应考虑哪些差异。这样我们就可以更容易地进行图形表示,这就是为什么我们现在对每种类型进行简要评论。值得注意的是,函数的类型有很多种,因此我们将重点关注最重要的两种类型:多项式函数和分段函数。
线性函数
一次函数或一次多项式函数是其表达式为 1 次多项式的函数。则其表达式遵循模型f(x) = mx + n ,其中 m 为斜率,n 为纵坐标。基本上,这些函数具有相当于一条线的图形形式。您可以在下面看到一个示例:
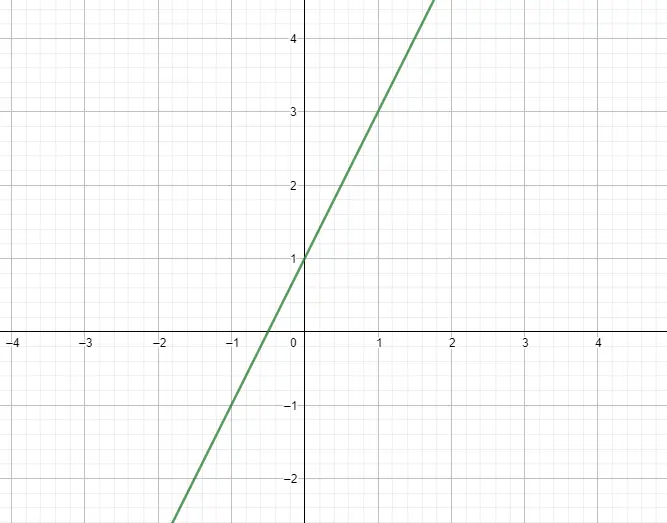
二次函数
二次函数或抛物线函数通过二次多项式表示,这就是它具有抛物线形式的原因。作为遵循的模型,我们将考虑以下表达式:f(x) = ax² + bx + c,其中 a ≠ 0。此外,这些函数还有两个值得注意的特征:幅度和增长。您可以在下面看到一个示例:
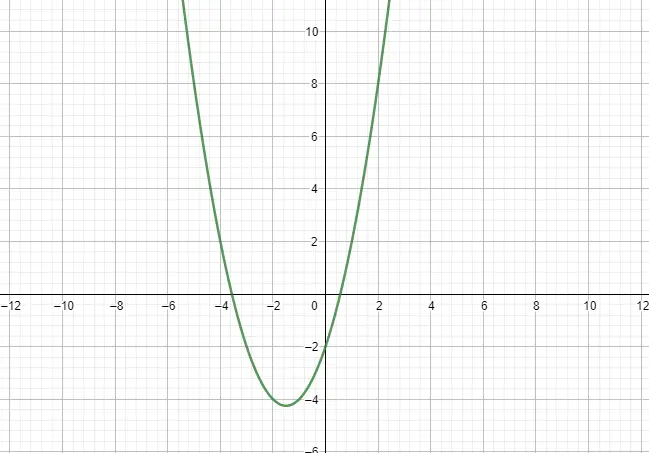
分段函数
分段定义的函数是根据 x 的值具有不同定义的函数。所以当x占据一定的取值范围时,我们需要尝试一个表达式。而当 x 占据其他值时,必须处理不同的表达式。正是在这里,我们发现了不连续性,因此也存在局限性。因为,当一个功能结束时,另一个功能可以开始,但无需直接连接。您可以在下面看到一个示例:
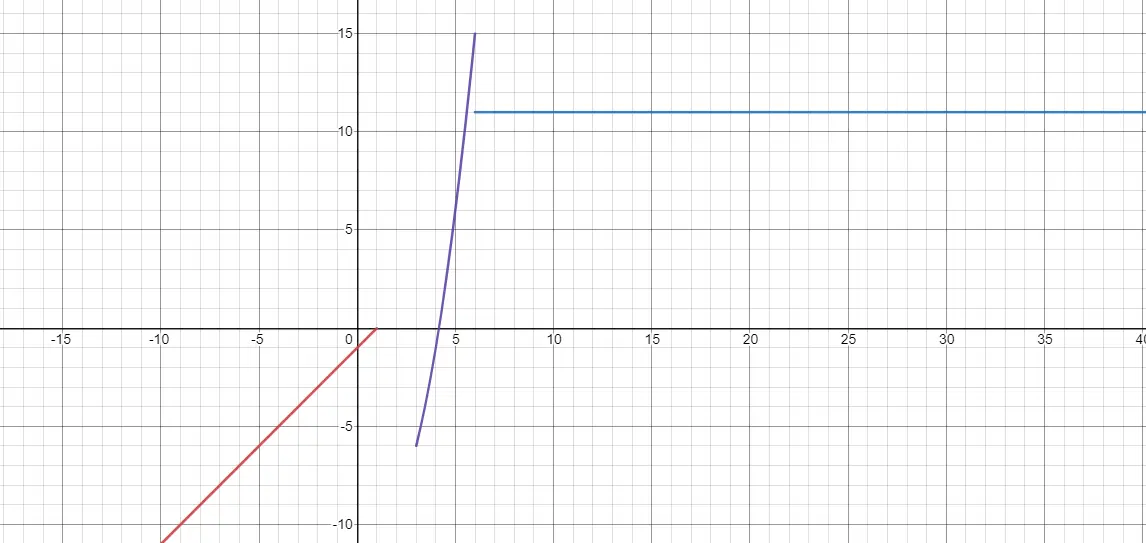
如何表示线性函数?
为了绘制线性函数的图形,我们需要遵循三个非常简单的步骤。接下来我们将解释该过程,但如果您想了解如何绘制抛物线函数的图形,我们建议您参阅下一节。
创建值表
为了能够绘制函数图表,我们需要创建一个值表,在其中写入变量的所有值。基本上,这将使我们能够在两个变量之间建立关系,这样我们就可以跟踪函数的路径。如果您不知道如何制作值表,可以查看最后一个链接。总之,它包括为自变量赋予一个值并将未知数代入与其相关的函数。这样我们就有了两个关联的数字,下表显示了一个示例:
根据函数 f(x) = 2x+1:
| X | f(x) |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
在图形上绘制点并通过绘制函数将它们连接起来
一旦我们制作了表格,我们就可以开始在图表上绘制点。我们通过将自变量与 x 轴相关联,另一个与 y 轴相关联来实现此目的,这样我们就可以获得点。您可以绘制任意数量的点,但要表示这种风格的函数,通常计算五个点就足够了。从那时起,他们就走上了一条笔直的道路,因此,无论你前进多远,它仍然是一样的。
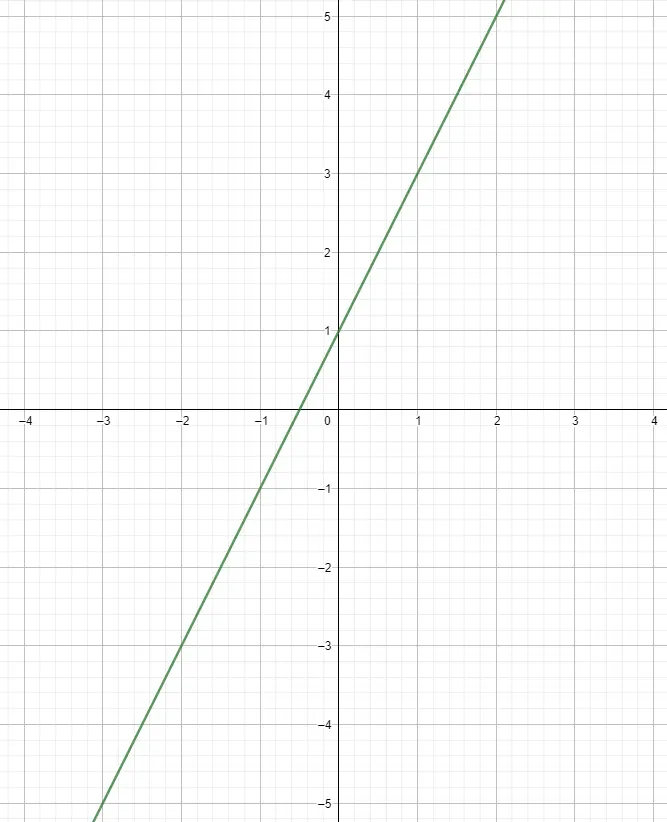
使用斜率绘制线性函数的图像
还有第二种方法可以在没有值表的情况下以图形方式表示线性函数,其中包括计算函数的斜率:m =(垂直变化/水平变化)。因此,一旦计算了斜率,我们就需要查看起点。回到前面的例子 f(x) = 2x+1,我们知道起点是 (0, 1),因为在 x = 0 时,计算机 = 1(我们从表达式中的 +1 推导出来) 。然后只需添加斜率,在本例中,斜率等于 1 水平方向的 +2 垂直方向。然后我们就会知道下一个点将是(1,3)。
如何表示二次函数?
为了表示二次函数,我们可以采用两种方法,第一种方法涉及值表。第二个包括计算一系列关键点:顶点、与 X 轴的交点以及与 Y 轴的交点。后者是我们将在下面解释的:
计算抛物线的顶点
有两个公式可以让我们计算抛物线函数的顶点,基本上一个给出了 X 轴的顶点,另一个给出了 Y 轴的顶点。您可以在下面找到这两个公式,但它们具有相似的结构。
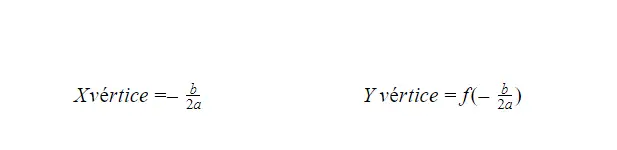
计算二次函数与 X 轴的交点
为了获得 的交点,我们所要做的就是求解方程,并且我们已经有了我们正在寻找的 X 值。值得注意的是,作为二次函数,我们将得到两个结果,而不仅仅是一个。
计算二次函数与 Y 轴的交点
最后,要获得与Y轴的交点,只需计算c = f(0)即可。由于当 x = 0 时,抛物线总是与垂直轴(纵坐标)相交,因此我们可以说 Y 轴的切割点为 (0,c)。一旦我们有了所有这些点,我们就可以将它们绘制在图表上,我们只需通过像这样绘制抛物线来将它们连接起来。
如何分段表示函数?
为了能够分段表示函数,您可以混合我们之前解释的所有方法。由于这种风格的函数是由我们讨论过的所有类型的函数组成的。因此,有些需要通过数值表来计算,而另一些则需要使用其他方法来计算。但是,一旦掌握了我们在本文中解释的内容,在分段表示函数时将不再遇到任何问题。
另一方面,由于在代表它们时您必须进行连续性研究,因此我们建议您学习如何解决限制(如果您还不知道如何解决)。这将帮助您正确表示每个函数的端点。话虽这么说,您现在已经准备好绘制分段函数和任何其他类型的函数的图形了。现在,我们为您提供一系列绘图技巧,并对计算器创建图表的功能进行非常有用的解释。
如何用计算器制作图表?
如果您有图形计算器,它将具有绘图功能。一旦您了解了该过程,这会很容易做到,但如果您仍然不知道如何操作,现在我们将向您解释。
- 访问图形模式:第一步是从菜单中访问图形或图形表示选项。此选项可能会为您的计算器标有不同的名称,但它将包含类似于图形或我们已经讨论过的单词。
- 自定义图形选项:进入图形编辑器后,我们必须为文件命名,标记轴,选择将绘制图形的元素数量并配置表示的美观选项。这是一个非常快速的步骤。
- 添加函数的点:然后您可以开始添加将形成图形的点。您可以通过使用以下符号书写点来完成此操作:(0,1)、(3,2)…并且您将继续添加点,直到完成绘图。
- 使用“预览”功能:完成项目后,您可以预览结果并查看结果是否符合预期。另外,许多模板都具有此预览的编辑选项,因此您可以调整结果直到完美。
- 保存项目:完成整个编辑过程后,请记住将其保存在易于记忆的位置。这样,无论何时您需要,您都可以再次访问该项目以进行查看或进行所需的改进。
表示函数的最佳计算器
如果您有兴趣购买能够在同一计算器上表示函数的图形模型,我们推荐两种型号: HP 50G和HP Prime 。这是两种最高质量的型号,尽管价格昂贵,所以您需要问自己这笔投资是否值得。例如,如果您要学习工程学等数学非常复杂的职业,那么强烈建议您购买这两种型号之一。但是,如果您不需要太多的计算或图形处理能力,也许Casio FX-9750GII就足够了。
如何在线绘制函数图?
您始终可以选择使用在线图形程序,例如: Desmos 、 Geogebra等。这样您就可以快速获得非常准确的图表。可以说,当您想要轻松快速地绘制函数图形时,可以使用数字形式。另一方面,如果您想要绘制函数图表,以便可以编辑它们(更改其所有属性)并轻松获得高质量的函数分析资源,那么我们建议您购买科学计算器。