在本页中,您将了解奇异矩阵或简并矩阵的含义。此外,我们还向您展示了几个示例,以便您没有疑问,最后,我们解释了此类矩阵的所有属性。
什么是奇异矩阵或简并矩阵?
奇异矩阵,也称为简并矩阵,定义如下:
奇异矩阵或简并矩阵是不可逆的方阵,因此其行列式等于0。
因此,要知道一个矩阵何时是奇异的,只需计算它的行列式:如果结果为0,则该矩阵是奇异的,反之,如果行列式不为0,则该矩阵不是奇异的。
如果您想了解更多有关逆矩阵的信息,可以参考此页面,其中详细解释了如何使用高斯方法求逆矩阵,您还会找到几个示例和逐步解决的练习来练习。
另一方面,奇异矩阵也称为非正则矩阵,因为它们的含义与正则矩阵正好相反。
奇异矩阵的示例
一旦我们了解了奇异矩阵或简并矩阵的解释,让我们看一些具有多个维度的奇异矩阵的示例:
2×2 奇异矩阵的示例
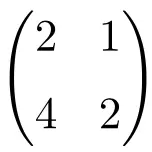
我们可以通过计算它的行列式很容易地验证它是一个奇异矩阵:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 2&1 \\[1.1ex] 4 & 2\end{vmatrix}\bm{=0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e8466c3a7108986306c5e06a6b49049_l3.png)
2阶矩阵的行列式等于0,因此是奇异矩阵。
3 × 3 奇异矩阵示例
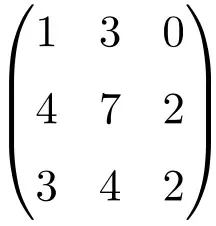
我们必须求解矩阵的行列式来验证它是一个不可逆矩阵:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 1&3&0\\[1.1ex] 4&7&2\\[1.1ex] 3&4&2\end{vmatrix}\bm{=0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1aebdc318be6773a6d4d78e9fcedaf5d_l3.png)
3 阶矩阵的行列式为 0,因此它是奇异矩阵。
4 × 4 奇异矩阵示例
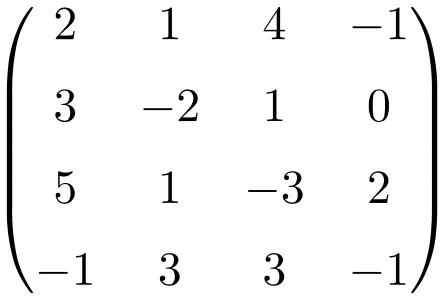
通过确定矩阵的行列式,我们可以证明它是奇异矩阵:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 2&1&4&-1\\[1.1ex] 3&-2&1&0\\[1.1ex] 5&1&-3&2\\[1.1ex] -1&3&3&-1\end{vmatrix}\bm{=0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ad6c7444321a65bb993c2abc87f93a0_l3.png)
4阶矩阵的行列式为零,因此其逆矩阵不存在。
警告:如果您对行列式的计算有疑问,可以查阅如何计算行列式页面。
奇异矩阵的性质
此类矩阵的特点如下:
- 奇异矩阵的至少两列或两行是线性组合并且是线性相关的。
- 任何包含用零填充的行或列的矩阵都是奇异矩阵。
- 奇异或简并矩阵的秩小于其大小。
- 奇异矩阵乘以任何其他矩阵的矩阵乘积给出另一个奇异矩阵。这个条件可以从行列式的性质推导出来:
![]()
- 同样,一个奇异矩阵的幂等于另一个奇异矩阵,无论它的幂是多少。
- 奇异矩阵的转置产生另一个奇异矩阵,因为转置(或转置)矩阵的行列式等价于非转置矩阵的行列式:
![]()
- 将奇异矩阵乘以标量不会改变其作为简并矩阵的状态。
- 奇异矩阵的伴随也是奇异的。
- 如果三角矩阵和对角矩阵的主对角线至少有一个元素为零,则它们是简并矩阵。
- 显然,零矩阵是奇异矩阵。
- 同理,幂零矩阵也是奇异矩阵。
- 与奇异矩阵相关的线性方程组无解或有无穷多个解。
- 最后,方阵是奇异的当且仅当它至少有一个特征值(或特征值)等于0。