如何计算多项式的根？（已解决的练习）

在此页面上，您将了解多项式的根是什么以及它们的计算方法。此外，您将能够看到逐步解决多项式根的示例和练习。

多项式的根是什么？

在数学中，多项式的根（或零点）是取消多项式的值。也就是说，多项式的根是在多项式中计算时数值等于 0 的所有值。

最终，

$x=a$

是多项式的根

$P(x)$

是的

$P(a)=0.$

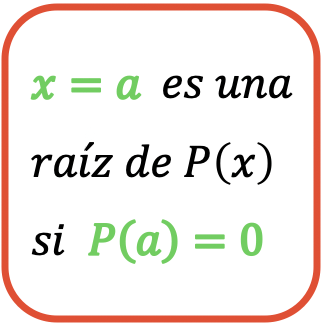
例如，如果我们有以下多项式：

$P(x)=x^2-3x+2$

我们可以验证多项式的根之一是 1，因为x=1处多项式的数值等于 0：

$P(1)=1^2-3\cdot 1+2 = 1-3+2 \color{blue} \bm{= 0}$

另一方面，3 不是多项式的根，因为它不是取消多项式的值，或者换句话说，多项式在x=3处的数值不同于零：

$P(3)=3^2-3\cdot 3+2 = 9-9+2=2 \color{blue} \bm{\neq 0}$

您现在可能更好地理解了多项式的根是什么，但是您不想知道多项式有多少个根吗？或者如何找到多项式的所有根？嗯，这正是我们将在下一节中看到的内容。

如何计算多项式的所有根？

要找到多项式的所有根，必须遵循以下步骤：

首先，计算多项式独立项的所有约数。
其次，在多项式中评估上一步中找到的所有值。
最后，如果当评估多项式中的一个数时其数值等于0，则该数是多项式的根。否则，所述数字不对应于多项式的根。

此过程是从余数定理推导出来的，单击此链接可了解此特定过程的原因。

计算多项式的根的示例

下面我们将一步步求解一个例子，以便您更好地理解如何求多项式的根。

以下多项式的所有根是什么？

$P(x) = x^2-5x+6$

首先，我们必须找到独立项的约数，因为多项式的每个根也是独立项的约数。所以，6的约数是：

6 的约数：+1、-1、+2、-2、+3、-3

请记住，如果一个数字是一个除数，那么它的负数也是一个除数。因为一个数可以被正数和负数整除。

因此，多项式的可能根或零点为：±1、±2、±3。因此，我们需要确定所有这些值的多项式的数值。为此，我们将这些值代入有 x 的多项式的表达式中：

$P(1) = 1^2 -5\cdot 1 +6= 1 -5 +6 =2$

$P(-1) = (-1)^2 -5\cdot (-1) +6 =1+5+6 = 12$

$P(2) = 2^2 -5\cdot 2 +6 =4-10+6= \color{blue} \bm{0}$

$P(-2) = (-2)^2 -5\cdot (-2) +6 =4+10+6 =20$

$P(3) = 3^2 -5\cdot 3 +6 =9-15+6=\color{blue} \bm{0}$

$P(-3) = (-3)^2 -5\cdot (-3) +6 =9+15+6 =30$

因此，只有当变量x为 +2 或 +3 时，多项式才会消失，所以这里是多项式的根：

多项式的根或零点：+2 和 +3

另一方面，请注意多项式的根与其次数一样多，也就是说，由于多项式是二阶，所以它有两个根。在多项式根的性质（如下）中，我们将看到为什么这个特征对于任何多项式总是成立。

我们刚刚看到了一种求多项式根的方法。然而，还有其他方法可以实现这一点，例如您还可以用鲁菲尼规则求多项式的根。单击以下链接查看鲁菲尼规则的示例，在这里您将发现这个众所周知的方法的组成部分，以及两个过程之间的区别。

多项式根的性质

多项式的根或零点具有以下特征：

正如我们之前所看到的，多项式的整数根（或零）是多项式独立项的约数。

如果我们知道多项式的所有根，我们可以将所述多项式表示为以下类型的二项式乘积的形式
$(x-a).$

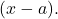
例如，多项式

$P(x) =x^3+3x^2-x-3$

它有 3 个根，分别是

$x=+1, x=-1$

和

$x=-3.$

因此，我们可以将多项式重写为 3 个因子乘法的形式，每个因子由变量形成

$x$

并且根已经改变了符号：

$\displaystyle\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60} P(x) =x^3+3x^2-x-3 \ \longrightarrow \ \text{ra\'ices} \begin{cases} x=\color{verd}\bm{+1} \\[2ex] x=\color{vermell}\bm{-1} \\[2ex] x=\color{blau}\bm{-3}\end{cases}$

$\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60}P(x) =x^3+3x^2-x-3 = (x\color{verd}\bm{-1}\color{black})\cdot (x\color{vermell}\bm{+1}\color{black}) \cdot (x\color{blau}\bm{+3}\color{black})$

这称为多项式因式分解。事实上，确定多项式根的主要应用之一是用于对其进行因式分解。在以下链接中，您可以了解这个非常特殊的运算的组成部分，此外，您还可以通过求解多项式因式分解练习进行练习。

多项式的根数与其次数相同。因此，二阶多项式有 2 个根，三阶多项式有 3 个根，四阶多项式有 4 个根，依此类推。

如果一个多项式没有独立项，则意味着它的一个根为0。那么其余的根一定是最低次单项式的系数的约数。

例如，以下多项式没有独立项：

$P(x) =x^3+x^2-2x$

因此多项式的一个根必然为0。其余的根是最低次项的系数的约数，即-2。更准确地说，其他根是

$x=+1$

和

$x=-2,$

所以多项式的所有根都是：

多项式的根或零点：0、+1 和 -2

当多项式的根无法确定时，称其为不可约多项式。

例如，我们将尝试计算以下多项式的根：

$P(x) =x^2+3x-1$

多项式唯一可能的根是 -1 的约数，即 -1 和 +1。因此，我们将多项式评估为这些值：

$P(1) = 1^2 +3\cdot 1 -1= 1 +3 -1 =3 \neq 0$

$P(-1) = (-1)^2 +3\cdot (-1)-1 =1-3-1 =-3 \neq 0$

在任何情况下，多项式都不会被取消，因此它没有根，因此它是一个不可约多项式。

当多项式是由几个多项式的乘积组成时，不需要做这个乘积来计算根，而是多项式的根是每个因子相乘的根。

例如，如果我们有以下多项式：

$P(x) = (x-2) \cdot (x+1)$

从多项式根的第二个性质，我们可以推断出左边多项式的根是+2，右边多项式的根是-1。

$\displaystyle (x-2) \ \longrightarrow \ \text{ra\'iz} \ x=+2$

$\displaystyle (x+1) \ \longrightarrow \ \text{ra\'iz} \ x=-1$

因此，由两个因子相乘得到的多项式的根是它们各自的根，即+2和-1。

$\displaystyle P(x) = (x-2) \cdot (x+1) \ \longrightarrow \ \text{ra\'ices} \ \begin{cases}x=+2 \\[2ex] x=-1 \end{cases}$

解决了多项式根的练习

练习1

确定是否

$x = -4$

是以下多项式的根：

$P(x)=x^3+2x^2-11x-12$

查看解决方案

找出是否

$x=-4$

是多项式的根，我们需要将其计算为该值。然而：

$\begin{aligned}P(-4)& =(-4)^3+2\cdot (-4)^2-11\cdot (-4) -12 \\[2ex] & = -64+2\cdot 16 +44 -12 \\[2ex] & = -64+32+44 -12 \\[2ex] & = 0 \end{aligned}$

多项式的数值

$x=-4$

为零，因此它实际上是多项式的根。

练习2

计算以下多项式的所有根：

$P(x)=x^2-3x+2$

查看解决方案

首先，为了找到多项式的可能根，我们必须找到独立项的约数。所以，2的约数是：

2 的约数：+1、-1、+2、-2

因此，多项式的可能根或零点为 ±1 和 ±2。因此，我们需要计算多项式在所有这些值中占多少：

$P(1)=1^2-3\cdot 1+2 =1-3+2=0$

$P(-1)=(-1)^2-3\cdot (-1)+2 =1+3+2=6$

$P(2)=2^2-3\cdot 2+2 =4-6+2=0$

$P(-2)=(-2)^2-3\cdot (-2)+2 =4+6+2=12$

因此，当x为 +1 或 +2 时，多项式消失，因此这里是多项式的根：

多项式的根或零点：+1 和 +2

练习3

求以下多项式的根：

$P(x)=x^3-x^2-4x+4$

查看解决方案

我们必须首先找到独立项的约数，因为多项式的根也是独立项的约数。所以，4 的约数是：

4 的约数：+1、-1、+2、-2、+4、-4

因此，多项式的可能根或零点为 ±1、±2 和 ±4。因此，我们必须在所有这些值中找到多项式的数值：

$P(1)=1^3-1^2-4\cdot 1+4 =1-1-4+4=0$

$P(-1)=(-1)^3-(-1)^2-4\cdot (-1)+4 =-1-1+4+4=6$

$P(2)=2^3-2^2-4\cdot 2+4 =8-4-8+4=0$

$P(-2)=(-2)^3-(-2)^2-4\cdot (-2)+4 =-8-4+8+4=0$

$P(3)=3^3-3^2-4\cdot 3+4 =27-9-12+4=10$

$P(-3)=(-3)^3-(-3)^2-4\cdot (-3)+4 =-27-9+12+4=20$

因此，多项式仅在x为 +1、+2 或 -2 时消失，因此这里是多项式的根：

多项式的根或零点：+1、+2 和 -2

练习4

求以下多项式的根：

$P(x)=x^3-6x^2+8x$

查看解决方案

在这种情况下，多项式没有独立项。因此，根据上面解释的根的第四个性质，我们知道多项式的根之一必须为0。

多项式的根：

$x=0$

此外，在这种情况下，可能的根不是独立项的约数，而是最低次项的系数的约数，即 8：

8 的约数：+1、-1、+2、-2、+4、-4、+8、-8

因此多项式的可能根或零点为 ±1、±2、±4 和 ±8。因此，我们必须计算所有这些值处的多项式的数值：

$P(1)=1^3-6\cdot 1^2+8\cdot 1 = 1-6+8=3$

$P(-1)=(-1)^3-6\cdot (-1)^2+8\cdot (-1) = -1-6-8=-15$

$P(2)=2^3-6\cdot 2^2+8\cdot 2 = 8-24+16=0$

$P(-2)=(-2)^3-6\cdot (-2)^2+8\cdot (-2) = -8-24-16=-48$

$P(4)=4^3-6\cdot 4^2+8\cdot 4 = 64-96+32=0$

$P(-4)=(-4)^3-6\cdot (-4)^2+8\cdot (-4) = -64-96-32=-192$

$P(8)=8^3-6\cdot 8^2+8\cdot 8 = 512-384+64=192$

$P(-8)=(-8)^3-6\cdot (-8)^2+8\cdot (-8) = -512-384-64=-960$

所以当x为+2或+4时多项式消失，所以这些值就是多项式的根。然而，我们还需要添加我们在问题开始时找到的根 0。总之，多项式的所有根为：

多项式的根或零点：0、+2 和 +4

练习5

利用多项式根的性质计算以下多项式的根：

$P(x)=(x-1)(x+3)(x^2-x-2)$

查看解决方案

正如我们在根的第六个性质中看到的，当多项式由因子乘积形成时，不需要计算所有的根，因为整个多项式的根就是每个因子的根。

此外，根据多项式根的第二个性质，我们可以推断出第一个因子的根是+1，第二个因子的根是-3。

$\displaystyle (x-1) \ \longrightarrow \ \text{ra\'iz} \ x=+1$

$\displaystyle (x+3) \ \longrightarrow \ \text{ra\'iz} \ x=-3$

所以我们只需要找到最后一个因子的根即可。为此，我们找到独立项 (-2) 的约数：

-2 的约数：+1、-1、+2、-2

所以最后一个多项式的可能根或零点是±1和±2。我们必须用它来计算所有这些值中所述多项式的数值：

$q(x)= x^2-x-2$

$q(1)=1^2-1-2=1-1-2=-2$

$q(-1)=(-1)^2-(-1)-2=1+1-2=0$

$q(2)=2^2-2-2=4-2-2=0$

$q(-2)=(-2)^2-(-2)-2=4+2-2=4$

因此，右边多项式的根是 -1 和 2。

因此，整个多项式的根就是所有找到的根：

多项式的根或零点：+1、-1、+2、-3

多项式的根是什么？

如何计算多项式的所有根？

计算多项式的根的示例

多项式根的性质

解决了多项式根的练习

练习1

练习2

练习3

练习4

练习5

发表评论 取消回复

发表评论取消回复