在此页面上,您将了解它是什么以及如何计算多项式的数值。此外,您将能够看到逐步解决多项式数值的示例和练习。
多项式的数值是多少?
在数学中,对于 x=a 的多项式 P(x) 的数值,即 P(a),是通过将多项式的变量 x 替换为数字 a 并执行所示计算而获得的结果在多项式表达式中。
为了让您更好地理解多项式数值的概念,下面我们通过一个例子来说明它是如何计算的:
如何计算多项式的数值
现在我们知道了多项式数值的数学定义,让我们通过一个例子来看看如何确定多项式的数值:
- 当 x=2 时,下列多项式的数值是多少?
![]()
为了求出多项式的数值,需要用问题给定的值来计算该多项式,也就是说,需要代入变量
![]()
多项式除以语句的值。因此,在这种情况下我们需要替换字母
![]()
对于 2:
![]()
一旦我们将值代入多项式的代数表达式中,我们就执行运算。所以我们首先求解幂:
![]()
现在我们计算乘法:
![]()
最后,我们添加和减去这些项:
![]()
总之,x=2 时多项式的数值等于 21。
正如您所看到的,求多项式的数值并不是很复杂,但它有一些非常有用的应用。例如,知道如何找到多项式的数值对于能够使用余式定理(关于多项式的一个非常重要的定理)至关重要。单击此链接,了解余数定理是什么,您将找到它的解释、使用示例和逐步解决的练习。
多项式数值示例
为了让您了解如何获取多项式的数值,我们为您提供了其他已解决的示例:
实施例1
- 计算多项式的数值
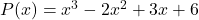
为了

![Rendered by QuickLaTeX.com \begin{aligned} P(-1) & =(-1)^3-2\cdot (-1)^2+3\cdot (-1)+6 \\[2ex] & = -1-2\cdot 1+3\cdot (-1)+6 \\[2ex] & =-1-2-3+6 \\[2ex]&= \bm{0} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3293713c5e12fac56d94be90f6bfc6e5_l3.png)
在这种情况下,多项式的数值等于 0。由于多项式的属性,这会产生影响,因为借助 因子定理,我们可以知道多项式之间某些除法的余数是什么。要了解更多信息,请单击上一个链接,我们在其中解释了这个定理是什么以及它的用途。
实施例2
- 确定多项式的数值
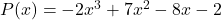
为了
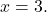
![Rendered by QuickLaTeX.com \begin{aligned} P(3) & =-2\cdot 3^3+7\cdot 3^2-8\cdot 3-2 \\[2ex] & =-2\cdot 27+7\cdot 9-8\cdot 3-2 \\[2ex] & =-54+63-24-2 \\[2ex]&= \bm{-17} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ad8b1145d569157b4e771adfae674e2c_l3.png)
到目前为止,我们只看到了如何以经典方式确定多项式的数值,但您应该知道还有另一种方法。更具体地说,您还可以使用Ruffini 方法计算多项式的数值。您还应该知道如何使用此过程,因此我们建议您在链接中查看其详细说明。
具有两个或多个变量的多项式的数值
我们刚刚了解了当多项式只有一个变量时如何求其数值。但是……当多项式有多个变量时,如何获得该多项式的数值呢?
那么,如果一个多项式有2个或更多的字母,那么它的数值必须以同样的方式计算,即先将多项式中的每个变量替换为其对应的值,然后求解多项式运算。
例如,您解决了以下此类问题:
- 求多元多项式的数值
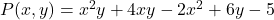
对于价值观
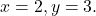
首先,我们将每个变量替换为其对应的值,即替换字母
![]()
对于 2,我们改变字母
![]()
通过 3:
![]()
我们求解权力:
![]()
现在我们计算乘积:
![]()
最后,我们进行加法和减法:
![]()
因此指令数据的多项式的数值相当于41。
已解决多项式数值练习
练习1
x=-2 时多项式 P(x) 的数值是多少?
![]()
要求多项式的数值,我们只需将语句中给出的值代入多项式表达式并求解结果运算即可:
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =-2\cdot (-2)^3-4\cdot (-2)^2+3\cdot (-2)+8 \\[2ex] & =-2\cdot (-8)-4\cdot 4+3\cdot (-2)+8 \\[2ex] & =+16-16-6+8 \\[2ex]&= \bm{2} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-93b7cf1a6c7e930a0a70fc8302f4012d_l3.png)
练习2
计算以下带分数多项式(x=4)的数值。
![]()
无论多项式是否有分数,求多项式数值的过程始终相同。因此,我们必须将变量 x 替换为 4 并求解计算:
![Rendered by QuickLaTeX.com \begin{aligned} P(4) & =\cfrac{1}{2} \cdot 4^2-\cfrac{5}{4}\cdot 4+ 7 \\[2ex] & =\cfrac{1}{2} \cdot 16-\cfrac{5}{4}\cdot 4+ 7\\[2ex] & =8-5+7 \\[2ex]&= \bm{10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04fa4389b5e7c5257937ad35aed07c7b_l3.png)
练习3
确定值 x=3、y=5 和 z=-2 的多项式的数值
![]()
要确定多元多项式的数值,只需将问题中给出的值代入代数表达式并求解所得运算即可:
![Rendered by QuickLaTeX.com \begin{aligned} P(3,5,-2) & =3^2\cdot 5\cdot (-2)+4\cdot 5^2\cdot (-2)^2-3\cdot 3^2\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =9\cdot 5\cdot (-2)+4\cdot 25\cdot 4-3\cdot 9\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =-90+400+54-180\\[2ex]&= \bm{184} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29683a91c14427a8ea42c3518e59e53f_l3.png)
练习4
给定多项式
![]()
计算参数值
![]()
以便
![]()
在这个问题中,求未知数的值
![]()
我们需要解方程
![]()
![]()
因此,我们首先尝试计算P(-2)的值:
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =-2\cdot (-2)^3-3\cdot (-2)^2+5\cdot (-2)+k \\[2ex] & =-2\cdot (-8)-3\cdot 4+5\cdot (-2)+k \\[2ex] & =+16-12-10+k\\[2ex]&=-6+k \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b58398099c8033b93a559e2f0c87f1a_l3.png)
现在我们将得到的表达式均衡为 5:
![]()
![]()
最后,我们求解所得方程:
![]()
![]()