在此页面上,您将找到有关如何完成多项式加法的说明。此外,您将能够看到多项式和的示例,甚至是逐步解决的练习。最后,我们还解释了此类多项式运算的性质。
如何添加多项式?
在数学中,要添加两个或多个多项式,必须将相似的多项式的项加在一起。也就是说,多项式相加就是将具有相同文字部分(相同变量和相同指数)的项相加。
因此,多项式的求和可以通过两种不同的方式完成:使用垂直方法或使用水平方法。以下是这两个过程的说明,但我们建议您先学习如何垂直添加多项式,然后再学习水平方法。显然坚持你喜欢的那个。
添加垂直多项式
接下来,我们将通过示例了解两个多项式如何垂直相加:
- 添加以下两个多项式:
![]()
![]()
我们需要做的第一件事是将一个多项式放在另一个多项式下面,以便两个多项式的相似项按列对齐:
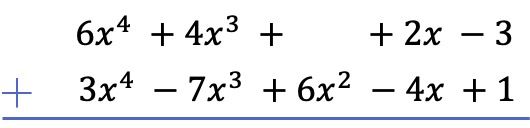
警告:如果多项式没有特定次数的项,则该空格必须留空。例如
![]()
您没有 2 次单项式,因此您的网站上有空白区域。
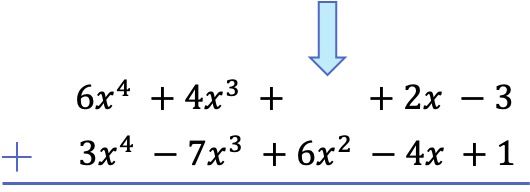
将所有项按从最高阶到最低阶的顺序排列后,我们将每列中的系数相加,保持文字部分相等:
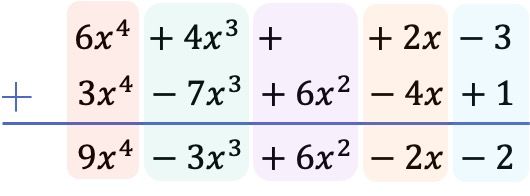
因此,两个多项式之和得到的结果是:
![]()
现在您已经了解了多项式的加法,并且知道您还可以对由多项式组成的分数进行加法。这种类型的运算称为代数分数加法。单击此链接,不仅可以了解如何计算代数分数之和,还可以了解如何求解所有代数分数运算。
多项式的水平加法
我们刚刚了解了如何垂直添加多项式,但现在我们将了解另一种添加多项式的方法:水平添加多项式。当然,这个过程比前一个过程要快,但是需要更好地掌握多项式的概念。
那么让我们通过一个例子来看看这种多项式相加的方法是由什么组成的。因此您可以看到两种方法之间的差异,我们将添加与上一个示例中相同的多项式:
- 计算以下两个多项式的和:
![]()
![]()
您必须首先将两个多项式置于同一运算中,也就是说一个接一个:
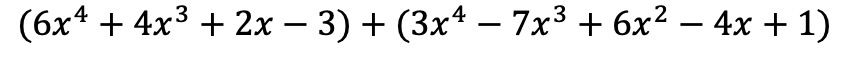
现在我们添加具有相同字面部分的项,即具有相同变量(字母)和相同指数的项。不能添加不相似的术语。
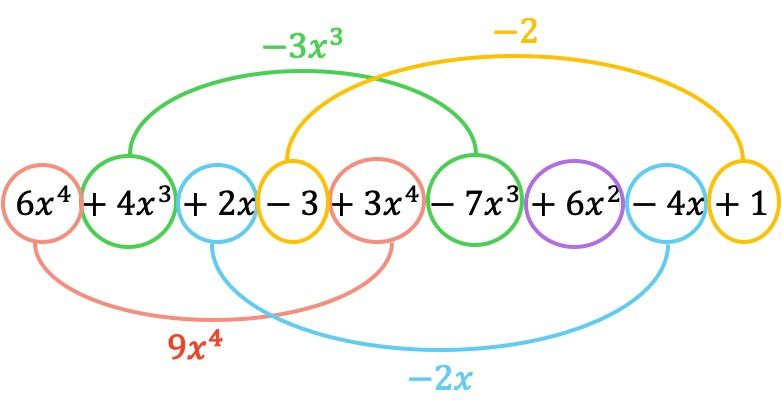
因此,相加所得的多项式为:

正如您所看到的,我们使用两种方法得到了相同的结果,因此在添加多项式时,您可以使用最适合您的一种。
解决了多项式相加的问题
为了方便您进行练习,我们为您提供了几个已解决的多项式和的练习。如果您有任何疑问,可以在页面评论中提问,我们会尽快解答。
练习1
添加以下两个多项式:
![]()
![]()
在本例中,我们将两个多项式垂直相加。为此,我们按次数对多项式进行排序,并将位于同一列的单项式相加:
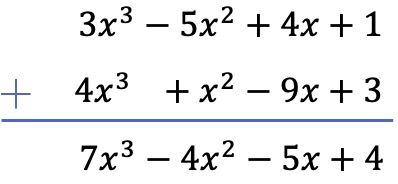
练习2
求解以下两个多项式的和:
![]()
![]()
我们将使用垂直方法对两个多项式求和。因此,我们按次数对多项式进行排序,并将位于同一列中的项相加:
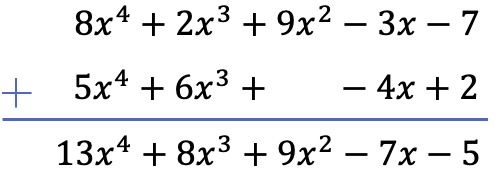
请注意,在这种特殊情况下,第二个多项式的 2 次列中必须保留空格,因为它没有二次项。
练习3
下面两个多项式的和是多少?
![]()
![]()
我们将使用垂直方法执行两个多项式的加法。所以:
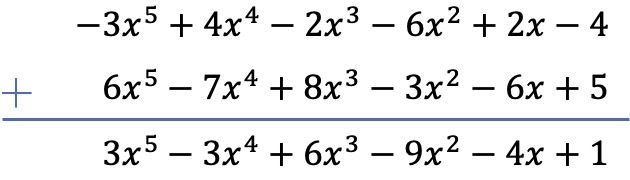
练习4
计算以下三个多项式的总和:
![]()
![]()
![]()
我们将使用垂直方法计算 3 个多项式的总和。因此,我们将多项式按次数排序,并添加位于同一列中的项:
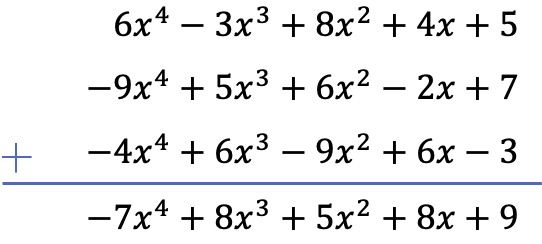
👉👉👉现在您已经了解了两个多项式如何相加,您可能对多项式的另一个特征运算感兴趣:公因子。从多项式中提取公因数非常复杂(并且难以理解),事实上,这样做时会犯很多错误。这就是为什么我们准备了一个指南,我们一步步解释如何提取公因数,以便您完全理解它,并且在执行此操作时不会出错。单击链接,了解从多项式中提取公因式的技巧。
多项式相加的性质
多项式之和具有以下特点:
- 关联性:将 3 个或更多多项式相加时,多项式如何分组并不重要,因为结果总是相同的。也就是说,验证了以下等式:
![]()
- 交换律:在多项式的加法中,加法的顺序不会改变加法的结果。
![]()
- 中性元素:显然,一个多项式加上任何其他数值为零的多项式等价于第一个多项式。
![]()
- 相反元素:任何多项式与其相反多项式相加的结果始终为零。
![]()
你觉得这个解释怎么样?你觉得这有用吗?您更喜欢哪种多项式相加方法,垂直还是水平?我们在评论中读到了你! 👀