多项式函数 - Mathority

在本文中，您将找到有关多项式函数的非常详细的解释，并附有示例。此外，通过我们最后向您展示的练习，您将能够了解多项式函数在日常生活中的应用。

什么是多项式函数？

多项式函数或多项式函数是由等价于多项式的代数表达式给出的函数。这意味着表达式必须遵循多项式的结构： f(x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a _n x ⁿ ，具体取决于我们将要计算的结构确定我们要处理的多项式函数的类型。这些函数的另一个非常相关的特征是它们的未知数的所有指数都是正整数。

多项式函数的部分

我们可以强调有关这些功能的三个重要要素：

多项式系数：这些是伴随未知数的数字，例如以下项的 3 是一个系数： 3x ² 。应该注意的是，多项式中有多少项，就有多少个系数。
多项式的指数或指数：这些是未知数的幂，例如以下项的 2 是指数： 3x ² 。正如我们已经解释的，在多项式函数的情况下，它们始终为正整数。
多项式的次数：该值相当于组成多项式的所有项中最高次数的指数。对于多项式 f(x) = 3x ² – 4x + 2，次数等于 2。

你怎么知道一个函数是否是多项式？

为了识别一个多项式函数，我们必须看看它是否符合我们刚才谈到的特征。我们首先检查定义函数的表达式是否具有多项式结构： f(x) = a ₀ + a ₁ x + a ₂ x ² + a ₃ x ³ + … + a _n x ⁿ 。然后，我们将检查索引是否为正整数，通过这些简单的步骤，我们将能够确定函数是否为多项式。

多项式函数的类型及示例

接下来，我们将向您展示存在的不同类型的多项式函数，这些函数根据多项式的次数进行分类。此外，您还可以找到每种类型的图形表示示例。通过这些多项式函数的示例，您将能够更好地了解不同类别之间的差异。

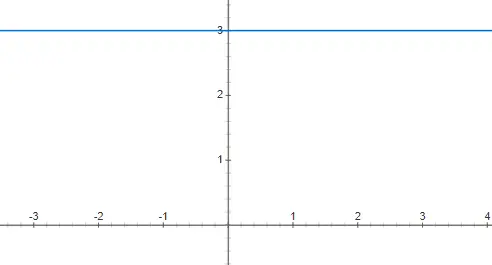
常数函数

常数函数相当于 0 次多项式，这意味着 x 的系数为 0。这就是为什么此类函数不依赖于自变量 x 的值。因此，它的图形表示是一条水平线，它是无限的。您可以在下面找到 f(x) = 3 表示的示例：

一次多项式函数

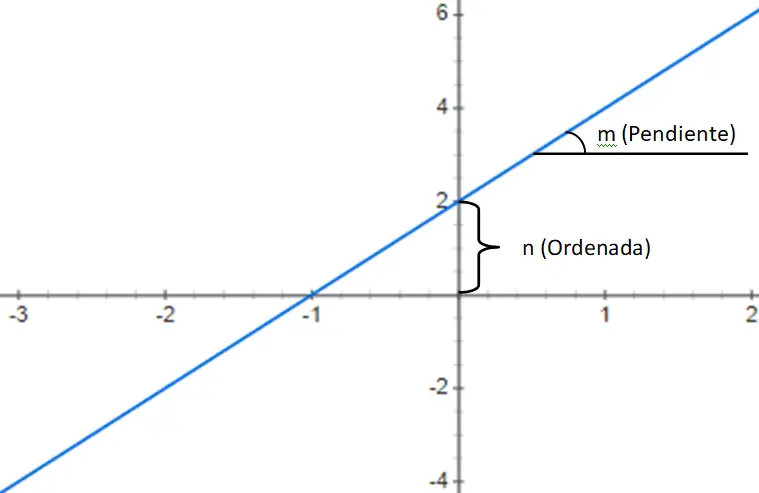
其次，我们找到一阶多项式函数，它由具有以下结构的 1 阶多项式给出：f(x) = mx + n。该表达式由一个称为斜率 (m) 的数字组成，该数字将变量 xy 乘以常数 (n)，然后将其添加到该乘积中。因此，根据 m 和 n 的值，我们可以识别三种不同类型的函数：

仿射函数：该子类型的特点是n的值不等于0，即计算机的值不等于0。因此，该类型函数不经过点(0, 0)，也称为起源。另请注意，如果 m < 0，函数将递减，而如果 m > 0，函数将递增。
线性函数：这些函数与仿射函数的唯一区别是 n = 0，因此它们没有计算机。因此，线性函数的表达式等价于 f(x) = mx。这种类型很容易表示，因为它总是经过点 (0, 0)，并且从斜率我们已经获得了图形。
恒等函数：最后一种类型是线性函数的子群，其中 an = 0 且 m = 1。这意味着表达式仍然是 f(x) = x，其中图形表示是与形成 45° 角的对角线轴之一。此类函数也经过原点 (0, 0)。

下面是一次多项式函数的示例，更准确地说是仿射函数 f(x) = 3x + 2：

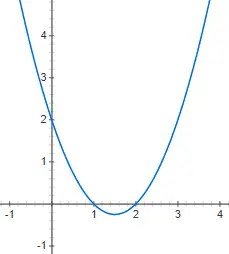
二次函数

二次函数或二次函数用二次多项式表示，其结构如下：f(x) = ax ² + bx + c，其中 a 不等于 0。在这种情况下，图形表示要复杂得多，因为它是不再是一条直线，而是一条垂直的抛物线。您可以在下面找到二次函数 f(x) = 2x ² + 4x – 1 的表示：

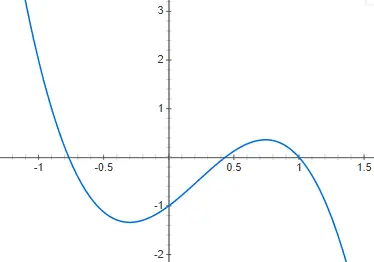
三次函数

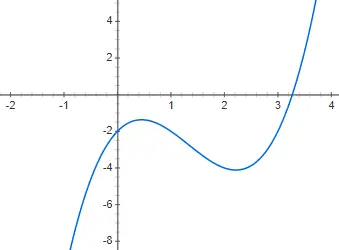
三次函数或三阶函数由三阶多项式给出：f(x) = ax ³ + bx ² + cx + d，与 0 不同。这种类型的函数的表示甚至比是第二度的，因为它可以有几种不同的形式。尽管基本形式（或者至少是最常见的形式）是我们将在以下示例中向您展示的形式，即 f(x) = 2x ³ – 4x ² + 2x – 2：

多项式函数的性质

多项式函数具有一系列区别于其他函数的属性或特征，我们将在下面尽可能清楚地详细说明它们。这样，当你看到这样的函数时，你就会很容易识别它们：

多项式函数的定义域等于所有实数：Dom f = R 或 Dom f = (-∞, ∞)，因此它们在整个实数集上是连续的。
它在Y轴上的交点相当于(0, a ₀ )， ₀是独立项。
沿 X 轴切割次数等于或小于多项式的次数。
多项式函数没有渐近线。
如果所有项的指数均为奇数，则图形关于坐标原点对称，而如果所有项的指数为偶数，则图形关于 OY 轴对称。
这种类型的函数的拐点数量等于或小于 n – 2，其中 n 是次数。
这种类型的函数的相对最大值和最小值的数量等于或小于 n – 1，其中 n 是次数。

如何分析多项式函数？

要分析多项式函数，我们必须遵循分析任何其他函数的相同过程。在下面的列表中，我们总结了必须研究或处理的不同元素：

定义域和范围
与水平轴和垂直轴的交点
单调性（增加和减少、最大值和最小值）
曲率（大于一阶的函数）

显然，我们可以将分析提升到另一个层次并研究许多其他元素，尽管这应该足够了。因为，了解这些元素，您将清楚地了解该函数的外观，并且能够以图形方式表示它。

多项式函数练习

接下来，我们为您提供一系列练习来练习表示函数，特别是多项式函数。这样您将巩固本文中解释的所有概念：

练习1

画出下面的一次多项式函数 f(x) = x + 2 并说出它是什么类型：

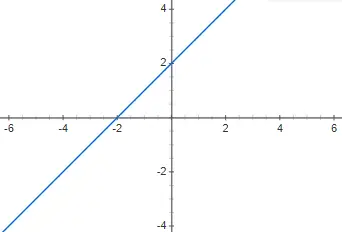
它是一次仿射多项式函数，因为它不等于 0，并且 m 不等于 0。

练习2

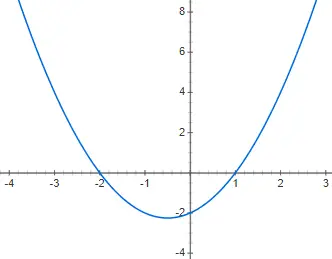
绘制以下二次多项式函数 f(x) = x ² + x – 2 的图像：

练习3

绘制以下三次多项式函数 f(x) = x ² + x – 2 的图像：