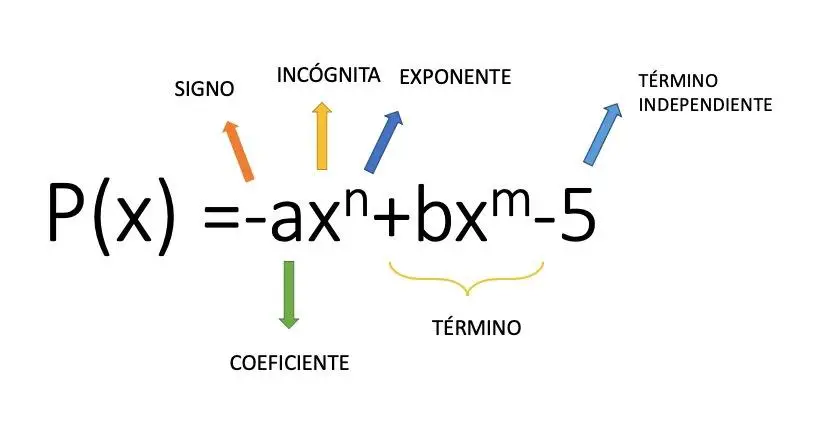
单项式是由变量乘以指数的系数(数值)形成的代数表达式,例如表达式 4x² 就是单项式。因此,从这个数学概念,我们得出多项式,它是几个单项式的加法和减法的集合。在上图中,您可以看到由多个单项式组成的多项式结构的示例。
多项式的类型
通过某个单项式的指数,我们可以将多项式分为不同类型。我们可以将这些表达式分为以下几类:一次多项式、二次多项式、三次多项式等。基本上,您需要确定具有最大指数的单项式,并且该单项式将是多项式 的次数。一旦你了解了它,你就可以将它归为我们刚才谈到的类型之一。
多个变量的多项式
此外,还有另一种组织多项式的方法,即根据形成多项式的单项式的数量。例如,如果我们有一个二项式,这将相当于有一个有两项的多项式,如果我们有一个三项式,这将相当于有一个有三项的多项式,等等。所有这些多项式编目方法都有无限多个子类别。由于这些表达式可以由我们想要的任何单项式组成,并且也可以具有任何次数。
多项式的特征和性质
- 多项式的绝对次数:在上一节中,我们讨论了相对次数的定义。但对于由多个变量形成的多项式,我们的绝对次数等于该单项式所有变量的指数的最大和。例如,在单项式 5x2y3 中,绝对次数等于 2 + 3 = 5。
- 有序多项式:当变量的指数按升序或降序排列时,我们定义关于该变量的有序多项式。例如,如果我们找到这个多项式 P(x) = 3x + 4×3 – x2,在这种情况下它不会被排序。所以,我们应该纠正它,我们会得到这个结果:P(x) = 4×3 – x2 + 3x。
- 完全多项式:当我们找到一个包含所有可能指数(从最高次到独立项)的单项式的多项式时,我们说它是一个完全多项式。例如,以下表达式:P(x) = 3 x² + 2x – 4 就是这种类型,因为 2 和 0 之间不存在缺失的指数。
- 齐次多项式:是每个单项式的绝对次数相等的多项式。变量的指数可以有不同的值,但所有单项式中变量的指数之和必须相同。例如:P(x) = x²y³z + 3 x 4 yz,这两个和得到六个 2 + 3 + 1 = 4 + 1 + 1 = 6。
- 相同的多项式:当我们找到两个或多个共享相同项的系数的多项式时,我们会说它们是相同的多项式。下面您可以看到两个多项式之间的示例:P(x) = 2x + 27 和 Q(x) = 5 (x + 3) – 3 (x – 4),它们是相同的,因为它们共享每个指数的系数:2x = 5x – 3x 且 27 = 15 + 12。
- 零多项式:该多项式只有零系数(等于零),因此多项式的总值也将为零。多项式 P(x) = 0x3 + 0x2 – 0x – 0 是此类多项式的一个明显示例,但不应将其与 Q(x) = 0 混淆,因为在这种情况下,您形成了一个方程,但它并没有并不意味着 Q(x) 的所有系数都为 0。
多项式的数值
多项式的数值是将这个表达式的变量替换为一个数字所得到的结果。我们只需要像组合运算一样求解这个多项式。接下来,我们将解释可用于获取此类表达式的数值的三种方法。
- 直接替换:当我们直接给出多项式的每个变量对应的值时,我们只需将这些变量替换为这些数字即可。这样,如果我们有多项式 P(x) = 2x² – x + 4,并且我们被告知 x = 3,则该多项式的数值将等于 2 · 3² – 3 + 4 = 19。
- 变量解析:当他们不直接给我们变量的值,但给我们一个等价物时,我们将应用这种情况。例如,P(2) 如果 P(x – 1) = x³ – 2x + 1 为真,那么我们首先求解方程 2 = x – 1 并得到 x = 3。最后,我们必须将 3 代入x,使得 3³ – 2 · 3 + 1 = 22。
- 变量的变化:当我们有一个多项式 P(x) = 4x – 2 并且我们想知道 P(x + 2) 的这个值时。接下来,我们需要将表达式中的所有 x 更改为 a(x+2)。也就是说,让我们看看最后一个解决的示例是什么样子:P (x + 2) = 4 (x + 2) – 2。
多项式运算
下面我们将解释如何用多项式求解四种基本算术运算,始终遵循运算层次结构。在每个部分中,您都会找到一些理论,让您了解如何在每种情况下进行操作,以及一些实际示例。
多项式的加法
要添加多项式,我们必须考虑到它们只能按相似项分组,因此如果我们有多项式 P(x) = 3x³ – x² + 2x – 4 和 Q(x) = 2x² + 3x – 2。因此,为了得到 P(x) + Q(x),我们将两个具有相同指数的多项式的系数相加: P(x) + Q(x) = 3x³ + (-x) ² + 2x²) + ( 2x + 3x) + (-4 -2) = 3x³ + x² + 5x – 6。总而言之,我们可以说我们将每个相似项的系数分组并相加,最后我们用一个多项式表示所有项。
多项式减法
多项式的减法与加法的求解方式相同,唯一的区别显然是符号。然后我们将相似的术语组合在一起,减去并将其全部转换为单个表达式。下面我们将通过一个例子向您展示:P(x) = 5x³ – 2x² + x – 3 和 Q(x) = 3x² + 5x + 4,则 P(x) – Q(x ) = 5x³ + (-2x² + 3x²) + (x + 5x) + (-3 + 4) = 5x³ + x² + 6x + 1。
多项式乘法
解决这种类型的乘法时,事情可能会变得有点复杂,但如果您遵循我们将告诉您的所有步骤,那么您就会没事的。在这个数学运算中,所有单项式都将与所有其他单项式一起运算,这意味着我们不仅会相乘相似的项。此外,不仅系数会改变,指数也会改变。通过这个例子,您将更好地理解一切:P(x) = 2x² + 3x – 1 和 Q(x) = 2x + 3:
P(x) Q(x) = ( 2x² + 3x –1 )·( 2x + 3 )= 2x² · 2x + 2x² · 3 + 3x · 2x + 3x · 3 + (-1 ) · 2x + (-1 )· 3 = 4×3 + 6×2 + 6×2 + 9x – 2x – 3 = 4×3 + 12×2 + 7x – 3
基本上,我们将多项式每一项的系数乘以第二项的所有系数,然后应用a n · a m = a n+m的幂属性。
多项式除法
最后,我们只需要解释一下如何解决多项式的除法,基本上我们需要应用除法的分配律:(a + b + c) ÷ d = (a ÷ d) + (b ÷ d) + (c ÷ d)。我们还将以下幂属性应用于n ÷ a m = a nm 。现在我们通过一个简单的例子来了解这一点:P(x) = 3x³ – 6x² + 9x 和 Q(x) = 3x。
P(x) ÷ Q(x) = ( 3×立方– 6x² +9x ) ÷ 3x =( 3×立方÷ 3x ) + ( 6x² ÷ 3x ) + (9x ÷ 3x ) = x² – 2x + 3
现在您已经了解了如何使用多项式求解所有这些运算,我们希望您知道如何在实践中应用它。但如果您认为情况并非如此,并且您想继续练习一点,那么我们建议您查看本页上的一些已解决的练习。这些将帮助您完成所有这些数学概念的内化。
多项式因式分解
要对多项式进行因式分解,您可以按照最后一个链接中的文章中的说明手动进行,也可以使用Ruffini 计算器进行。如果您想快速完成,我们建议您使用第二个选项,但如果您只是学习如何进行因式分解,那么您最好手动练习。应根据您的情况选择执行此操作的方法。
使用科学计算器求解多项式
当今市场上有许多不同的科学计算器。但如果您正在寻找一款可以求解多项式的廉价计算器,我们推荐Casio FX-991SPX II 。它易于使用,功能强大,功能齐全,非常适合任何初中和高中数学学生。下面我们将简要解释如何使用此模型或类似的卡西欧模型求解这种风格的数学表达式。
您必须首先输入变量的数值,然后按“STO”+变量的字母,例如x。因此,当定义了所有变量后,您只需编写所有变量和所有数字的多项式表达式即可。最后,必须按下等号键,这样您就可以得到相当于多项式数值的结果。