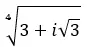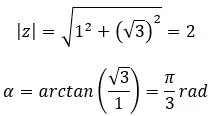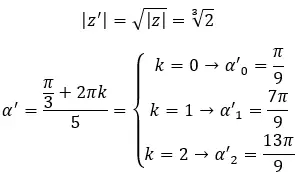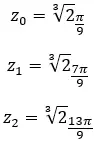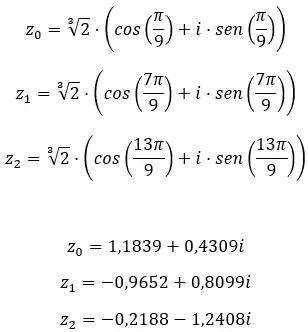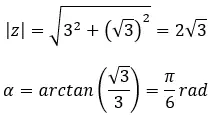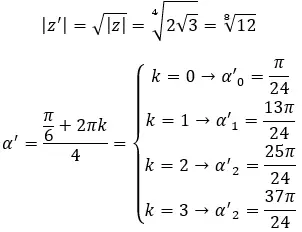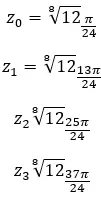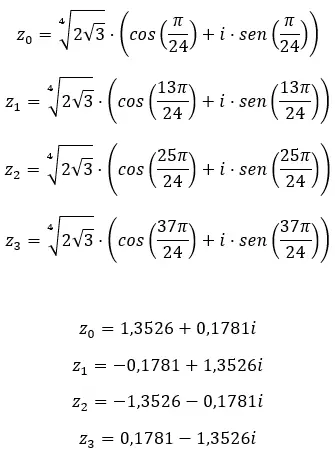计算复数的根非常简单。嗯,一旦你理解了这个过程,你就会发现它是相当重复的。接下来我们会解释它并给你一个例子,这样你就可以学习如何在实际练习中应用它。
复数的 n 次方根
n次根的概念相当于n阶根,因此,计算复数的平方根和五次方根也用同样的方法。当然,解的数量会根据这个顺序而变化。
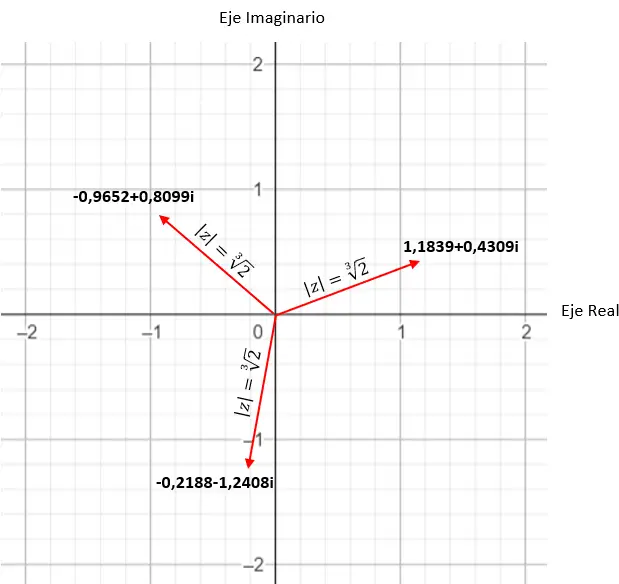
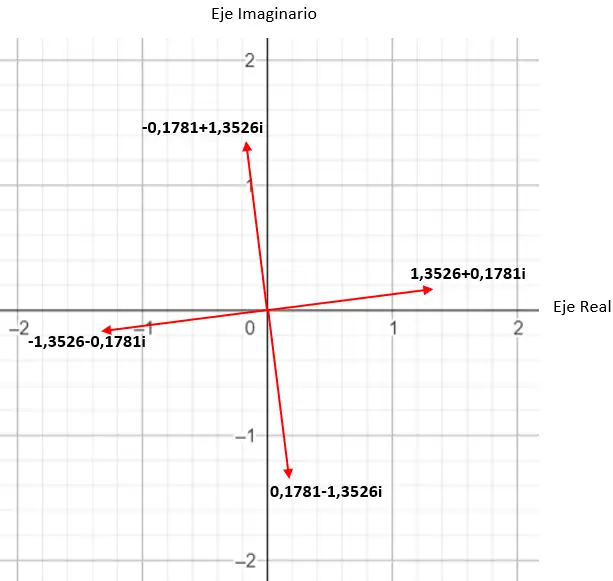
例如,如果我们计算复数的四次方根,我们会得到 4 个不同的解。如果我们用复平面来表达它,我们会看到一个有 4 条边的正多边形形成了,以平面原点为中心。这是一个非常有趣的属性,我们稍后将详细介绍(在示例部分)。
现在我们已经阐明了这个概念,我们将了解如何计算极坐标形式的复数的根(使用这种表示法对于解根来说是最舒服的。)。简单来说,您需要计算模数的根并用 n 表示参数。换句话说,以下复数 (z) 的根:
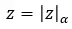
这些金额要计算:
- Module:初始模的第n个根。
- 自变量:在自变量中加上 2πk(以弧度为单位)或 360k(以度为单位),然后除以 n。
在数学上,为了计算模和参数,我们使用以下两个公式:
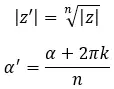
其中,k = 0, 1, 2, …, n-1。
因此,我们将结果表示如下:
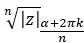
需要明确的是,我们通过求解这个根获得的 n 个解将由相同的模块和 n 个不同的参数形成。
计算复数的 n 次方根的示例
现在我们将看到一些计算复数的 n 次方根的示例。我们建议您尝试自行解决这些问题,完成后查看修复结果。不要忘记上面已经解释了该方法。
求复数的三次方根:1 + i √3 。
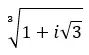
求复数的四次方根:3+i √ 3 。