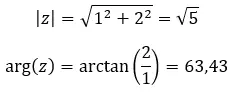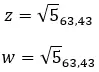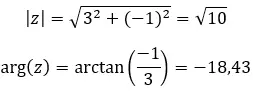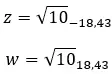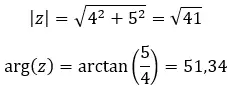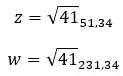在本文中,我们将讨论复数的属性,这些属性在解决计算和简化表达式时非常有用。让我们直接看这些属性。
复数的模数和参数
复数的第一个属性是复数的模和参数。计算起来非常容易,因为您只需要应用几个公式即可。
模数计算公式:

计算参数的公式:

现在,如果该数字以极坐标或三角函数形式表示,则无需进行任何计算。因为,在同一个表达式中,列出了模块和参数。
在下图中,您可以看到极坐标形式的数字公式,其中 |z|是模数,α 是参数。

在另一幅图像中,您可以看到以三角形式表示的数字的结构,其中 |z|是模数,α 是参数。

相等的复数
相等的复数是那些共享模数和参数的数。因此,根据这两个值:

如果满足以下属性,则这些是相同的。
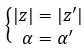
另一方面,如果我们有两个二项式形式的数字,我们可以非常快速且简单地检查它们是否是两个相等的复数。简单来说,必须满足以下表达式:
a + bi = a + bi
我们来看一个例子,判断以下两个复数是否相等:
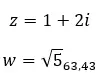
共轭复数
现在让我们继续讨论复数最重要的属性之一,因为知道如何计算复数的共轭对我们解决复杂除法和进行简化有很大帮助。
因此,根据这两个值:

如果它们共享一个模块并且具有相反的参数,我们就说它们是共轭的。因此必须完成:
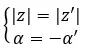
另一方面,如果我们有两个二项式形式的数字,我们可以非常快速且简单地检查它们是否是两个复共轭数。简单来说,必须满足以下表达式:
un + bi = un – bi
我们看一个例子,判断以下两个复数是否共轭:
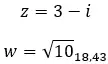
相反的复数
接下来,我们继续看看相反复数的性质。根据这两个值:

如果它们具有相同的模并且它们的参数相差 180 度或 π 弧度,我们可以说它们是相反的:
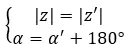
另一方面,如果我们有两个二项式形式的数字,我们可以使用另一种更快、更简单的方法来找出它们是否是两个相反的复数。简单来说,必须满足以下表达式:
a + bi = -a – bi
我们来看一个例子,判断以下两个复数是否相反:
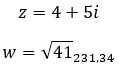
其他属性
显然,这个数字集还有其他属性,例如反复数以及其他一些与基本算术运算直接相关的属性。尽管所有这些都在其他文章中进行了介绍,您可以在下面的列表中看到。