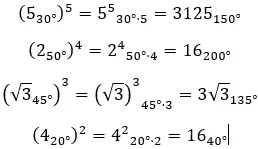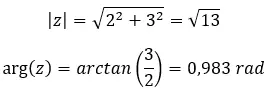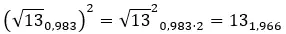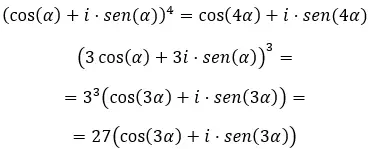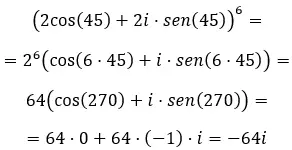如果您知道正确的方法,那么求解复数的幂是一件相当容易的事情。因此,在本文中,我们将解释如何以三种方式求解复数幂:二项式形式、极坐标形式和三角形式的复数。
如何求解复数的幂?
正如我们在简介中所说,使用复杂的权力进行操作时可能会出现三种情况。第一个也是最简单的情况是当我们得到极坐标形式的数字时。第二个是当我们以二项式形式给出数字时,第三个是当我们以三角函数形式给出数字时。
换句话说,当使用极性形式的复合物进行操作时,可以更快地解决练习。因此,建议将相关数字转换为极坐标形式。但其实,一切方法都很容易解决。也就是说,我们将向您解释所有案例的解决方式,并为您提供练习。
极坐标形式的复数幂
当我们想要求解极坐标形式的复数幂时,我们只需将模数提高到任意并将参数乘以 n 即可。用数学表达,我们得到以下公式:
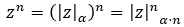
以下是一些示例,您可以尝试自己解决:
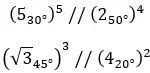
二项式形式的复数幂
另一方面,当我们想要求解二项式形式的复幂时,我们可以使用两种不同的方法。第一个涉及以“代数”方式求解幂(就像 i 是一个变量一样求解)。第二个系统是将二项式形式转换为极坐标形式,然后按照前面的过程进行。
如果您不知道如何从二项式转换为极坐标形式,我们会在有关复数的文章中向您非常清楚地解释。不过,现在我们将通过一个示例快速了解它。
尝试求解以下复数幂: (2 + 3i) 2 。
三角形式的复数幂
最后,当我们想要求解三角形式的复幂时,我们必须使用著名的德莫弗公式。其写法如下:
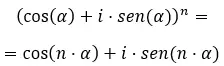
知道这个公式后,尝试解决以下练习: