您可能听说过复数。它们可能是最难处理的一组数字,因为它们结合了实数和虚数。它的统一使得研究无法使用所有实数处理的数值行为成为可能。
什么是复数?
复数是实数和虚数的组合。例如, 4 + 5i是一个复数,其实部等于 4,虚部等于 5i。一般来说,我们可以用下面的公式来表达:
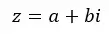
其中,Re(z) = a 且 Im(z) = b
正如我们所说,复数是最大的集合或全局集合,其中包括实数和虚数。接下来,我们向您展示所有集合的层次结构的小图:

因此,当我们有一个实数和一个虚数的组合时,我们就得到了一个复数。但是,有时两个部分之一等于零。在这些情况下会发生什么?好吧,我们仍在处理复数,因为复数集包含所有其他数值集。但是,我们进入一个不同的子类别:
| 复数 | 皇家派对 | 想象部分 | 子类别 |
| 2+5i | 2 | 5i | 复杂的 |
| 4 | 4 | 0 | 纯粹的皇家 |
| 3i | 0 | 3i | 纯粹的想象 |
当我们有一个纯实数时,由于虚数 b 等于 0,剩余的复数相当于:
z = a + 0i = a
另一方面,当我们有纯粹的想象时,a 等于 0,因此,复数仍然如下:
z = 0 + bi = bi
复数的图形表示
为了表示复数,我们使用复平面。它由两条线组成:实线和虚线。这两条数轴用于以图形方式定位每组中的数字,如果我们将它们放在一起,我们会得到一个计划,例如:

X 轴称为实轴,因为它是实部值所在的位置。而Y轴称为虚轴,这是写入虚值的地方。让我们看一个例子,我们将把数字3 + 2i放在复平面上。

正如您在图像中看到的,我们使用数字 3 和 2 作为坐标(每个坐标轴)来定位数字。如果您想了解有关复数表示的更多信息,我们建议您阅读本文。
复数有哪些类型?
现在我们将看到表达复数的方法。到目前为止,我们只看到了基本形式(称为二项式形式),它被写成和:实部加虚部。
但实际上,我们有三种形式:二项式、极坐标和三角式。每种类型的表达式都有其属性并在一种情况或另一种情况下使用。因此,我们将解释所有这些,并展示如何从一种过渡到另一种。
1. 二项式形式
二项式形式的复数写为实部和虚部之和:a + bi。例如,数字 6 + i 是用二项式表示法表示的复数。在这个例子中,公式总是相同的:

因此,要以二项式形式表达一个复数,只需知道它的实值和虚值即可。
例如,值3 + 2i是二项式形式,正如我们之前看到的,它表示如下:

二项式形式主要用于解决复数的加法和减法。
2. 极坐标形式
为了以极坐标形式表达复数,我们必须计算它们的模 |z|和他的论点。极坐标形式主要用于当我们需要解决复数的乘法和除法时。
要计算复数的模,只需计算 a 和 b 的模,如下式所示:

为了计算 z 的幅角或角度,我们需要计算 a 之间 b 的反正切:

需要注意的是,为了准确确定角度α的值,需要确定它位于哪个象限。事实上,反正切函数仅计算 π/2 和 -π/2 之间的角度。要指定复数位于哪个象限,我们必须查看值 a 和 b(如果它们是正数还是负数):
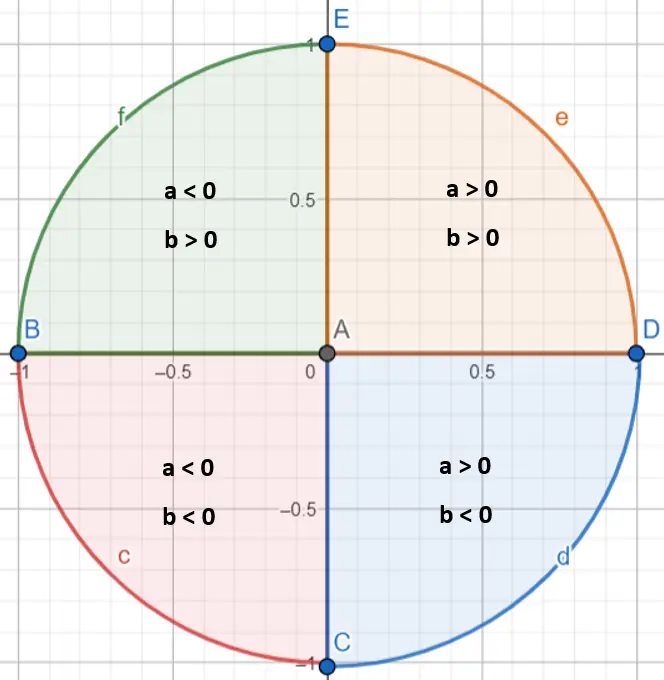
一旦我们知道我们的数字属于哪个象限,我们就需要遵循一些规则:
- 如果复数位于第一象限(a > 0 且 b > 0),我们将保留参数不变。
- 如果复数位于第二象限(a < 0 且 b > 0),我们将在参数中添加 π。
- 如果复数位于第三象限(a < 0 且 b < 0),我们从参数中减去 π。
- 如果复数位于第四象限(a > 0 且 b < 0),我们将在参数中添加 2π。
如果您不知道当我们说象限时我们在说什么,我们建议您查阅我们有关三角比率的文章。
一旦我们知道了 z 的大小和参数,我们就可以用极坐标形式表达复数。尽管此形式接受多种术语,但主要的两个是:

例如,如果我们想将数字3 + 5i更改为极坐标,我们只需按照以下步骤操作即可。
我们首先计算模:
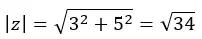
然后我们计算参数,该参数位于第一象限,因此它保持我们计算时的样子。
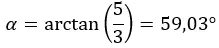
我们用极坐标形式表示该数:
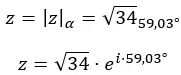
其图形表示如下:
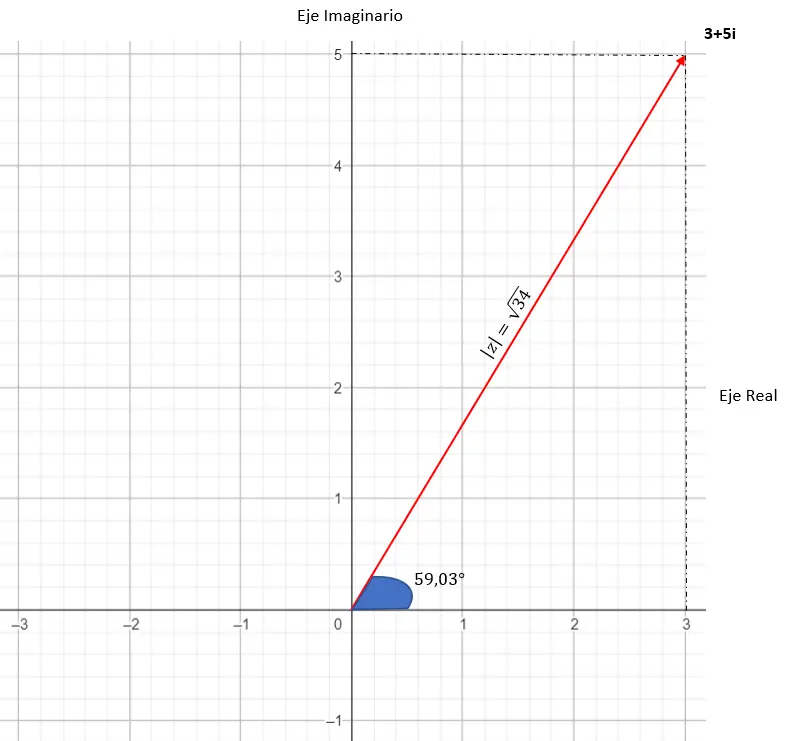
3. 三角函数形式
最后,我们有三角符号,它是根据欧拉公式计算得出的:

例如,要以三角形式表示数字 4 – 3i,我们遵循以下过程:
我们首先使用极坐标形式部分中使用的公式计算模数和参数。
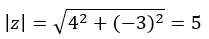
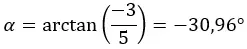
注意:参数位于第四象限,因为 (a > 0 且 b < 0)。
我们将数据以三角形式添加到方程中。
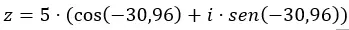
我们已经有了以三角形式表示的数字。其图形表示如下。
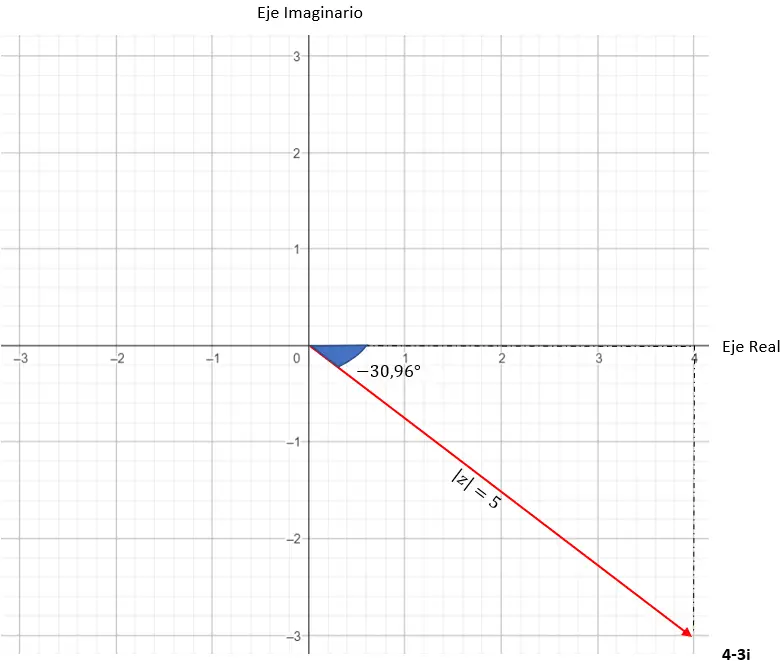
如何从一种类型切换到另一种类型?
您现在已经知道了表达复数的所有方法。在上一节中,您已经了解了如何访问每个表单,但在结束之前,我们想快速总结一下如何从一种表单转换为另一种表单。只是您必须使用我们在上一节中看到的公式。
从二项式到极坐标形式,反之亦然
为了从二项式到极坐标,我们提出下图:
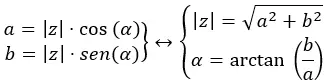
我们之前看到了一个从二项式到极坐标的示例,所以现在我们将使用上图从极坐标到二项式。我们需要将√41 38.66转换为二项式。
我们首先计算a。
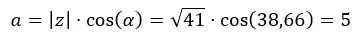
然后我们计算b。
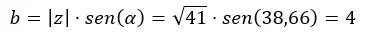
我们用二项式的形式来表达它。
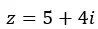
该数字的图形表示如下:
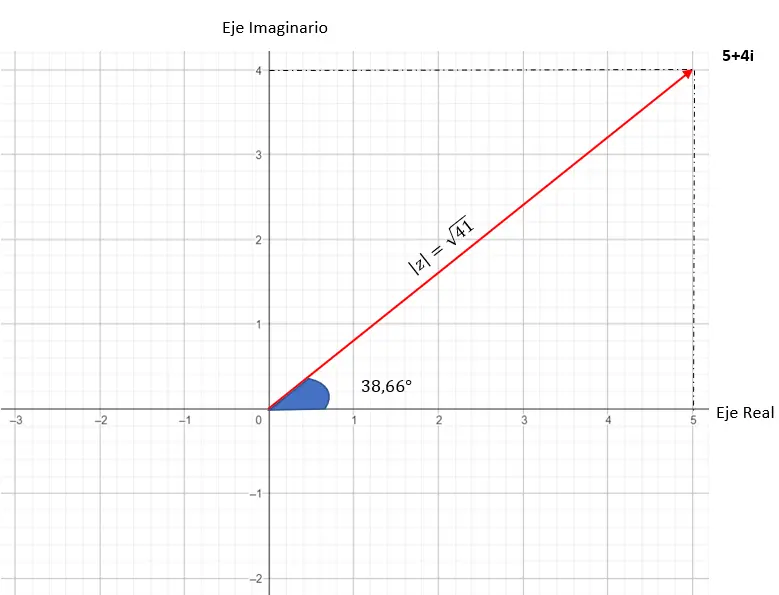
从二项式到三角式,反之亦然
要从二项式转换为三角函数,您还必须应用我们在上一节中讨论的公式。这样,我们首先计算模数和参数,然后将这些数据代入三角形式的方程中。举个例子,我们将通过三角函数传递数字z = 3 + 2i 。
我们首先计算模数和参数。
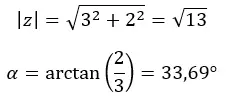
注意:参数位于第一象限,因为 (a > 0 且 b > 0)。
然后,我们用这些数据完成三角形式方程。
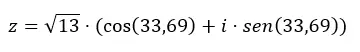
如果我们想从三角函数转到二项式,我们所要做的就是求解前面的表达式。
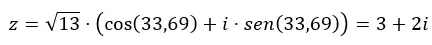
从极坐标形式到三角形式,反之亦然
最后,我们将从极坐标形式转向三角形式。这非常简单,因为这两种形式由相同的两个值表示: modulo 和 argument 。因此,您只需填写表格即可。
举个例子,我们将数字z = √85 12.53转换为三角函数形式。
我们重新表述三角形式方程中的两个变量(模和参数):
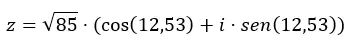
现在您已经知道如何从一种形式过渡到另一种形式,我们建议您通过一些练习进行一些练习。这样你就会巩固本文学到的知识。如果您对此主题有任何疑问,请随时在评论中留下。如果您想了解有关复数的更多信息,请查看下面的链接。