复数是由实数和虚数组成的集合。最后两个数字集可以使用实线和虚线以图形方式表示。当我们将两条线放在同一平面上时,就形成了众所周知的复平面。
复杂的计划是什么?
复平面由相当于实线的实轴(X 轴)和概念化虚线的虚轴(Y 轴)形成。
应该注意的是,这个计划包括所有复数。因此,无论多小或多小,或者复数以什么形式书写,都可以在平面图上用图形表示出来。那么让我们看看这些数字在复平面中是如何表示的。
如何在复平面上绘制复数图形?
我们已经知道(或者如果您不知道,我们建议您阅读我们关于复数的文章),复数有三种写法:二项式形式、极坐标形式和三角形式。每种都根据不同的结构来表达复数值,因此制作图形表示所遵循的方法是不同的。
接下来,我们解释一下三种情况下应遵循的程序:
以二项式形式表示
当我们有一个最常见的二项式表示法的复数时,我们必须查看该数字的结构:

其中a是实部,b是虚部。
知道了这一点,我们就可以推断出 a 的值是我们用于横坐标(实轴)的值,b 的值是我们用于计算机(虚轴)的值。通过下面的例子你会更好地理解它。
我们将尝试表示数字:3 + 2i。
首先是画图(注意横轴是实数,纵轴是虚数):

然后,我们在笛卡尔坐标 (x, y) 中定位图形的点,这是我们从复数推导出来的。在这个实际例子中,我们的点是(3, 2)。
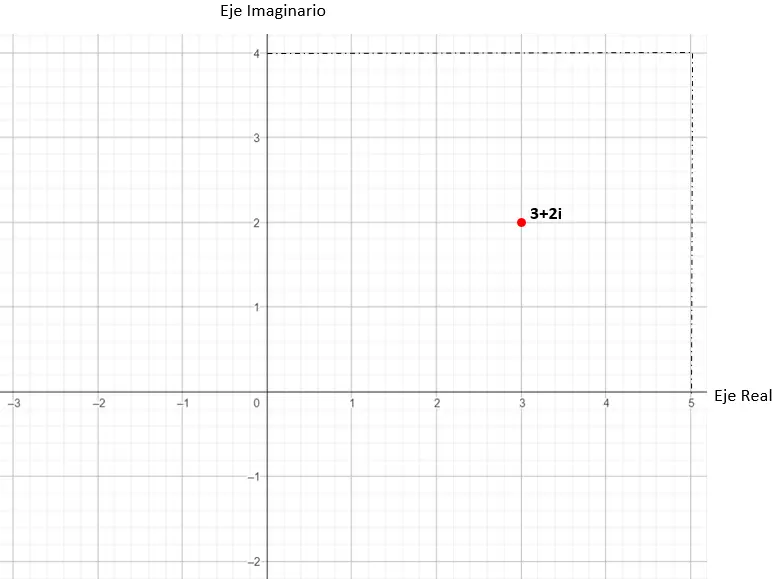
因此,值 3 + 2i 将在复平面中表示。
以极坐标形式表示
现在我们将了解如何用极坐标形式表示复数。要完全理解此方法,您需要知道极坐标表示法根据模块和参数定义复数。在图形表示中使用极坐标(而不是笛卡尔坐标!)。
而极坐标系的主要特点是通过向量和角度来描述点的位置(不像以前的方法)。对应于复数的模和参数。接下来,我们向您展示复数极坐标形式的通用公式:

其中 |z|是模数,α 是参数。这两个变量在计划中的翻译如下:
- 模块:它是定义向量的长度(在原点和相当于我们数字的点之间)。
- 参数:向量与 X 轴的角度。
因此,复数的模对应于我们用来制作图形的向量的长度。而复数的参数或角度是向量与 X 轴之间的角度。下面您可以看到放置所有变量的图表:
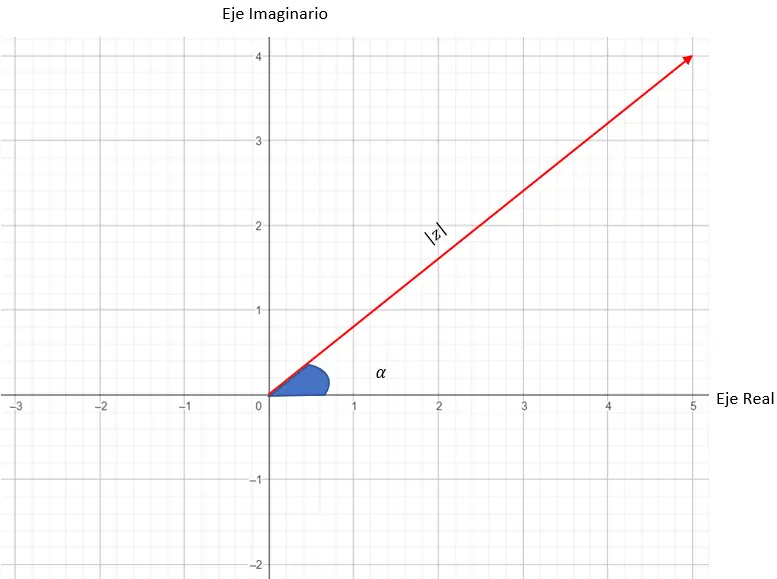
现在我们将尝试表示数字: 3 45 。
首先,我们需要识别模块和参数:
- 模块: 3。
- 角度: 45 度。
接下来我们需要找到图上模数等于 3 的点,在这种情况下,半径为 3 的圆上的任何点都可以。
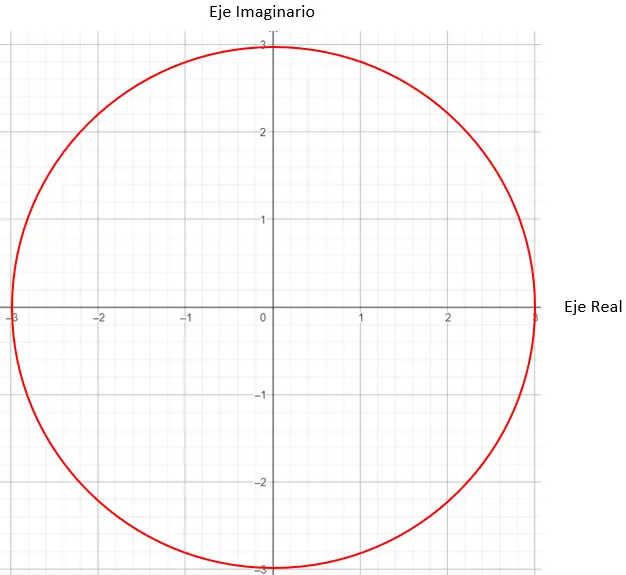
而要完成确定精确点是什么,我们必须提出一个条件:模块生成的向量与原点必须与 X 轴成 45 度角。
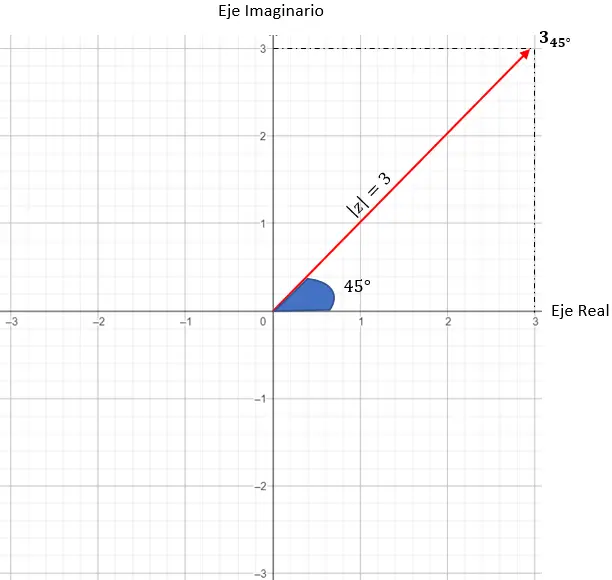
我们已经有了一个用极坐标表示法表示的复数。
以三角函数形式表示
最后,我们还是要解释一下复数是如何用三角函数形式表示的。这种情况和前一种情况实际上是相同的,因为极坐标形式和三角形式使用相同的数据来表示复数:模数和参数。这只改变了表达式的结构:

其中,|z|是模数,α 是参数。
因此,我们必须利用与前一种情况相同的方法:使用模作为“长度”,使用参数作为角度。通过看下面的例子,你会更好地理解它。
我们将表示 z = 4 · (cos (45) + i · sin(45))。
首先是识别模块和角度:
- 模块: 4。
- 角度: 45 度。
接下来,我们需要找到图上模数等于 4 的点,在这种情况下,半径为 4 的圆上的任何点都可以。
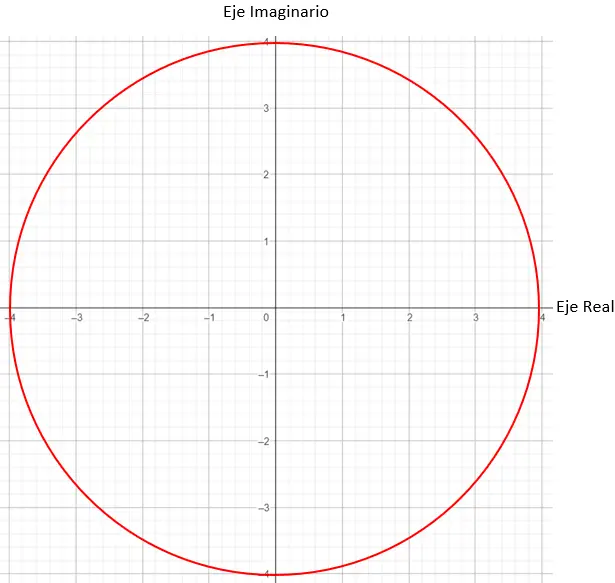
最后,我们找到精确的点,要求模向量与 X 轴之间形成的角度为 45 度,正如参数告诉我们的那样。
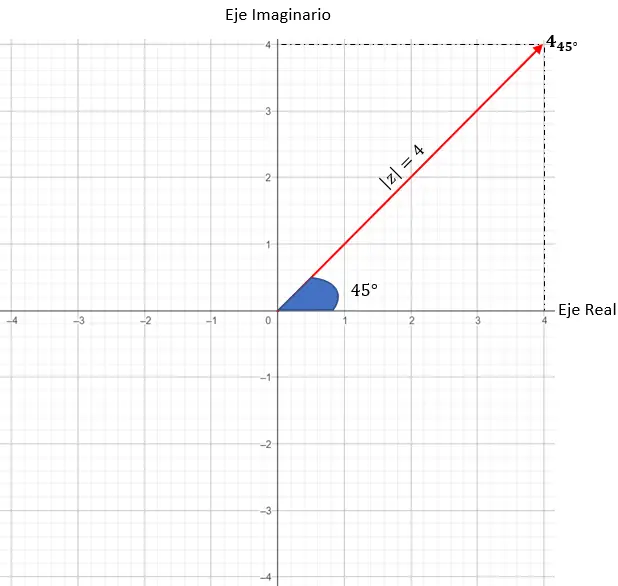
所以我们用三角形式表示一个复数。
复杂的飞机演习
为了结束本出版物,我们将提供最后一个练习。我们强烈建议您解决它,因为这样您将巩固本文中解释的知识。
以下三个复数在复平面上的图形表示的证明:
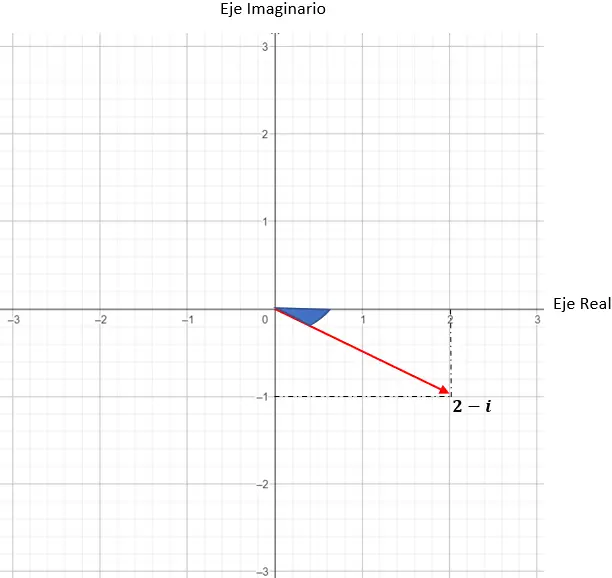
z = 2 – 我
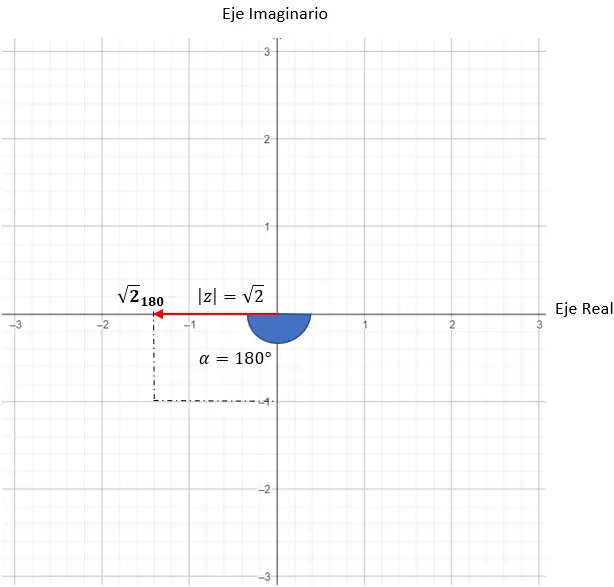
w = √2180
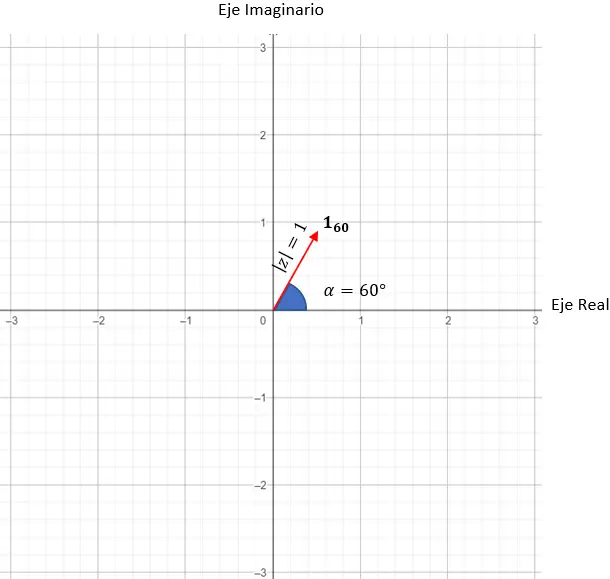
p = cos(60) + I sin(60)