在本页中,我们将解释塔塔利亚三角形(也称为帕斯卡三角形)是什么。我们学习如何以数学方式构造塔塔利亚(或帕斯卡)三角形,以及它的用途和所有属性。最后,我们将展示这个非常重要的三角形是如何以及何时形成的。
什么是塔塔利亚(或帕斯卡)三角形?
塔塔利亚三角形,也称为帕斯卡三角形,是有序整数的三角形形式的数学表示。塔塔利亚(或帕斯卡)三角形用于进行数学计算。
这是塔塔利亚或帕斯卡三角形的定义,但您肯定可以通过三角形的图像更好地理解这个概念:
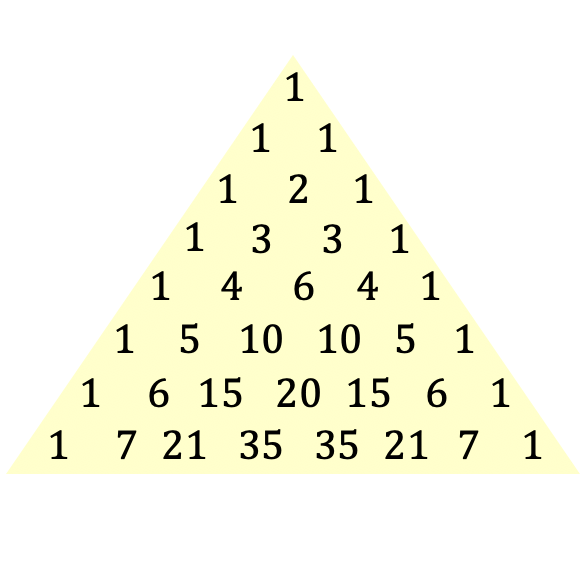
塔塔利亚三角形也被称为帕斯卡三角形,以法国哲学家和数学家布莱斯·帕斯卡 (Blaise Pascal) 的名字命名,他于 1654 年引入了这个三角形表达式,尽管这个三角形自古以来就已为人所知。下面,我们将深入研究这个特定三角形的历史。
塔塔利亚三角形或帕斯卡三角形是如何构造的?
正如您在帕斯卡三角形(或塔塔利亚)中看到的那样,有很多数字,但这并不意味着我们必须记住它们(谢天谢地)。有一个公式可以让你轻松找到帕斯卡或塔塔利亚三角形中的所有数字,你只需要解简单的和即可。
要构建塔塔利亚或帕斯卡三角形,您从三角形的顶部开始,该顶部始终为 1,然后计算下面的线。以下各行中的每个数字都是其正上方两个数字之和,但行尾始终为 1。

因此,您可以计算任意多条塔尔塔利亚三角形的线,因为您可以通过将数字相加来连续添加线。
塔塔利亚三角形或帕斯卡三角形有什么用?
知道如何构造塔塔利亚三角形很好,但是……这个算术三角形有什么用呢?好吧,塔塔利亚(或帕斯卡)三角形在数学中有很多应用,特别是在代数领域。
组合数
首先,塔塔利亚三角形用于直接计算组合数,也称为二项式系数。如果你不知道这些类型的操作是什么,你可以在我们的网站上搜索它们(我们在右上角有一个搜索引擎),因为我们已经写了一篇详细的文章,我们解释了它们是如何解决的,你在那里你还将找到逐步解决的示例和练习。但总而言之,组合数的代数表达式如下:
![]()
那么,所有的组合数都可以用塔塔利亚三角形轻松确定,因为每个二项式系数的解等价于这个三角形表达式的一个数,如下图所示:

例如,组合数
![]()
返回 6,因为塔塔利亚三角形中存在一个 6。
因此,如果您知道如何构造塔塔利亚三角形或帕斯卡三角形,您就可以快速计算任何组合数,而无需使用它们的公式。
牛顿二项式
塔塔利亚(或帕斯卡)三角形的另一个用途是能够计算二项式的幂(单击此链接以了解什么是二项式)。
二项式增强的一个例子是著名的恒等式,例如:
![]()
显着恒等式对于数学来说非常重要,因为它们可以让我们节省大量计算,直接快速地解决复杂的运算。因此,如果您仍然不知道什么是值得注意的身份,我们建议您查看以下链接。
正如您在上一个链接中看到的,著名的乘积可以直接用它们的公式来求解。但是……当这对提升到立方体或更高的程度时会发生什么?
![Rendered by QuickLaTeX.com \begin{array}{c} (a+b)^3 = \ ? \\[3ex] (a+b)^4 = \ ? \\[3ex] (a+b)^5 = \ ? \\[3ex] \bm{\vdots} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5b0a3cca7974eff9ac7a93f3178897c5_l3.png)
好吧,由于二项式定理(或牛顿二项式),这些二项式可以用塔塔利亚三角形以非常简单的方式计算。虽然掌握了方法,但应用起来很快,但要解释清楚,你需要一整页纸。因此,如果您对如何解决此类二项式更感兴趣,请单击链接页面,您可以看到它是如何完成的。
组合学
塔塔利亚三角形或帕斯卡三角形也可用于确定组合和概率。
如果我们遇到需要确定一个组可以组成多少个不同组(无论顺序如何)的问题,我们可以使用塔塔利亚三角形。
例如,如果我们有 5 张牌,要知道有多少种方式可以选择 3,只需转到塔塔利亚三角形的第五行(第一行也是第 0 行)的第三列(第一列为零)即可。该位置的数字 (10) 对应于选择 3 张牌的可能性数量。
![]()
因此,从 5 张牌中,可以形成 10 个不同的组(每组三张牌)。
塔尔塔利亚或帕斯卡三角形的性质
塔塔利亚三角形,也称为帕斯卡三角形,具有以下特点:
- 塔塔利亚(或帕斯卡)三角形是对称的,即将整个三角形分成两个相等的等边三角形的垂直线是对称轴。
- 帕斯卡三角形任意线上所有数字的水平总和等于 2 的幂。

- 塔塔利亚三角形的对角线也很重要:第一条对角线(外对角线)上的数字为一,第二条对角线由所有自然数的序列组成,第三条对角线对应三角形数字,第四条对角线由四方(或四面体)数。
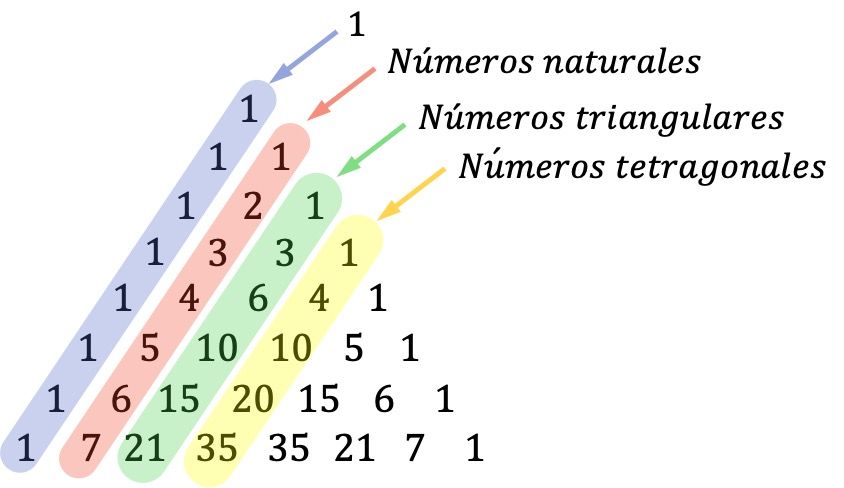
三角形数是可以用三角形表示的数。四方数是那些形成三棱锥的数。
如果你不知道什么是三角形或四边形数,那么什么也不会发生,这只是对塔塔利亚三角形的好奇。但是,您需要了解自然数(用于计算元素的数字)的含义。
- 除数字 1 外,如果一行中的第一个数字是质数,则同一行中的所有数字都可以被该数字整除。例如,在第八行(1-7-21-35-35-21-7-1)中,数字 7、21 和 35 可以被 7 整除(7 是质数)。
- 塔塔利亚三角形的另一个特点是,可以通过以某种方式添加对角线来找到斐波那契数列:
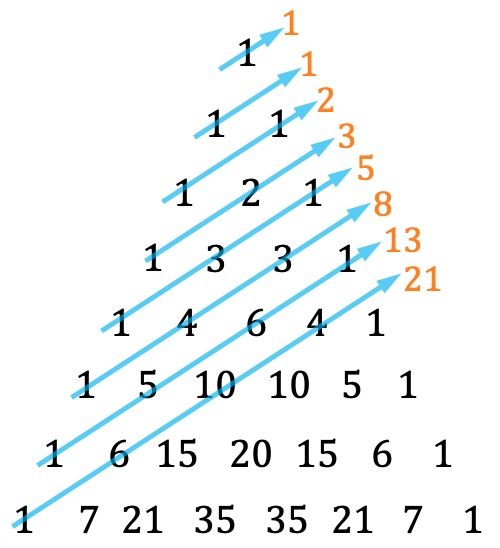
请记住,斐波那契数列的每一项都等于前两项之和,前两项是 1 和 1。因此,属于斐波那契数列的数字是:1、1、2、3、5、8 , 13, 21, 34, 55, 89, 144, 233,…
- 如果我们将帕斯卡三角形第三条对角线的两个连续数字 (1-3-6-10-15-…) 相加,我们将得到一个完全平方数 (1, 4, 9, 16, 25,…)。
- 如果我们把帕斯卡三角形的偶数个涂成一种颜色,奇数个涂上另一种颜色,我们就得到了谢尔宾斯基三角形的图形,这是一个著名的几何集合。下面您可以看到高为 512 的帕斯卡三角形,其中奇数为黑色,偶数为白色:

- Singmaster 猜想指出,每个大于 1 的数字出现的次数是有限的。或者换句话说,尽管塔尔塔利亚三角形的行数是无限的,但除 1 之外的每个数字出现的次数是有限的。令人好奇的是,数字 3003 是迄今为止唯一一个在三角形中出现最多八次的数字。
塔塔利亚或帕斯卡三角的历史
现在我们知道了塔塔利亚三角形是什么样子,让我们看看这个非常特殊的数学三角形是何时发明的。
虽然算术三角形的名字主要归功于著名科学家塔尔塔利亚和帕斯卡,但这个代数三角形以前就已经被使用过。
由二项式系数形成的三角形的第一个记录可以追溯到 10 世纪的印度。然而,波斯人开始研究它的性质,特别是数学家卡拉吉(Al-Karaji,953-1029)和奥马尔·海亚姆(Omar Khayyam,1048-1131)。这就是为什么在伊朗它被称为海亚姆-帕斯卡三角形,甚至简称为海亚姆三角形。
这个三角形在11世纪开始由数学家贾显传入中国,但直到13世纪后期,杨翎才将其作为算术三角形引入。因此,在亚洲国家,他们称之为“杨惠三角” 。
后来,数学三角形通过德国人 Petrus Apianus 传到了欧洲大陆,并于 1527 年在他的《Rechnung》一书中专门发表。从那时起,著名的意大利代数学家尼科洛·丰塔纳·塔尔塔利亚在 16 世纪上半叶深入研究了三角形,为了纪念他,在意大利等国家,该三角形被称为塔塔利亚三角形。
最后,法国人布莱斯·帕斯卡在 1654 年出版的《算术三角形论》中展示了所研究的三角形的许多性质,因此得名帕斯卡三角形。应该指出的是,其中一些性质是已知的,但帕斯卡通过数学归纳法进行了证明。