垂直渐近线 - Mathority

在这里您将找到函数的垂直渐近线是什么（带有示例）。我们还解释了如何找到函数的垂直渐近线，此外，您将能够通过逐步解决的练习进行练习。

什么是垂直渐近线？

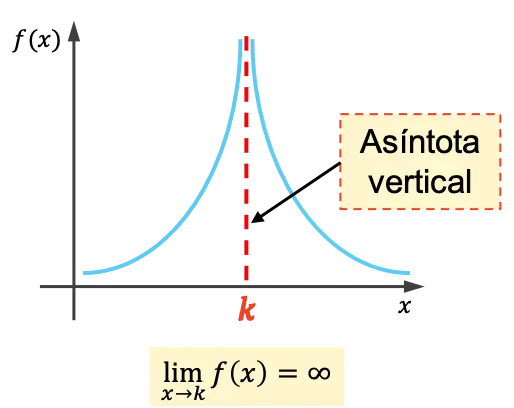
函数的垂直渐近线是一条垂直线，其图形无限逼近而不与其相交。因此，垂直渐近线的方程为x=k ，其中k是垂直渐近线的值。

也就是说，如果x接近k时函数的极限是无穷大，则k是垂直渐近线。

如何计算函数的垂直渐近线

要计算函数的垂直渐近线，必须遵循以下步骤：

求函数的定义域。如果所有点都在定义域内，则该函数没有垂直渐近线。
计算函数在域外的点处的极限。
函数的垂直渐近线将是极限为无穷大的所有值。

请注意，一个函数可以有多个垂直渐近线。例如，正切函数的图像有无穷多个垂直渐近线。

➤参见：正切函数的特征

垂直渐近线示例

作为示例，我们将找到以下有理函数的所有渐近线，以便您可以了解它是如何完成的：

$f(x)=\cfrac{1}{x-2}$

一般来说，存在垂直渐近线的点不属于函数的定义域。因此，我们首先要计算函数的定义域。

这是一个有理函数，因此我们通过观察分母何时消失来确定不属于该域的点：

$x-2=0$

$x=2$

因此，函数的定义域除 x=2 外均为实数：

$\text{Dom } f = \mathbb{R} - \{2\}$

所以x=2 可能是函数的垂直渐近线。为了验证这一点，我们必须计算此时函数的极限：

$\displaystyle \lim_{x \to 2} \frac{1}{x-2}=\frac{1}{2-2}=\frac{1}{0}=\infty$

在这种情况下，我们已经获得了零之间的数字的不确定性，因此，为了求解极限，我们必须计算横向极限，以确定它是正无穷大、负无穷大还是极限不存在。然而，当我们计算垂直渐近线时，我们不需要做横向极限，但获得这个不确定性就足以说明它是垂直渐近线。

简而言之，由于当 x 接近 2 时函数的极限给出无穷大，因此 x=2 是垂直渐近线。

下面是以图形方式表示的函数。正如您所看到的，它非常接近 x=2 线（从左侧和右侧），但它永远不会与它相交，因为它是一条垂直渐近线：

此外，我们还可以从图中推导出函数在 x=2 处的横向极限：

$\displaystyle \lim_{x \to 2^-} \frac{1}{x-2} = -\infty \qquad \lim_{x \to 2^+} \frac{1}{x-2} = +\infty$

解决了垂直渐近线问题

练习1

计算以下有理函数的垂直渐近线：

$\displaystyle f(x)=\frac{3x-1}{2x-1}$

查看解决方案

没有计算函数垂直渐近线的公式，但您必须找到函数的域，并查看在函数未定义的哪些点处极限给出无穷大。

因此，我们将有理函数的分母设置为0来查找不属于域的点：

$2x -1 =0$

$2x= 1$

$x = \cfrac{1}{2}$

因此，函数的定义域除 x=1/2 外均为实数：

$\text{Dom } f = \mathbb{R} - \left\{ \cfrac{1}{2} \right\}$

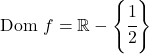
所以 x=1/2 可能是垂直渐近线。为了检查这一点，我们计算此时函数的极限：

$\displaystyle \lim_{x \to \frac{1}{2} } \cfrac{3x-1}{2x-1} = \cfrac{3\cdot\cfrac{1}{2}-1}{2\cdot\cfrac{1}{2}-1} = \cfrac{ \cfrac{3}{2} -1 }{\cfrac{2}{2} -1 } = \cfrac{ \cfrac{1}{2} }{1-1}=\cfrac{\cfrac{1}{2}}{0} =\infty$

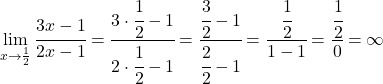
所以x=1/2 是一个垂直渐近线，因为此时函数的极限给出无穷大。

练习2

求以下分数函数的所有垂直渐近线：

$\displaystyle f(x)=\frac{2x+1}{x^2-9}$

查看解决方案

首先，我们将分数的分母设置为零，看看哪些值不在函数的定义域内：

$x^2-9=0$

我们求解不完全二次方程：

$x^2=9$

$x=\pm 3$

因此，有理函数的域是：

$\text{Dom } f = \mathbb{R} - \left\{3, -3\right\}$

因此，为了确定这两个值中哪一个是垂直渐近线，我们求解函数在每个点的极限：

$\displaystyle\lim_{x \to 3}\frac{2x+1}{x^2-9}=\frac{2\cdot3+1}{3^2-9}=\frac{7}{9-9}=\frac{7}{0}=\infty$

$\displaystyle\lim_{x \to -3}\frac{2x+1}{x^2-9}=\frac{2\cdot(-3)+1}{(-3)^2-9}=\frac{-5}{9-9}=\frac{-5}{0}=\infty$

这两个极限给出无穷大，因此x=3 和 x=-3 是问题函数的两个垂直渐近线。

练习3

如果有的话，找到以下有理函数的所有垂直渐近线：

$\displaystyle f(x)=\frac{x+3}{x^2+2x-3}$

➤请参见： 零之间的不确定性

查看解决方案

首先，我们求解二次分母方程，找到抵消分数分母的值：

$x^2+2x-3=0$

$\begin{aligned}\displaystyle x&=\cfrac{-b\pm\sqrt{b^2-4ac}}{2a}=\cfrac{-2\pm\sqrt{2^2-4\cdot1\cdot(-3)}}{2\cdot1}=\\[3ex]\displaystyle &=\cfrac{-2\pm\sqrt{16}}{2}=\cfrac{-2\pm 4}{2}=\begin{cases}\cfrac{-2+4}{2}=1\\[3ex]\cfrac{-2-4}{2}=-3\end{cases}\end{aligned}$

所以函数的定义域是：

$\text{Dom } f = \mathbb{R} - \left\{1, -3\right\}$

因此，我们首先计算函数在 x=1 处的极限：

$\displaystyle\lim_{x \to 1}\frac{x+3}{x^2+2x-3}=\frac{1+3}{1^2+2\cdot 1-3}=\frac{4}{0}=\infty$

另一方面，当 x 趋于 -3 时，我们求解函数的极限：

$\begin{array}{l}\displaystyle\lim_{x \to -3}\frac{x+3}{x^2+2x-3}=\frac{-3+3}{(-3)^2+2\cdot(-3)-3}=\frac{0}{0}=\\[3ex]\displaystyle =\lim_{x \to -3}\frac{\cancel{x+3}}{(x-1)\cancel{(x+3)}}=\lim_{x \to -3}\frac{1}{x-1}=\frac{1}{-3-1}=-\frac{1}{4}\end{array}$

前面的极限给出了零之间的不定形式零，因此为了解决它，我们需要对多项式进行因式分解。如果您对我们如何解决极限有任何疑问，您可以在练习语句的链接中查看如何解决此类不确定性的完整说明。

在这种情况下，只有函数在点 x=1 处的极限给出无穷大，因此x=1 是函数的唯一垂直渐近线。

什么是垂直渐近线？

如何计算函数的垂直渐近线

垂直渐近线示例

解决了垂直渐近线问题

练习1

练习2

练习3

发表评论 取消回复

发表评论取消回复