垂直平面

在此页面上，您将找到什么是垂直平面，如何确定两个平面是否垂直，如何计算垂直平面，垂直平面的示例和已解决的练习，…

什么是两个垂直平面？

在解析几何中，两个平面以直角 (90°) 相交时是垂直的。

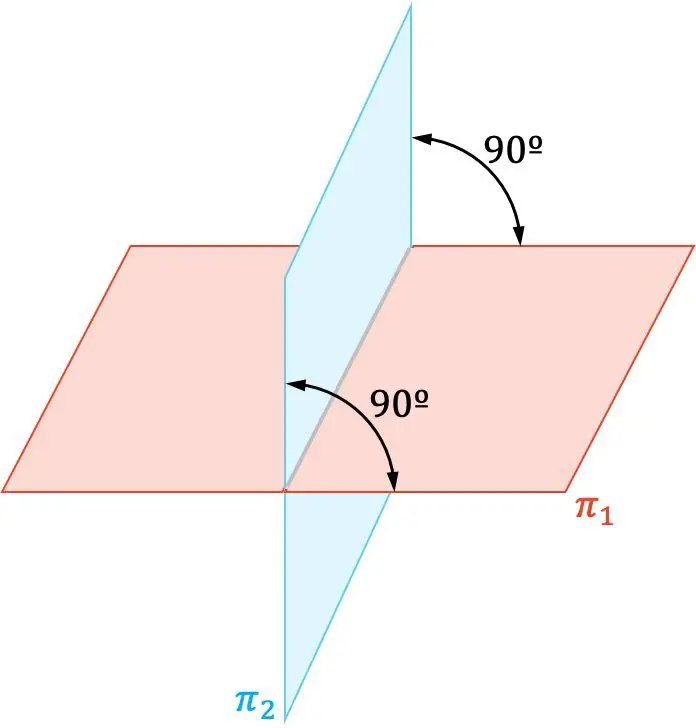
此外，两个垂直平面的法向量也彼此正交。

显然，两个垂直平面之间的距离始终为零，因为它们相交于一条直线。虽然看起来很简单，但两个平面之间的距离概念非常重要，因此如果您对此有任何疑问，我们建议您访问该链接。

另一方面，垂直放置的两个平面并不是平面之间唯一可能的相对位置，因为空间中（在 R3 中）的两个平面也可以相交、平行或重合。

如何知道一个平面是否垂直于另一个平面？

了解了垂直平面的定义后，让我们看看如何知道两个平面是否垂直：

当两个平面的法向量垂直时，它们就垂直。因此，要确定两个平面是否相互垂直，我们必须计算它们的法向量所形成的角度，如果它们形成的角度为 90°，则表示两个平面是垂直的。

因此，要找到两个平面的垂直度，您需要知道如何计算两个向量之间的角度。如果您不记得如何操作，可以查阅链接，您可以在其中找到我们的解释以及确定两个向量之间的角度的必要公式。此外，您将能够看到示例并通过已解决的练习进行练习。

但简而言之，当两个向量的点积为零时，它们是垂直的。因此，当两个平面相关法向量的点积为 0 时，两个平面将是垂直的。

两个垂直平面的示例

例如，让我们检查以下两个平面是否垂直：

垂直于平面的向量的坐标 X、Y、Z 与其一般（或隐式）方程的系数 A、B、C 一致。因此，每个平面的法向量为：

现在我们通过计算法向量之间的点积来检查它们是否是两个垂直平面：

两个法向量之间的点积为 0，因此两个平面相互垂直。

计算垂直于直线的一点的平面

典型的平面和直线问题是求在给定点处垂直于直线的平面的方程。那么，接下来我们通过一个例子来看看它是如何解决的：

• 求垂直于直线的平面的方程。

  

  关于

  

  直截了当地说：

首先，我们需要找到垂直于所讨论的平面的向量。和喜欢直线

垂直于平面，其法向量将与线的方向向量重合。

在这种情况下，该行

是参数方程的形式，所以其方向向量的分量就是参数前面的项

因此，垂直于平面的向量将与直线的方向向量相同：

因此，该计划的隐式（或一般）方程如下：

因此，确定系数 D 的值就足够了。为此，我们将其陈述告诉我们它属于平面的点的坐标代入其方程：

简而言之，平面的笛卡尔方程为：

另一方面，如果您想练习更多关于几何对象之间的垂直度的练习，您可以访问我们的垂直线页面。您将找到有关垂直线所需了解的所有信息：当两条线垂直时、如何计算一条线与另一条线的垂直线、示例、已解决的练习等等。

垂直平面的性质

所有垂直平面都具有以下特征：

• 对称关系：如果一个平面垂直于另一个平面，则该平面也垂直于第一个平面。平行平面也具有该性质。

• 非自反性：显然，没有一个平面可以垂直于自身。

• 定理：在三维 (3D) 空间中，垂直于第三平面的任何一对平面都必须平行。换句话说，如果一个平面垂直于另一个平面并且该平面也垂直于第三平面，则第一个平面和最后一个平面彼此平行。