数字 Pi 是一个数学常数,表示圆的周长与其直径之间的关系。这是一个无理数。换句话说,它不是一个精确的分数。因此,它不能表示为有限的十进制数。 Pi 的值约为 3.14159,用希腊字母 π 表示。
Pi 是数学中的一个重要数字。因此,它在各个领域都有很多应用。例如,它在几何中用于计算面积。此外,还有圆和其他圆形图形的周长。另一方面,在三角学中计算弧的角度和长度。最后,在工程和物理学中计算体积和容量等数量。
每年的 3 月 14 日庆祝圆周率日,因为该日期接近圆周率的值(3.14)。庆祝这个日子是为了纪念圆周率在数学中的作用并提高人们对这个基本常数的兴趣。
谁发现了数字 Pi?
Pi 自古以来就为人所知,希腊数学家阿基米德(公元前 287-212 年)对它进行了精确描述。事实上,他用它来计算几何图形的面积和体积。
18世纪,瑞士数学家约翰·兰伯特证明Pi是一个无理数。后来到了19世纪,德国数学家费迪南德·冯·林德曼解释说Pi是一个超越数。也就是说,它不能表示为具有有理系数的多项式方程的精确解。
纵观历史,不同的数学家为理解圆周率做出了贡献,并开发了更精确的计算技术。今天,Pi 仍然是世界上最重要和最著名的数学常数之一,并且仍然是数学研究的主题。
为什么数 Pi 是无穷大?
Pi 的值约为 3.14159,但实际上它是一个小数点后无限延续的数字。这意味着Pi是一个无限数,不能完全用十进制数表示。
虽然 Pi 的值是无穷大,但实际上可以非常精确地计算出 Pi 的近似值。到目前为止, Pi 的数百万位已经被计算出来,并且已经证明它的十进制数字没有规则的模式。尽管这是通过超级计算机完成的,因为我们无法计算那么多数字。
有哪些方法可以计算数字 Pi 的近似值?
计算 Pi 值的实用方法有几种,接下来我们逐步解释数学家最常用的三种方法。
1.阿基米德法
希腊数学家阿基米德使用几何方法计算了 Pi 的近似值。使用该方法的步骤如下:
1. 画一个圆,并通过圆心画一条线,并在两个相对点处相交,如下所示:
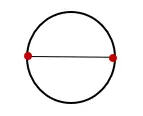
2. 测量与圆相交的线的长度并将其标记为“D”。该测量值就是圆的直径。
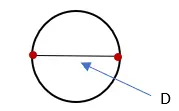
3. 测量形成圆的线的长度并将其标记为“C”。该测量值就是圆的周长。
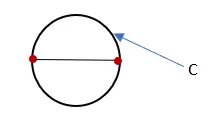
4. 用圆的周长 (C) 除以圆的直径 (D)。结果是 Pi 的近似值。
例如:如果圆的直径为 6,周长为 18,则 Pi 的近似值为 18 ÷ 6 = 3。显然这个示例非常基础,但是如果您使用实际周长的值来进行计算,您将看到该方法工作正常。
事实上,我们建议您尝试一下:测量杯子或圆形物体的尺寸,看看它是否适合您。
2. 蒙特卡罗方法
蒙特卡罗方法是一种用于计算 Pi 近似值的概率方法。为此,在平面上随机生成大量点,并计算适合正方形内接圆的点的数量。该过程的应用如下:
1、在边长为1的正方形内画一个圆,如下图:

2.在正方形内随机生成大量点。
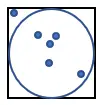
3. 计算适合圆的点的数量。我们称这个数量为“n”。
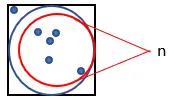
4. 计算生成的总点数。将此数量称为“m”。
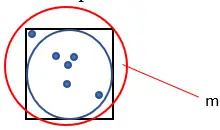
5. 使用以下公式计算 Pi 的近似值:Pi = (4 · n) ÷ m。
例如,如果生成了 380 个点,其中 300 个点适合圆,则 Pi 的近似值为 (4 · 300) ÷ 380 = 3.16。这个值看起来很像 Pi 的前两位小数,但就像前面的方法一样,使用实际测量会给你一个更精确的值。
3、迭代法
迭代法是一种用来计算Pi近似值的数学方法,该方法使用隐含Pi值的公式并迭代应用以提高计算的准确性。以下是使用此方法的步骤:
- 选择Pi的初始值,例如可以选择3。
- 使用涉及 Pi 值的公式来计算新的近似值。例如,您可以使用以下公式:Pi = (Pi + (4 ÷ Pi)) ÷ 2
- 将新的近似值与旧值进行比较。如果两者之间的差异足够小,那么您就得到了准确的结果。如果差异仍然显着,请将新值分配给 Pi 并从步骤 2 开始重复该过程。
例如,如果 Pi 的初始值为 3,则新的近似值为 (3 + (4 ÷ 3)) ÷ 2 = 2.66666666。但是,由于两者之间的差异不是很小,因此您始终可以重复该过程几次才能找到准确的值。
Pi 有哪些应用?
Pi是数学中的一个重要数字,在各个领域都有很多应用。 Pi 最重要的应用包括:
几何学
Pi 在几何中用于计算圆和其他圆形图形的面积和周长:
- 圆:计算圆的面积和周长。
- 球体:确定球体的面积和体积。
- 圆柱体:计算圆柱体的表面积和体积。
- 圆锥体– 用于计算圆锥体的表面积和体积。
三角学
它在三角学中用于计算角度和弧长非常有用。它的一些应用是:
- 角度:角度和弧长的计算。
- 三角函数– 用于计算某些角度的三角函数值。
- 圆三角函数:计算360度角的三角函数值。
工程
在工程中,Pi 用于计算体积和容量等数量。它的一些应用是:
- 电子学:计算电阻和电容等量。
- 电:用于计算功率和电能等量。
- 土木工程:计算结构和建筑构件的表面积和体积等数量。
身体的
数字 Pi (π) 是一个数学常数,在物理学中有许多应用。以下是 Pi 在物理学中的使用的一些示例:
- 波– 用于计算波的频率和波长。
- 力学:在力学中,它对于计算旋转系统中的功和能量很有用。
- 电磁学:在电磁学中,它可用于计算电容器中存储的能量和绕组中的电感。
- 宇宙学在宇宙学中,Pi 用于计算时空曲率和宇宙的膨胀。
Pi在现实生活中有什么应用?
以下是 Pi 在日常生活中如何使用的一些示例:
- 几何:定义圆形垫的面积或测量覆盖圆形桌子周长所需的卷尺长度。
- 烹饪——确定一个平底锅需要多少水或液体,或者一个圆形容器可以容纳多少原料。
- 天文学:了解行星与恒星之间的距离、行星的轨道以及天体在天空中的位置。
- 园艺:了解填满圆形花盆所需的土壤或土壤量,或计算给圆形花园中的植物浇水所需的水量。