因子定理 - 数学

在本页中，我们解释什么是因子定理。此外，我们还展示了因式定理的用途：多项式的整除性、求根、因式分解多项式等。最后，您将能够逐步练习因子定理。

什么是因数定理？

在数学中，因子定理表示，当且仅当 P(a)=0 时，多项式 P(x) 才能被另一个 (xa) 形式的多项式整除。

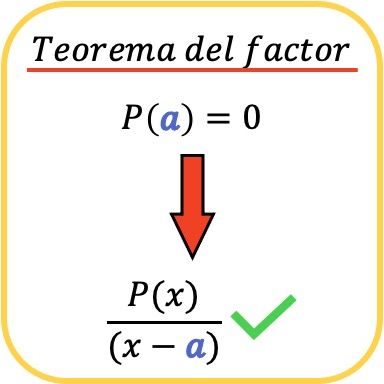
同样，根据因子定理，如果多项式 P(x) 可被 (x−a) 整除，则意味着值 a 是多项式 P( x) 的根（或零））。

一个多项式可被另一个多项式整除意味着两个多项式相除的余数（或余数）等于零。如果您不完全记住这个概念，在下面的链接中您可以看到多项式除法的示例，在那里您还可以找到如何划分多项式的说明以及逐步解决的练习。

因子定理示例

现在我们知道了因子定理的数学定义，让我们看几个例子来看看它是如何应用的。

实施例1

因子定理的一个应用是找出给定的多项式是否可被二项式整除。让我们看一个如何使用因子定理来完成此操作的示例：

确定多项式 P(x) 是否能被二项式 Q(x) 整除，两者均为：

$P(x)=x^2-4x+3 \qquad \qquad Q(x)=x-1$

首先，除数多项式 Q(x) 是 (xa) 类型的多项式，因此我们可以应用因子定理来解决该问题。

因此，为了检查 P(x) 是否可以除以 Q(x)，我们需要计算 x=1 时多项式 P(x) 的数值，因为 1 是除法多项式的独立项，其符号发生了变化:

$\begin{aligned} P(1) & =1^2-4\cdot 1+3 \\[2ex] & = 1-4+3 \\[2ex] & = 0 \end{aligned}$

x = 1 时多项式 P(x) 的数值为零，因此根据因子定理 P(x) 可以被 Q(x) 整除，或者换句话说，两者相除的余数将为空。

我们可以通过将 2 个多项式除以鲁菲尼定理来验证是否满足整除条件：

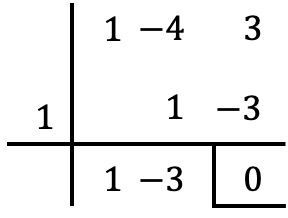
正如您在本例中看到的，因子定理是余数（或余数）定理的特例。我给您留下这篇文章，它解释了余数定理是什么，您还将找到用它解决的示例和练习。而且，更重要的是，您将能够看到余数定理和因子定理之间的区别。

实施例2

因子定理也可用于查找多项式的根（或零点）。但是，显然，要理解此类问题，您需要知道多项式的根是什么。如果你还是不明白这个概念，你可以看一下链接页面，里面有详细的解释。

让我们通过一个例子来看看如何应用因子定理来求多项式的根：

给定多项式 P(x)，计算其根之一是否为 x=2：

$P(x)=x^3-3x^2+5x-6$

应用因子定理，如果 x=2 的 P(x) 数值为零，则 x=2 项将仅是多项式 P(x) 的根。所以我们需要找到这个数值：

$\begin{aligned} P(2) & =2^3-3\cdot 2^2+5\cdot 2-6 \\[2ex] & = 8-3\cdot 4 +5\cdot 2 -6\\[2ex] & = 8-12+10-6 \\[2ex] & = 0\end{aligned}$

事实上，多项式 P(x) 的数值在 x=2 时消失，因此借助因子定理，我们可以断言 x=2 是多项式 P(x) 的根。

使用因子定理对多项式进行因式分解

因子定理的另一个应用是多项式的因子分解。如果您不知道它是什么，因式分解多项式意味着将多项式的表达式转换为因式乘积，即因式分解多项式简化了其代数表达式。

因此，阶乘定理表明，如果多项式 P(x) 对于给定值 a 满足 P(a)=0，则所述多项式的表达式可以分解为乘积 P(x)=(xa)· Q( x)，其中 Q(x) 是多项式 P(x) 除以 (xa) 所得的多项式。

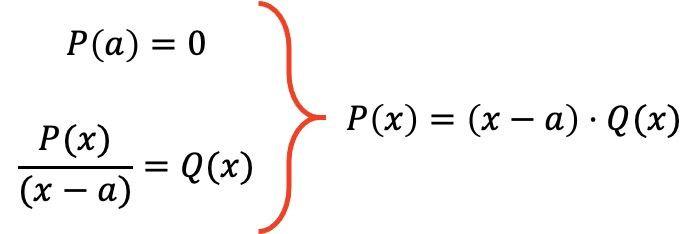
例如，我们将使用阶乘定理对以下多项式进行因式分解：

$P(x)=x^3+2x^2+4x+8$

从前面的多项式中，我们可以知道 x=-2 是它的根之一，因为 x=-2 的多项式的数值等于 0：

$\begin{aligned} P(-2) & =(-2)^3+2\cdot (-2)^2+4\cdot (-2)+8 \\[2ex] & =-8+2\cdot 4+4\cdot (-2)+8 \\[2ex] & = -8+8-8+8 \\[2ex] & = 0 \end{aligned}$

因此，我们用鲁菲尼法则将多项式 P(x) 除以 x 形成的二项式和该根改变符号之间的值，即因子 (x+2)：

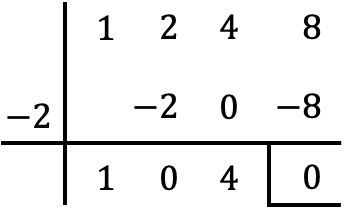
所以多项式除法的商是：

$\cfrac{P(x)}{x+2} =x^2+4$

最后，根据因子定理，我们可以将多项式 P(x) 表示为因子 (x+2) 乘以之前除法得到的商的形式：

$P(x) = (x+2) \cdot (x^2+4)$

因此，我们对多项式 P(x) 进行了因式分解，但只是部分分解。为了完全分解多项式，必须应用更长的过程。我们制作了一份指南，逐步教授如何因式分解鲁菲尼多项式，此外，在本文中，我们解释了所有类型的因式分解，您将能够通过已解决的练习进行练习。因此，请单击链接以了解如何从集合中分解多项式。

已解决的因子定理问题

然后，我们准备了几个关于因数定理一步一步解决的练习题，供大家练习，从而检验自己是否理解了这个定理。我们建议您尝试自己做一下，然后看看您是否正确理解了解决方案。另外不要忘记您可以在下面的评论中向我们留下您的问题！ ❓❓💬💬

练习1

使用阶乘定理来查找多项式 P(x) 是否可以被二项式 Q(x) 整除，如果可以，则找到多项式的根并对其进行因式分解。

$P(x)=2x^3-4x^2+x-7 \qquad \qquad Q(x)=x-3$

查看解决方案

在这种情况下，多项式除数Q(x)是仅由x和独立项组成的二项式。因此，为了证明多项式 P(x) 可以通过阶乘定理除以另一个多项式 Q(x)，我们必须在除数多项式改变符号的独立项中评估多项式 P(x) 的数值，也就是说在 x=3 时：

$\begin{aligned} P(3) & =2\cdot 3^3-4\cdot 3^2+3-7\\[2ex] & = 2\cdot 27-4\cdot 9+3-7 \\[2ex] & = 54-36+3-7\\[2ex] & = 14 \end{aligned}$

x=3处的多项式P(x)的数值相当于14，也就是说它不同于零。因此，根据因子定理，P(x) 不能被 Q(x) 整除，因为除法的余数不为零。

练习2

通过阶乘定理找出多项式 P(x) 是否能被二项式 Q(x) 整除，如果是，则找到多项式 P(x) 的根并对其进行因式分解。

$P(x)=x^3+5x^2+3x-1 \qquad \qquad Q(x)=x+1$

查看解决方案

在这种情况下，多项式除数Q(x)是仅由x和独立项组成的二项式，因此我们可以应用阶乘定理。

为了检查多项式 P(x) 是否可以除以多项式 Q(x)，我们必须找到多项式 Q(x) 改变符号的独立项的多项式 P(x) 的数值，即即，在 x=-1 处：

$\begin{aligned} P(-1) & =(-1)^3+5\cdot (-1)^2+3\cdot (-1)-1\\[2ex] & = -1+5\cdot 1+3\cdot (-1)-1\\[2ex] & = -1+5-3-1\\[2ex] & = 0 \end{aligned}$

在此问题中，x=-1 处多项式的数值为零，因此 P(x) 可被 Q(x) 整除。

那么，我们可以通过阶乘定理推导出x=-1是多项式P(x)的根，因为P(x)在x=-1处的数值消失。

因此，由于 x=-1 是多项式 P(x) 的根，因此要对其进行因式分解，只需将其除以 x+1 即可。为此，我们将使用 Ruffini 方法：

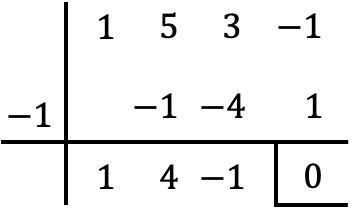
所以运行的结果是：

$x^2+4x-1$

因此，我们可以将多项式 P(x) 因式分解如下：

$P(x) = (x+1) \cdot (x^2+4x-1)$

练习3

使用阶乘定理查找多项式 P(x) 是否可被二项式 Q(x) 整除，如果是，则还查找多项式 P(x) 的根并对其进行因式分解。

$P(x)=x^3+5x^2+4x-6 \qquad \qquad Q(x)=x+3$

查看解决方案

在这种情况下，除Q(x)的多项式是仅由x和独立项构成的二项式，因此我们可以使用因子定理。

为了检查多项式 P(x) 是否可被多项式 Q(x) 整除，我们必须确定多项式 Q(x) 改变符号的独立项的多项式 P(x) 的数值，即 -即 x =-3 时：

$\begin{aligned} P(-3) & =(-3)^3+5\cdot (-3)^2+4\cdot (-3)-6\\[2ex] & = -27+5\cdot 9+4\cdot (-3)-6\\[2ex] & = -27+45-12-6\\[2ex] & = 0 \end{aligned}$

在这种情况下，x=-3 处多项式的数值为零，因此 P(x) 实际上可以被 Q(x) 整除。

因此，我们从阶乘定理推导出 x=-3 是多项式 P(x) 的根，因为 P(-3) 等于 0。

因此，由于 x=-3 是多项式 P(x) 的根，因此要因式分解它，我们必须将其除以 x+3。为此，我们将使用鲁菲尼规则：

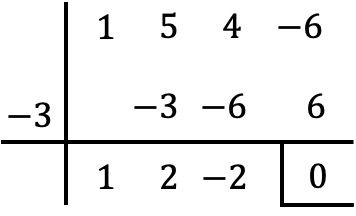
那么除法的结果就是：

$x^2+2x-2$

因此，我们可以通过以下方式对多项式 P(x) 进行因式分解：

$P(x) = (x+3) \cdot (x^2+2x-2)$

您如何看待因子定理？你认为它在代数中有用吗？我们在评论中读到了你！
👀⬇⬇⬇👀

什么是因数定理？

因子定理示例

实施例1

实施例2

使用因子定理对多项式进行因式分解

已解决的因子定理问题

练习1

练习2

练习3

发表评论 取消回复

发表评论取消回复