在此页面上,您将找到向量之间线性组合含义的解释。此外,您将能够看到如何将向量表示为线性组合的示例,此外,您将能够通过练习和逐步解决的问题进行练习。
什么是向量的线性组合?
线性组合的定义如下:
一组向量的线性组合是将组中所有向量乘以标量(实数)相加而得到的向量。
换句话说,给定一组向量
![]()
它们的线性组合是:
![]()
其中系数
![]()
这些是实数。
因此,作为其他向量的线性组合的向量意味着第一个向量可以用第二个向量来表达。
通过在平面上绘制一个向量(两个向量的线性组合)可以更好地理解这个概念:
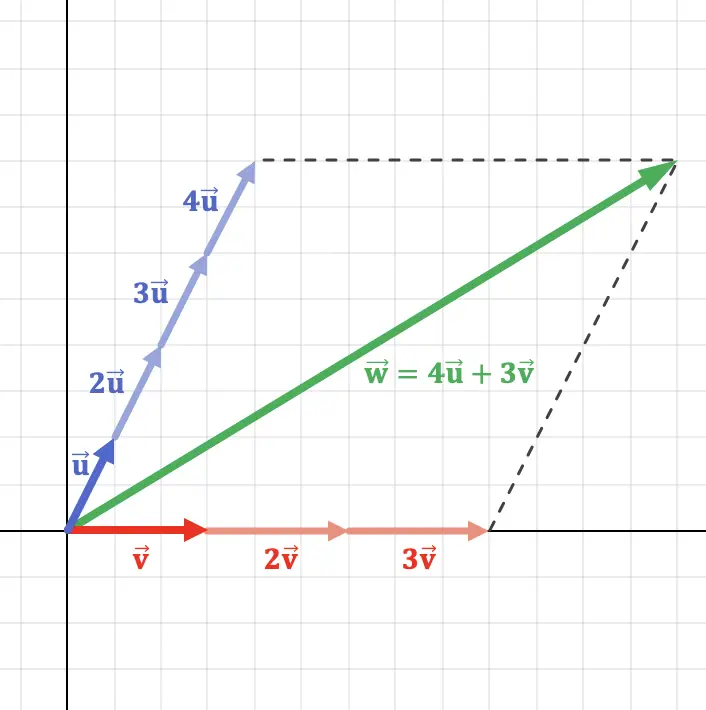
正如您在上面的图形表示中看到的,向量
![]()
可以从向量中获得
![]()
和
![]()
执行向量运算。因此,向量
![]()
是其他两个向量的线性组合。
需要强调的是,这种线性组合是唯一的,或者说,每个向量只有一个可行的线性组合。因为按照前面的例子,如果我们乘以
![]()
对于 6 而不是 4,我们将获得另一个不同的向量。
此外,平面(R2)中线性组合的属性之一是,如果任何向量具有不同的方向,即如果它们不平行,则任何向量都可以作为其他两个向量的线性组合。
另外,有时我们可以通过肉眼识别出两个向量是线性组合。要做到这一点,其组成部分成比例就足够了。例如,以下两个向量的坐标成比例,因此向量是线性组合:
![]()
![Rendered by QuickLaTeX.com \cfrac{3}{1} = \cfrac{6}{2} = \cfrac{-3}{-1} = 3 \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-aac41542948764e158ebe590c6b36e67_l3.png)
最后,无论是在二维(R2 中)还是三维(R3 中)向量空间中,如果一组向量内存在线性组合,则意味着它们彼此线性相关。另一方面,如果向量之间不可能存在线性组合,则意味着它们是线性无关的。
如果您不完全清楚最后一个概念,我们建议您查看我们对线性相关向量和独立向量的解释,在这里您将找到线性相关或独立向量的含义、每种类型的示例以及它们之间的差异。 。这个概念被广泛使用,事实上,它在考试中也经常被问到,所以充分理解它很重要。
如何将向量表示为其他向量的线性组合
然后我们将看到如何解决一个典型的问题,其中要求我们找到向量的线性组合。
- 表达向量
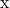
作为线性组合
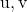
和
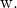
![]()
![]()
使得向量
![]()
是其他向量的线性组合,必须满足以下等式:
![]()
其中系数
![]()
和
![]()
这些都是我们必须找到的未知数。
因此,我们用每个向量的坐标替换它:
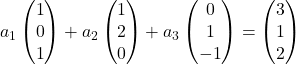
我们将每个向量乘以其系数:
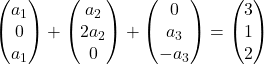
我们添加向量:
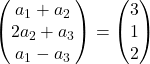
每个左坐标必须等于每个右坐标。因此我们有 3 个方程:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] a_1-a_3 = 2 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e5fe050102a285a325dcd81d07ef5d5_l3.png)
剩下的就是求解所获得的方程组。为此,请使用您喜欢的方法(替换法、克莱默法则、高斯-乔丹法等),在本例中我们将使用高斯法:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8aa4e245614f286e0697797a18ba4465_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-41f1d9c941fe239bb40297b998eb6929_l3.png)
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2F_3+F_2}\end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&0&-1&-1 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-02a8a00406479f367627b682099e05c0_l3.png)
因此,获得的步骤系统是:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] -a_3 = -1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-74ed1b18779582d6683ecaa1a9085e3d_l3.png)
我们现在要做的就是澄清未知并发现它的价值。所以从最后一个方程我们发现
![]()
![]()
根据系统的第二个方程,我们计算出
![]()
![]()
![]()
![]()
![]()
最后,从步骤系统的第一个方程,我们找到未知数
![]()
![]()
因此,线性方程组的解为:
![]()
所以向量
![]()
可以用如下的线性组合来表示:
![]()
![]()
![]()
因此,向量之间实际上存在线性相关性。另一方面,如果没有获得方程组的解,则这意味着向量
![]()
它相对于其他向量线性无关,因此,不可能通过线性组合从其他向量获得所述向量。
解决了向量线性组合的练习
练习1
在以下三个向量中,指示哪些对是彼此的线性组合。另外,求出所述向量对的线性组合关系。
![]()
要知道一对向量是否是线性组合,我们必须看看它们的坐标是否成比例。
我们首先检查向量
![]()
与向量
![]()
![]()
其次,我们检查向量
![]()
与向量
![]()
![]()
最后,我们测试向量
![]()
与向量
![]()
![Rendered by QuickLaTeX.com \cfrac{1}{-3} = \cfrac{2}{-6} = \cfrac{-3}{9} = -\cfrac{1}{3} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f818eb5ae0825dd43290331519599c21_l3.png)
所以唯一一对线性组合的向量是
![]()
和
![]()
此外,它们的关系如下:
![]()
或同等学历:
![]()
尽管该语句不要求它,但相互线性依赖的唯一向量是
![]()
和
![]()
因为它们之间存在线性组合。其他对是线性独立的,因为它们不能线性组合。
练习2
求向量之间的线性关系
![]()
和向量集
![]()
和
![]()
![]()
![]()
使得向量
![]()
是其他向量的线性组合,必须满足以下等式:
![]()
因此,我们用每个向量的坐标替换它:
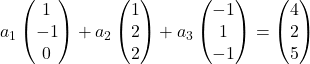
我们将每个向量乘以其常数:
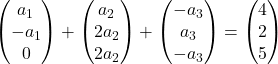
我们添加向量:
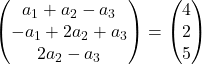
因此我们得到以下方程组:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +a_2-a_3 = 4 \\[2ex] -a_1+2a_2+a_3 =2\\[2ex] 2a_2-a_3 = 5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1ea3ca998fc7d9d9b2cf42d43a5bf0a4_l3.png)
我们用高斯方法求解得到的系统:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c808441bc71bd26e333ebe2169b738ca_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2+F_1}\\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-941792a2de155bc284b14e34dc561418_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3F_3-2F_2} \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&0&-3&3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-7105de2fa579f40818bccc2df48961ab_l3.png)
因此,获得的步骤系统是:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +a_2-a_3 = 4 \\[2ex] 3a_2 =6\\[2ex] -3a_3 = 3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfd5b2d564f66cd225c1a5987241ba14_l3.png)
我们现在要做的就是澄清未知并发现它的价值。所以从最后一个方程我们发现
![]()
![]()
![]()
根据系统的第二个方程,我们计算出
![]()
![]()
![]()
最后,从步骤系统的第一个方程,我们找到未知数
![]()
![]()
![]()
![]()
因此,线性方程组的解为:
![]()
所以向量
![]()
可以用如下的线性组合来表示:
![]()
![]()
![]()
练习3
表达向量
![]()
作为向量的线性组合
![]()
和
![]()
![]()
![]()
我们提出关于向量的线性组合方程
![]()
![]()
因此,我们用每个向量的分量替换它:
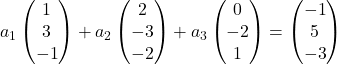
我们将每个向量乘以其各自的未知数:
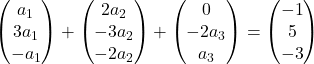
我们进行向量的加法:
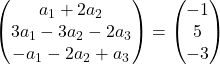
因此我们得到了如下方程组:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +2a_2 = -1 \\[2ex] 3a_1-3a_2-2a_3 =5\\[2ex] -a_1-2a_2+a_3 = -3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-acdcf13a945bca16684be340d27e3523_l3.png)
我们用高斯方法求解得到的系统:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e49ae26fc68a865214bd9b6146b7aa99_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2-3F_1}\\[2ex] \xrightarrow{F_3+F_1} \end{array} \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 0&-9&-2&8\\[2ex] 0&0&1&-4\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e4c56b420242d0abe6f77b3ed1a60e54_l3.png)
因此,获得的步骤系统是:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +2a_2 = -1 \\[2ex] -9a_2-2a_3 =8\\[2ex] a_3 = -4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-03461ed9ebda463d2f0a1bb6894657be_l3.png)
我们现在要做的就是澄清未知并发现它的价值。所以从最后一个方程我们发现
![]()
![]()
从系统的第二个方程,我们找到值
![]()
![]()
![]()
![]()
![]()
![]()
最后,从步骤系统的第一个方程,我们求解未知数
![]()
![]()
因此,线性方程组的解为:
![]()
所以向量
![]()
可以通过线性组合其他向量来表示:
![]()
![]()
![]()
练习4
判断向量是否
![]()
可以表示为向量的线性组合
![]()
和
![]()
在这种情况下,找到连接它们的表达式。
![]()
![]()
使得向量
![]()
是其他向量的线性组合,必须满足以下等式:
![]()
因此,我们用每个向量的坐标替换它:
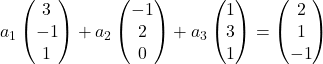
我们将每个向量乘以其系数:
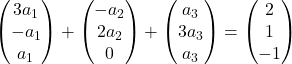
我们添加向量:
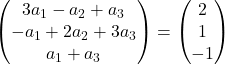
因此,前面的表达式等效于以下方程组:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} 3a_1 -a_2+a_3 = 2 \\[2ex] -a_1+2a_2+3a_3 =1\\[2ex] a_1+a_3 = -1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f51b7e801b8314c51b983f1f24be15e4_l3.png)
我们现在用高斯方法求解得到的系统:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-031b14d5aca6a41d897ca575440b1197_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{3F_2+F_1}\\[2ex] \xrightarrow{3F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2caf1e1104b8b67e13d452bbd20d13b0_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5F_3-F_2} \end{array} \left( \begin{array}{ccc|c}3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&0&0&-30\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d4deec2426c0b9bb0b8e8a3d95155fd9_l3.png)
因此我们得到了如下方程组:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3a_1 -a_2+a_3 = 2 \\[2ex] 5a_2 +10a_3=5\\[2ex] 0 = -30 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e537d5c481ceedeaebf95334d72199ad_l3.png)
然而,最后一个方程永远无法满足,因为无论未知数取什么值,0 永远不会等于 -30。因此,系统无解,这意味着没有线性组合来计算向量
![]()