如何计算向量的模

在此页面上，您将看到矢量大小以及如何使用其公式计算矢量大小的说明。您还可以了解如何从两点找到模块：其起点和终点。此外，您还将了解如何根据向量的模和向量模的属性来确定向量的分量。您甚至可以通过示例、练习和分步问题进行练习。

向量的模是什么？

向量的大小表示其原点和终点之间的距离。因此，矢量的大小等于该矢量的长度。

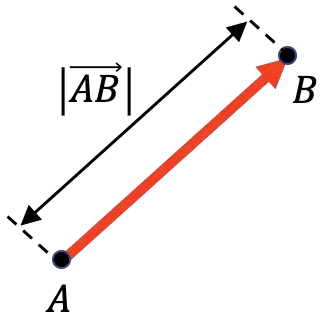
正如您在上面的图形表示中看到的，矢量的大小由矢量两侧的垂直条表示：

$\lvert \vv{AB}\rvert$

另一方面，向量的模与向量的范数相同，所以你也可以看到它是这样写的。这就是为什么有些数学家也用每边两个竖条来表示向量的模：

$\lvert \lvert \vv{AB}\rvert\rvert$

向量模的公式

要找到平面中向量的大小，我们必须应用以下公式：

为了确定向量的大小，我们必须计算其分量平方和的（正）平方根。换句话说，如果我们有以下向量：

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

其模块为：

$\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2}$

例如，我们将使用以下公式计算以下向量的大小：

$\vv{\text{u}} = (4,3)$

$\lvert \vv{\text{u}} \rvert =\sqrt{4^2+3^2} = \sqrt{16+9}=\sqrt{25} = \bm{5}$

用原点和终点的坐标计算向量的大小

我们刚刚看到了当我们知道向量的分量时如何确定向量的大小，但是如果我们只知道它的起点和终点会发生什么？

因此，要根据向量的原点和终点坐标计算向量的大小，必须遵循以下两个步骤：

首先我们找到向量的分量。为此，我们需要减去极值减去原点。
然后我们计算用上一节中看到的公式获得的向量的模。

让我们通过一个例子看看这是如何完成的：

计算以该点为原点的向量的大小
$A(2,1)$

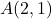
最后一点

$B(-1,4).$

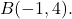
我们首先需要找到向量的分量，因此我们减去它的端点减去它的原点：

$\vv{AB}=B-A=(-1,4)-(2,1)=(-3,3)$

一旦我们知道了向量，我们就可以使用向量幅度公式计算其幅度：

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{(-3)^2+3^2} = \sqrt{9+9}=\sqrt{18}$

我们将结果保留为平方根，因为它不精确。

如何根据向量的模计算向量的分量

我们已经了解了如何从向量的分量中提取向量的大小，但该过程也可以颠倒过来。换句话说，我们可以通过向量的模来计算向量的分量。

从向量的大小找到向量分量的过程称为向量分解。因此，为了分解矢量，我们显然需要它的大小，以及它与横坐标轴（X 轴）形成的角度。

这样向量的 X 和 Y 分量就可以用三角比来计算：

正如您在图像中看到的，矢量的大小与其分量形成直角三角形，因此可以应用三角学的基本公式。

必须考虑到，与向量的模不同，它的分量可以为负，因为正弦和余弦可以取负值。

作为一个例子，我们将求解向量的向量分解，其大小和与 OX 轴的角度为：

$\lvert \vv{\text{u}} \rvert = 10 \qquad \alpha = 60º$

矢量的水平分量等于模乘以角度的余弦：

$\text{u}_x= \lvert \vv{\text{u}}\rvert \cdot \text{cos}(60º)= 10 \cdot 0,5 = 5$

向量的垂直分量等于模乘以角度的正弦：

$\text{u}_y= \lvert \vv{\text{u}}\rvert \cdot \text{sen}(60º)= 10 \cdot 0,87 = 8,7$

所以向量如下：

$\vv{\mathbf{u}}\bm{ = (5 \ ,\ 8,7)}$

向量的模属性

模是一种向量运算，具有以下特征：

向量的大小永远不能为负，它始终等于或大于 0。

$\lvert \vv{\text{u}} \rvert \geq 0$

事实上，唯一存在的幅度为零的向量是零向量，即向量

$\vv{\text{u}}= (0,0) .$

向量与实数（或标量）乘积的大小相当于标量的绝对值乘以向量的大小。因此，以下等式成立：

$\lvert k \cdot \vv{\text{u}} \rvert = \lvert k \rvert \cdot \lvert \vv{\text{u}} \rvert$

三角不等式得到验证：两个向量之和的模分别小于或等于它们各自的模之和。

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert \leq \lvert\vv{\text{u}} \rvert+\lvert\vv{\text{v}} \rvert$

此外，两个向量之和的大小与点积相关，公式如下：

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert = \sqrt{\lvert \vv{\text{u}} \rvert ^2+\lvert \vv{\text{v}} \rvert ^2 +2\cdot \vv{\text{u}}\cdot \vv{\text{v}} \vphantom{\sqrt{x^2}}}$

单位向量

在数学中，单位向量是模等于一的向量。

$\lvert \vv{\text{u}} \rvert=1$

因此，单位向量的长度是一个单位。

让一个向量的模恰好为 1 看起来非常困难，但实际上很容易找到这种类型的向量：

要找到任何向量的单位向量，只需将其除以其模数：

$\vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert}$

金子

$\vv{\text{v}}_u$

是单位向量

$\vv{\text{v}},$

和

$\lvert \vv{\text{v}} \rvert$

你的模块。

单位向量也称为 versor 或归一化向量。

另外，单位向量与原向量具有相同的方向和方向。

例如，我们将计算以下向量的单位向量：

$\vv{\text{v}}=(1,-1)$

为了标准化向量，我们首先需要计算它的大小：

$\lvert \vv{\text{v}} \rvert=\sqrt{1^2+(-1)^2} = \sqrt{2}$

最后，我们通过将原始向量除以其模来计算单位向量：

$\displaystyle \vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert} = \frac{(1,-1)}{\sqrt{2}}= \bm{\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}} \right)}$