添加向量

本页介绍了如何以图形和数字方式在平面中添加两个向量。有 3 种图形添加方法：平行四边形法、头尾相加法和多边形法。此外，您还将找到有关向量加法和向量加法的所有属性的已解决练习。

如何以图形方式添加两个向量？

基本上有两种方法可以从图形表示中添加向量。对于这两种形状，可以获得相同的结果，但有些人喜欢使用头尾法来添加它们，而另一些人则喜欢使用平行四边形方法来添加它们。因此，我们将向您解释这两种方法，以便您选择您喜欢的一种。 😉

另一方面，这两种方法用于将两个向量相加，但是如果我们想要将两个以上的向量相加，会发生什么情况呢？因此，有必要使用多边形方法，该方法包括依次使用平行四边形方法。您还可以在头尾法和平行四边形法之后找到它的解释。

平行四边形方法或规则

平行四边形规则或平行四边形方法（或平行四边形定律）是一种图形程序，可让您以非常简单的方式找到两个向量的总和。应用此流程的步骤如下：

1. 首先，我们绘制向量并将它们放置在同一应用点，也就是说，我们将两个向量的原点放在同一点。
2. 然后我们在一个向量的末端画一条与另一个向量平行的线。我们用另一个向量重复该步骤。因此，我们将得到平行四边形的图（该规则的名称由此而来）。
3. 最后，求和的结果将是从公共原点到两条平行线相交点的向量。

看下面的通用示例，其中两个向量按照平行四边形规则相加：

矢量之和的结果是它们与其平行线形成的平行四边形的对角线。

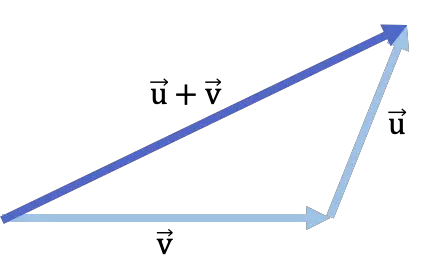
头尾法

头尾法，也称为三角形法，是另一种可以图形方式添加两个向量的过程。在这种情况下，要遵循的步骤是：

1. 移动添加的向量并将其放置，使其原点位于另一个添加的向量的末尾。
2. 向量相加的结果是从第一个相加向量的开头到另一个向量的结尾的段。如果仔细观察，就会发现两个向量相加，向量相加就形成了一个三角形。

下面是使用头尾法进行向量加法的示例：

多边形法

一旦我们了解了如何以图形方式求解两个向量的和，我们就会看到当我们有两个以上向量时它是如何完成的。

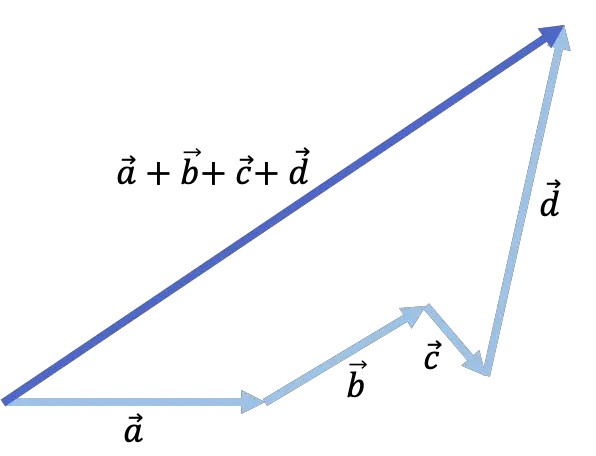
当您想要将三个或更多向量相加时，有一种技术可以加快运算的计算速度。该技术称为多边形方法，由连续应用头尾方法组成：

1. 我们首先需要将每个向量放在另一个向量之后，以便一个向量的原点与另一个向量的末端重合。我们放置它们的顺序并不重要。
2. 和的结果是将第一个向量的开头与最后一个向量的结尾相连接而获得的向量。

看下面的例子，其中添加了 4 个向量：

以数值方式计算两个向量的总和

一旦我们知道如何以几何方式将向量相加，我们将了解如何以数值或代数方式计算向量和。

例如，向量之间的和

和

东方：

另一方面，我们必须记住，两个向量的向量加法与向量的模的加法不同，实际上结果是完全不同的。您可以在矢量幅度（也称为矢量幅度）的属性中看到这两种运算之间的差异。

添加矢量属性

向量加法具有以下特点：

• 关联性：在多个向量之和之间放置括号不会修改运算结果。

• 交换律——与向量减法不同，两个向量之间的加法结果与它们相加的顺序无关。

• 相反元素的性质：向量加上它的相反元素（即它的负数）之和等于0。

• 中性元素的性质：显然，任何向量加上零或零向量都等价于向量本身：

解决了向量加法问题

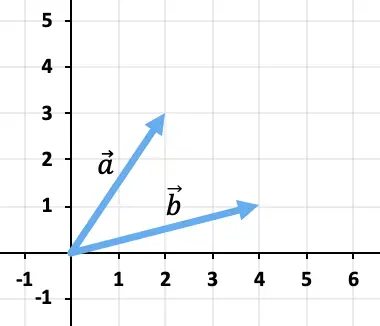
练习1

以图形方式计算向量之和

和

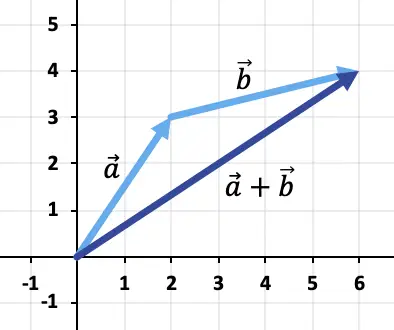
为了将两个向量相加，我们将使用头尾规则。因此，我们将向量的原点放在

在向量的末尾

，总和将是从坐标原点到坐标末尾的向量

因此，向量相加的结果为：

练习2

以图形方式求解向量之和

和

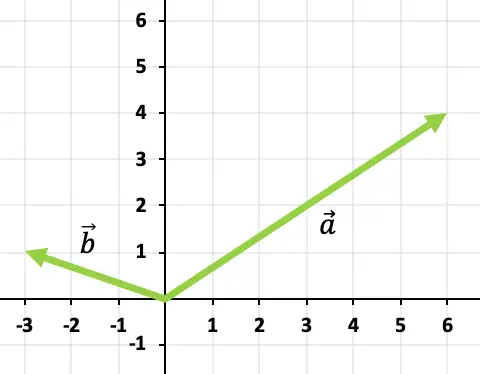
为了将两个向量相加，我们将使用头尾规则。因此我们将找到向量的原点

在向量的末尾

，和向量将是从轴的原点到轴的末尾的向量

因此，向量相加的结果为：

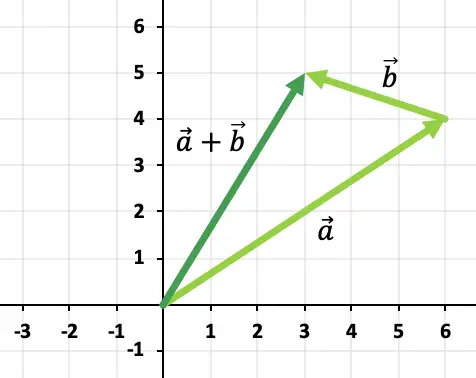
练习3

以图形方式确定图中表示的所有向量相加所得的向量：

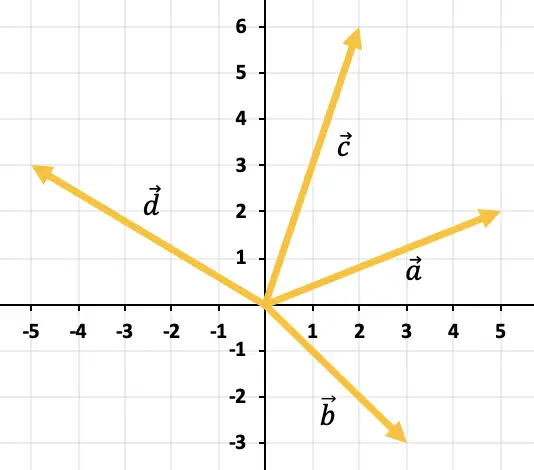
要从图中添加 2 个以上向量，必须使用多边形规则。因此，我们必须移动向量，使它们保持连续，也就是说一个接一个（顺序无关）。因此，所有向量的总和将是从第一个向量的原点到最后一个向量的末尾的向量。

所以4个向量相加的结果就是红色表示的向量：

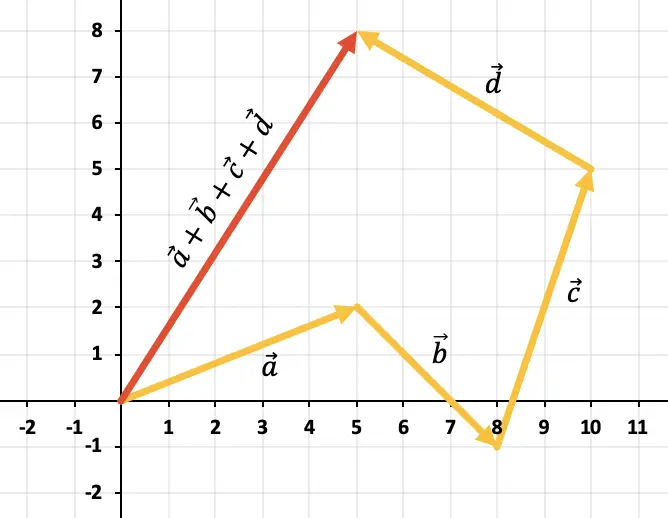
练习4

求以下向量的数值总和：

要对两个向量进行数值相加，必须将它们各自的坐标相加：

练习5

分析计算以下向量的总和：

要对向量进行数值加法，您必须将它们各自的坐标相加：