反埃尔米特（或反埃尔米特）矩阵

在此页面上，您将了解什么是反埃尔米特矩阵，也称为反埃尔米特矩阵。您将找到反厄米矩阵的示例、它们的所有属性以及此类复数方阵的形状。最后，您将找到如何将任何复杂矩阵分解为反厄米特矩阵与另一个厄米特矩阵之和的解释。

什么是反埃尔米特矩阵？

出于好奇，这种矩阵之所以如此命名，是因为它满足埃尔米特矩阵的相反条件，埃尔米特矩阵的名字来源于法国重要数学家查尔斯·埃尔米特，他是一位 19 世纪的数学教授和研究员，他做出了重要的研究，包括线性代数领域。

反厄米矩阵的示例

一旦我们了解了反埃尔米特矩阵（或反埃尔米特矩阵）的定义，我们就会看到一些不同维度的反埃尔米特矩阵的例子：

2×2 阶反埃尔米特矩阵的示例

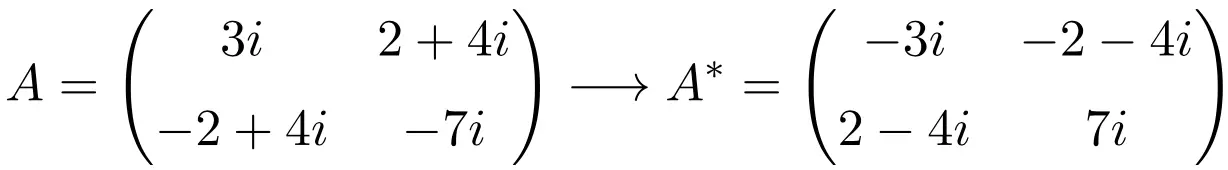
维度为 3×3 的反埃尔米特矩阵示例

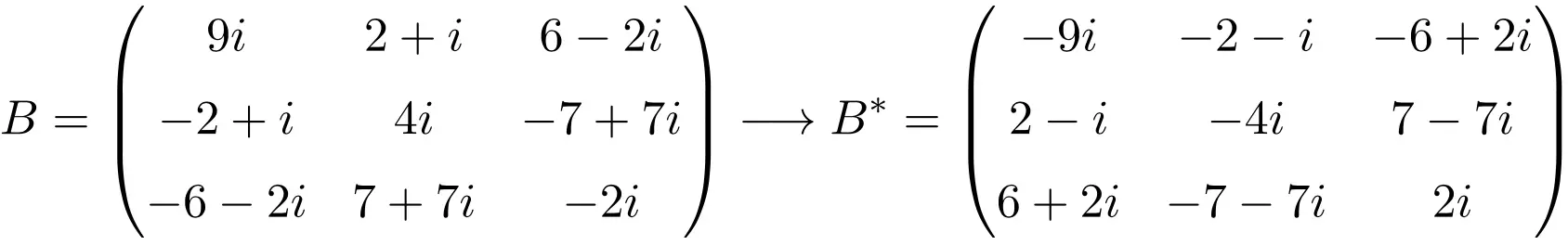
大小为 4×4 的反埃尔米特矩阵示例

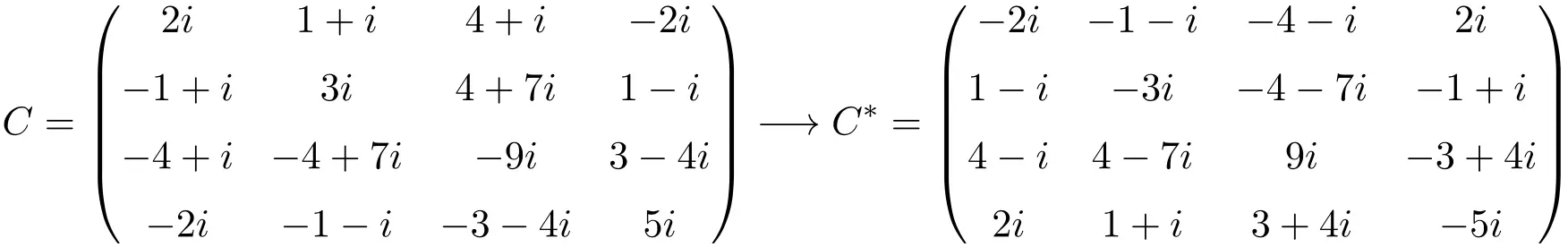
正如您所看到的，矩阵 A、B 和 C 是反埃尔米特矩阵，因为每个矩阵的共轭转置矩阵等于矩阵本身，但所有元素都改变了符号。

反厄米矩阵的结构

如果您已经看过前面的示例，反埃尔米特矩阵始终具有相同的结构：它们由主对角线上的虚数（没有实部）以及位于第 i 行和第 j 行的复数元素组成线。列必须与第 j 行第 i 列的元素具有相同的虚部和相同的实部，但符号不同。

虽然这看起来有点复杂，但通过以下示例肯定可以更好地理解：

2×2 维反埃尔米特矩阵的结构

如您所见，反埃尔米特矩阵的主对角线的元素完全是虚数，次对角线的元素具有相同的虚部，而实部的符号发生了变化。

因此，反埃尔米特矩阵的实部必须是反对称的，虚部是对称的。

反厄米矩阵的性质

现在我们来看看这种类型的复数方阵有什么性质：

• 每个反埃尔米特矩阵都是正规矩阵的一个例子。尽管并非所有正规矩阵都是反隐矩阵。

• 任何反厄米矩阵都是可对角化的。此外，生成的对角矩阵仅包含纯虚数元素。

• 因此，反埃尔米特矩阵的特征值（或特征值）始终是虚数。

• 同样，反埃尔米特矩阵的不同特征值的特征向量（或特征向量）是正交的。

• 实数矩阵，也就是说没有元素具有虚部，当且仅当它是反对称矩阵 时，它是反埃尔米特矩阵。

• 反埃尔米特矩阵可以表示为实反对称矩阵与虚对称矩阵之和。

• 两个反厄米特矩阵的和（或减法）等于另一个反厄米特矩阵。

• 如果标量是实数，则反埃尔米特矩阵和标量的乘积的结果是另一个反埃尔米特矩阵。

• 如果指数为奇数，则反埃尔米特矩阵的幂等于反埃尔米特矩阵；另一方面，如果它被提高到偶数指数，则结果将是埃尔米特矩阵。

• 是的

  

  是反埃尔米特矩阵，那么乘积

  

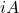
  是埃尔米特矩阵。

将复矩阵分解为反埃尔米特矩阵和埃尔米特矩阵

任何包含复数的矩阵都可以分解为一个反埃尔米特矩阵与另一个埃尔米特矩阵之和。但为此，您需要了解这些类型矩阵的以下特征：

• 复数方阵加上其转置共轭之和相当于 Hermitian（或 Hermitian）矩阵：

• 复数方阵与其转置共轭之差等于反埃尔米特矩阵：

• 因此，所有复矩阵都可以分解为埃尔米特矩阵和反埃尔米特矩阵之和。该定理称为Teoplitz 分解：

其中C是我们要分解的复矩阵，C*是它的转置共轭，最后A和B分别是矩阵C分解成的厄米矩阵和反厄米矩阵。