在这里您将找到什么是函数双曲正切的导数。此外,您将能够看到双曲正切导数的几个已解决的示例。最后,我们向您展示双曲正切导数的公式。
双曲正切的导数公式
x 的双曲正切的导数等于 1 除以 x 的双曲余弦的平方。 x的正切的导数也相当于x的双曲正割的平方,1减去x的双曲正切的平方。
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tanh}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=\text{sech}^2(x)=1-\text{tanh}^2(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a7c392afdb3bbf504e167e15fb2fee6_l3.png)
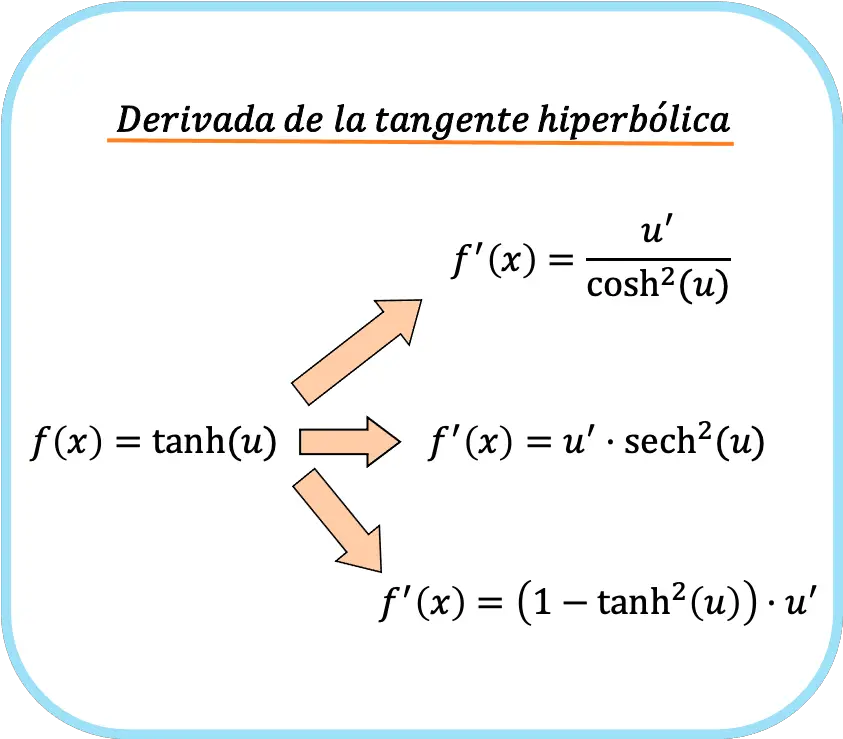
另一方面,如果在函数参数中我们有一个 x 以外的函数,我们必须应用链式法则。那么双曲正切导数的三个公式是:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tanh}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cosh}^2(u)}=\text{sech}^2(u)\cdot u'=\left(1-\text{tanh}^2(u)\right)\cdot u'\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5ee01c6675067b20f71ea8ac4efcfe5_l3.png)
这并不意味着每次推导双曲正切时都必须使用所有三个公式,而是我们可以使用其中任何一个公式来推导它。因此,根据双曲正切参数的函数,最好使用一种或另一种公式。下面是几个示例,您可以在其中了解如何导出函数的双曲正切。
双曲正切的导数与正切的导数几乎相同,但有一个小细节使它们完全不同。您可以在以下链接中看到有什么区别:
➤参见:正切导数公式
双曲正切导数的例子
了解了双曲正切的导数公式是什么之后,这里有几个此类三角函数的导数的求解示例,以便您充分了解如何推导双曲正切。
示例 1:2x 双曲正切的导数
![]()
为了导出本例中的双曲正切,我们将使用双曲余弦公式,当然您也可以使用您喜欢的任何公式。
![]()
我们知道2x的导数是2,所以整个函数的导数是:
![]()
示例 2:x 平方的双曲正切的导数
![]()
函数双曲正切的导数规则为:
![]()
一方面,我们将函数与参数 x 2微分,得到 2x,然后我们使用以下公式求解整个函数的导数:
![]()
示例 3:双曲正切立方的导数
![]()
在这种情况下,我们必须导出函数的双曲正切,而且还要求其幂。所以我们需要使用势函数的导数公式、双曲正切导数规则和链式法则:
![]()
正切导数的证明
在本节中,我们将演示双曲正切导数的公式。为此,我们将从连接三个双曲三角比率的三角恒等式开始:
![]()
➤注意:要理解证明,你需要知道什么是双曲正弦的导数,什么是双曲余弦的导数。因此,我们建议您在继续之前访问链接的页面。
现在,我们应用商的导数公式:
![]()
![]()
![]()
我们使用以下公式简化分数分子的表达式:
![]()
![]()
正如您所看到的,前面的等式对应于双曲正切导数的第一个公式。同样,双曲正割是双曲余弦的乘法逆元,因此也推导出第二个公式:
![]()
最后,我们可以通过将上一步的分数转化为分数减法,得到双曲正切导数的第三条规则:
![]()
![]()
![]()