双曲余弦函数

4 7 月, 2023

在这里您将找到有关双曲余弦函数的所有内容：它的公式是什么、它的图形表示、它的特征、与其他函数的数学关系等等。

双曲余弦公式

双曲余弦函数是主要的双曲函数之一，用符号cosh(x)表示。双曲余弦等于 e ^x加上 e ^-x之和除以 2。

因此，双曲余弦的公式为：

$\displaystyle\text{cosh}(x)=\cfrac{e^{x}+e^{-x}}{2}$

因此，双曲余弦在数学上与指数函数相关。在以下链接中您可以看到此类函数的属性：

➤请参阅：指数函数的性质

双曲余弦的图形表示

双曲余弦函数的图形表示形式为二次函数（或抛物线）：

双曲余弦

➤请参阅：二次函数的图形表示。

在此图中，我们可以清楚地看到双曲余弦是偶函数，因为它关于 y 轴对称。

另一方面，双曲余弦的图形与作为周期函数的余弦（三角函数）的图形有很大不同。您可以在以下链接中查看余弦的图形表示以及与双曲余弦的所有差异：

➤请参阅：余弦函数的图形表示

双曲余弦的特征

双曲余弦遵循以下属性：

双曲余弦函数的定义域都是实数：

$\text{Dom } f = \mathbb{R}$

相反，双曲余弦函数的范围（或范围）为 1 并且所有数字都大于 1：

$\text{Im } f= [1,+\infty)$

双曲余弦是连续且偶函数。

$\displaystyle \text{cosh}(-x)=\text{cosh}(x)$

该函数与 Y 轴相交于点 x=0。

$(0,1)$

另一方面，该函数与 X 轴没有交点。

双曲余弦函数的无穷大的两个极限（正和负）给出正无穷大。

$\displaystyle\lim_{x\to+\infty}\text{cosh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{cosh}(x)=+\infty$

双曲余弦一直减小，直到 x = 0，从那时起它无限增加，因此该函数在 x = 0 处具有最小值。

$(0,1)$

该函数在其整个定义域内都是凸函数，因此没有拐点。

双曲余弦函数的导数是双曲正弦：

$f(x)=\text{cosh}(x) \ \longrightarrow \ f'(x)=\text{senh}(x)$

双曲余弦函数的积分就是双曲正弦：

$\displaystyle \int \text{cosh}(x) \ dx= \text{senh}(x) + C$

双曲余弦函数的泰勒多项式（或麦克劳林级数）如下：

$\displaystyle\text{cosh}(x)=1+\cfrac{x^2}{2!}+\cfrac{x^4}{4!}+\cfrac{x^6}{6!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n}}{(2n)!}$

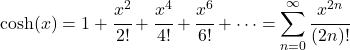
双曲余弦函数的拉普拉斯变换如下：

$\mathcal{L}\bigl[\text{cosh}(at)\bigr]=\cfrac{s}{s^2-a^2}$

双曲余弦的数学关系

接下来，我们将了解如何从其他双曲函数计算双曲余弦，因为它们在数学上都是相关的。

基本方程将双曲余弦与双曲正弦联系起来：

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

➤请参阅：双曲正弦

三个主要双曲函数（双曲正弦、双曲余弦和双曲正切）可以通过以下等式关联：

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

另一方面，两个不同数字相加（或相减）的双曲余弦可以通过以下公式确定：

$\text{cosh}(x+y)=\text{cosh}(x)\text{cosh}(y)+\text{senh}(y)\text{senh}(x)$

$\text{cosh}(x-y)=\text{cosh}(x)\text{cosh}(y)-\text{senh}(y)\text{senh}(x)$

一个数的两倍的双曲余弦等于该数的双曲余弦和双曲正弦的平方和：

$\text{cosh}(2x)=\text{cosh}^2(x)+\text{senh}^2(x)$

两个双曲余弦的加法或减法可以通过应用以下公式来计算：

$\displaystyle\text{cosh}(x)+\text{cosh}(y)=2\text{cosh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{cosh}(x)-\text{cosh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{senh}\left(\frac{x-y}{2}\right)$

最后，双曲余弦的平方可以通过以下公式计算：

$\text{cosh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)+1\Bigr)$

发表评论取消回复