双曲余割弧导数

在本文中，我们将解释如何导出函数的双曲反余割。您还可以找到双曲反余割导数的工作示例。

双曲余割弧的导数公式

x 的反双曲余割的导数等于负 1 除以 x 乘以一加 x 平方根的乘积。

因此，函数的反双曲余割的导数是减去该函数的导数除以该函数乘以一的根加上函数平方的乘积。

综上所述，双曲反余割函数导数的计算公式为：

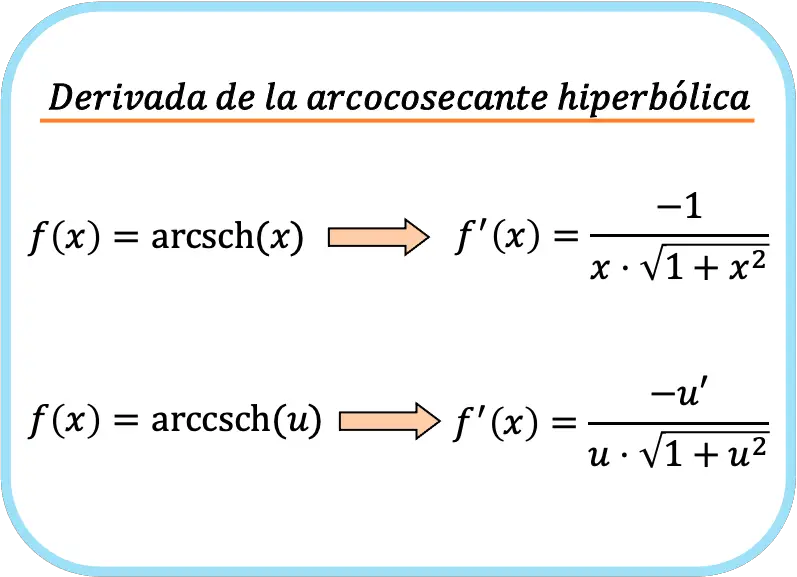
虽然我们提出了两个公式，但这并不意味着它们是不同的。如果仔细观察，第二个公式与第一个公式类似，但应用了链式法则。

双曲余割弧的导数示例

给定双曲反正余割导数的公式，我们将导出两个这样的函数，以便您了解它是如何完成的。

实施例1

在本练习中，我们必须使用链式法则求反双曲余割的导数公式，因为在参数中存在一个与 x 不同的函数：

因此，为了求导数，我们需要将 u 替换为 3x，将 u’ 替换为其导数，即 3：

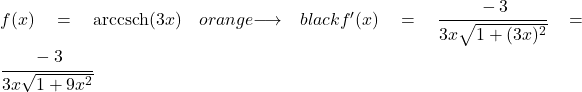
实施例2

在这种情况下，我们的双曲反余割参数中有一个多项式函数，因此我们还需要使用链式法则来推导它：

因此，我们将参数函数的导数放入分数的分子中，并在分母中通过多项式函数改变 u：

类似商品

• 双曲反余弦的导数
• 双曲余割的导数
• 双曲余弦的导数
• 余割弧的导数
• 由余割导出
• 反余弦的导数
• 余弦的导数