单项式运算

在此页面上，我们解释如何使用单项式执行所有运算（加法、减法、乘法、除法和幂）。此外，您将能够看到每种类型的单项式运算的示例，并通过逐步解决的练习进行练习。

单项式的加法和减法

两个或多个单项式只有在相似单项式时才能进行加或减，即两个单项式具有相同的文字部分（相同的字母和相同的指数）。

那么，两个相似单项式的和（或减法）等于由相同文字部分组成的另一个单项式与这两个单项式的系数之和（或减法）。

单项式的加法和减法也分别称为单项式的加法和减法。

单项式的加法和减法示例

为了让您能够清楚地了解如何对两个或多个单项式进行加法和减法，我们在下面提供了几个示例：

• 

• 

• 

• 

• 

最后一个示例中的单项式无法相加或相减，因为它们不相似，或者换句话说，它们具有不同的未知数或指数。

单项式多次乘积

要求解单项式与数字的乘积，只需将单项式的系数乘以该数字，而单项式的文字部分保持不变。

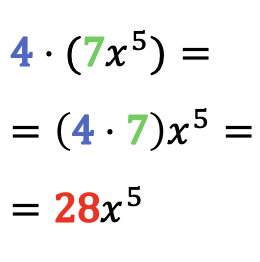
数字乘以单项式的示例

• 

• 

• 

• 

单项式的乘法

两个单项式相乘的结果是另一个单项式，其系数是单项式系数的乘积，其字面部分是通过将具有相同基数的变量相乘（即通过将它们的指数相加）获得的。

因此，要乘两个不同的单项式，我们必须将它们之间的系数相乘，并将具有相同底数的幂的指数相加。

然而，如果我们将两个具有不同基幂的单项式相乘，我们只需将它们的系数相乘并保持幂相同。例如：

另一方面，当单项式相乘时，必须考虑符号规则：

• 正单项式乘以一个正单项式得到另一个正单项式。
• 正单项式乘以负单项式（反之亦然）等于负单项式。
• 两个负单项式相乘得到一个正单项式。

单项式乘法的例子

以下是单项式之间乘法的几个示例，您可以了解它是如何完成的：

• 

• 

• 

• 

• 

正如您所看到的，求解单项式乘法相对简单。但你应该记住，单项式也可以与多项式相乘，甚至两个或多个多项式也可以相乘。如果您更感兴趣，您可以通过单击多项式乘法来了解所有这些运算的工作原理。

单项式除法

在数学中，单项式除法的结果是另一个单项式，其系数等于单项式系数的商，其字面部分是通过将具有相同基数的变量相除（即减去它们的指数）获得的。

显然，任何单项式的除法也可以表示为分数：

与乘法一样，单项式除法也需要应用符号定律：

• 正单项式除以一个正单项式得到另一个正单项式。
• 正单项式除以负单项式（反之亦然）相当于负单项式。
• 两个负单项式相除得到一个正单项式。

单项式除法的例子

您可以在下面看到有关如何划分两个或多个单项式的更多示例：

• 

• 

• 

• 

• 

当然，在某些时候，当你学到数学新知识时，你会问自己：它的用途是什么？嗯，单项式除法用于除多项式。事实上，由于两个单项式被错误地除法而导致多项式除法错误是很常见的。这就是为什么我们建议，既然您已经熟悉了单项式之间的除法，那么您就可以了解如何计算多项式除法，因为现在您学习该过程会更容易（它相当复杂）。

单项式的幂

在数学中，为了计算单项式的幂，单项式的每个元素都会被提升到幂的指数。换句话说，单项式的幂包括将其系数及其变量（字母）提高到幂的指数。

请记住，根据幂的性质，当两者都提高已经很高的项时，指数会相乘。这就是为什么对于单项式的幂，每个字母的指数总是乘以表示幂的指数。

另一方面，要正确执行此操作，您必须记住以下幂属性：

• 负单项式升到偶数指数相当于正单项式。
• 相反，负单项式提升到奇数指数会产生负单项式。

单项式幂的示例

我们给您提供一些示例，以便您可以清楚地了解单项式幂的计算方式：

• 

• 

• 

• 

• 

与单项式相结合的运算

一旦您了解了单项式的所有运算是什么，就会知道它们也可以相互组合。也就是说，我们可以找到要求我们解决涉及所有类型的单项式运算的练习：加法、减法、乘法、除法和幂。

但别担心，它们并不像看起来那么困难。您唯一需要记住的是组合操作的解析顺序：

1. 首先，解决括号内单项式的运算。
2. 然后计算单项式的幂。
3. 第三，进行单项式的乘法和除法。
4. 最后，确定单项式的加法和减法。

我相信通过解决一个例子你会更清楚地看到它：

单项式组合运算示例

首先，我们必须求解括号内单项式的运算：

在这种情况下，我们没有权力。现在让我们计算单项式的乘法和除法：

最后，我们添加和减去单项式：

解决了单项式运算的练习

如果您想练习，我们在下面给您留下几个练习，逐步解决单项式运算的 ESO 难度。

练习1

计算以下单项式的加法和减法：

练习2

求解以下单项式乘法：