分数或带分数是表示一个量除以另一个量的数值表达式。因此,它是由两个数字的商表示的值。使用这种类型的数字,我们可以表示小数和整数,甚至可以表示比例。接下来,我们将以更数学的方式定义分数,并向您展示一些示例,以便您以图形方式理解这个概念。
什么是分数?
分数等于我们从一个单位中分成相等部分的部分数。因此,从图形上看,它由中间由一条水平线分隔的两个术语表示。更准确地说,我们在线的顶部找到分子,分母下方。
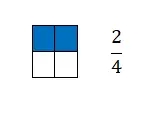
正如您所看到的,分数是一个非常容易绘制图表的数学概念,因为它们与比例密切相关。这就是为什么在前面的示例中我们用小数表示彩色方块的数量。
分数项
分数的两部分是:
- 分子:这项位于水平线上方,这是我们写下我们取出的件数的地方。我们可以找到正分子、负分子和零(等于零)分子。
- 分母:另一项位于该线下方,这是我们写下该单位分为的部分总数的地方。我们可以找到正分母和负分母,但它们不能为零。
分数类型
分数有很多种,具体取决于组成它们的数字以及它们与其他分数的等价性。接下来,我们将定义所有存在的类别,并评论使它们与其他类别区分开来的特征:
- 真分数:分子小于分母的分数。如果将这些分数转换为小数,您将得到一个介于 0 和 1 之间的数字。它不能大于一,因为分子的值始终小于分母的值,因此不会超过单位。
- 假分数:分子大于分母的分数,在这种情况下,它们表示大于单位的数值。例如,8/5 等于 1.6,大于 1。这是表示带分数的另一种方式,如下所示。
- 带分数:也称为带分数,是由整数和带分数组成的分数。基本上它们用分数前面的整数值表示,因此要将它们转换为假分数,您需要将整数部分乘以分母,然后将其添加到分子并保持分母相同。
- 小数分数:分母表示等于 10 的幂的数量,例如:6/10、34/1000 或 5/100。它们用于十进制表示法,在将精确的十进制数转换为带分数时最常见。我们将在下一节中更详细地讨论这一点。
- 复合分数:是由分子或分母或两者都由另一个分数组成的分数。因此,为了简化这些表达式并将它们显示为单个分数,我们需要将分子除以分母。一旦我们解释了分数之间的除法,这一点就会变得更清楚。
- 等值分数:是指那些等价于相同数字的分数,尽管它们不由相同的分子或分母组成。例如,8/4 = 4/2 = 2,两个分数都等于 2。在这种具体情况下,因为第一个分数等于第二个分数的两倍,因此,它保持比例关系。
- 不可约分数:这些分数无法进一步简化,因为分子和分母没有公因数,因此不能被任何数字整除。这种类型的一些示例包括:9/5、5/6、7/8 等。要知道如何检测它们,了解如何计算最大公约数非常重要。
分数运算
现在我们知道了存在的不同类别的分数,我们将了解如何使用带分数来解决不同的算术运算。应该注意的是,这比整数运算稍微复杂一些,尽管一旦您理解了方法,一切就很容易了。此外,我们不仅会解释理论,还会向您展示一些示例。话虽如此,让我们开始吧。
分数和
具有公分母的分数相加非常简单,因为您只需将两个分子相加并保持分母相同。另一方面,将不同分母的分数相加会有点棘手,因为您必须找到分母的最小公倍数。然后,我们必须通过将 lcm(新分母)除以旧分母来添加每个分子的乘积。为了更好地理解,您可以看下图:
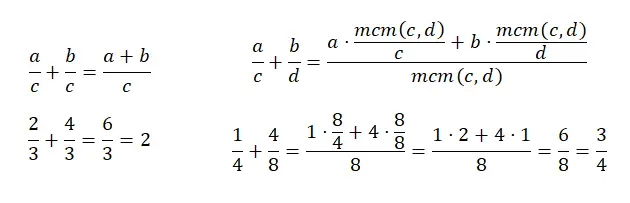
减法分数
具有公分母的分数的减法与加法非常相似,事实上,除了分子之和之外,所有操作都以相同的方式完成,因为您必须做减法而不是加法。在不同分母的分数减法中,会发生同样的事情,实际上是同一件事,除了我们必须减去 ,而不是通过将 lcm 除以旧分母来添加分子的乘积。这是另一个图表:
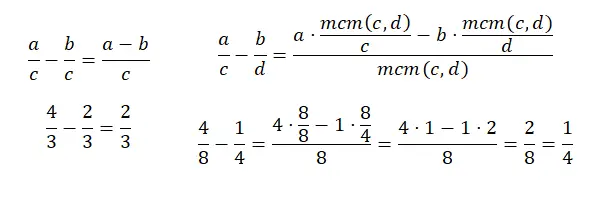
分数乘法
无论分母是否相同,分数乘法都可以用同样的方法解决。基本上,您必须将分子乘以一部分,将分母乘以另一部分。这可能是最简单的运算,因为您只需要执行两次乘法。
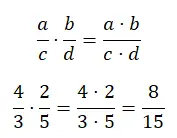
分数除法
除以分数也很容易解决,只需将叉号相乘即可。换句话说,分子是第一个分数的分子乘以第二个分数的分母的结果。而分母是第一个分数的分母和第二个分数的分子的乘积。
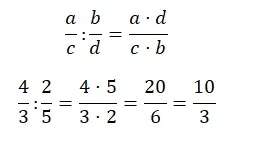
化简分数
简化分数或约简分数本身并不是算术运算,但了解如何执行它非常重要,而且我们已经对分数类型进行了一些介绍。因此,为了简化带分数,我们需要将分子和分母除以相同的数字。一般来说,我们会选择最大公因数来进行这种简化。在下图中您可以找到一个示例。
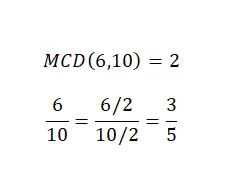
正如您所看到的,我们有两个等价的分数,因此两者都代表相同的数值,但第二个比第一个更简单。因此,我们成功地实现了简化的目标。
如何将小数转为分数,反之亦然?
生成分数是从小数(精确小数或重复小数)获得的不可约分数。当然,我们需要根据小数类型使用不同的方法,我们将在下面讨论。
从精确小数转换为生成分数
在这种情况下,我们可以求助于我们在开头评论过的小数部分。简单来说,我们需要在分子中写入数值,但不带小数点。在分母中,我们写下十的幂,它的零个数与分子中的数字个数一样多。
但是,如果我们有一个大于 1 的小数,例如 4.25,那么我们需要将我们拥有的完整单位数乘以分母值,并将其添加到原始分子。下面您将找到每种类型的示例:
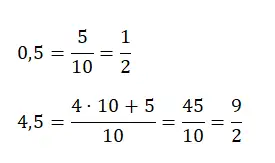
将纯循环小数转换为生成分数
当我们有一个纯周期小数时,如果我们想得到生成分数,我们必须将相同的值放入分子中,但不带小数点,然后减去整数部分。虽然分母等于仅由 9 组成的数字,但我们必须专门写出与原始数字的小数部分中的位数一样多的 9。这个系统有点令人困惑,但通过几个例子,我们就会明白:
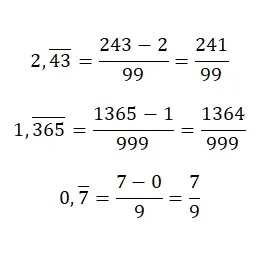
将混合重复小数转换为生成分数
如果有混合重复的十进制数,我们将不得不应用相当复杂的规则。首先,我们将在分子中写出不带逗号的数字,然后减去整数部分,后跟非循环小数,也不带逗号。至于分母,您需要写出与周期性小数部分中的数字一样多的 9,然后写与非循环小数部分中的数字一样多的零。
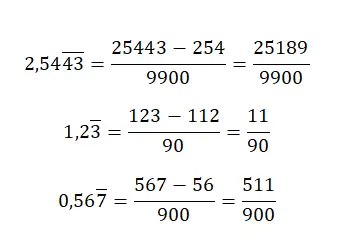
将分数转换为小数
要从分数变为小数,只需将分子除以分母,因为带分数只不过是两个值之间的商。因此,通过解决除法,您可以得到相应的十进制数。在下图中,您可以找到一些相当简单的示例:
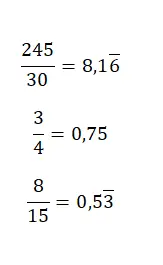
分数练习
现在您已经了解了分数的所有理论,我们建议您做一些练习。通过这种方式,您将更深入地学习所有概念,并且在考试当天,您将更快地解决计算问题。此外,您将看到现有的所有类型的分数练习,并且您将知道如何相应地解决它们。最后,让我告诉您,我们还为您提供了一个在线分数计算器,您可以用它来解决所有分数运算。