在本文中,我们将了解如何在图形上表示任何类型的函数。此外,您还将找到有关在图表上表示函数的已解决的分步练习。
如何在图上表示函数
要在图形上表示函数,必须执行以下步骤:
- 求函数的定义域。
- 使用笛卡尔轴计算函数的截止点。
- 计算函数的渐近线。
- 研究函数的单调性并找出其相对极值。
- 研究函数的曲率并找到其拐点。
- 绘制截止点、渐近线、相对极值和拐点,然后绘制函数。
表示函数的示例
为了让您能够看到函数是如何以图形方式表示的,我们将逐步解决以下练习:
- 在图上绘制以下有理函数:
![]()
首先要做的是计算函数的定义域。这是一个有理函数,因此我们需要将分母设置为零,以查看哪些数字不属于函数的定义域:
![]()
![]()
因此,当 x 为 1 时,分母将为 0,因此该函数将不存在。因此,函数的域由除 x=1 之外的所有实数组成。
![]()
为了找到与 X 轴的交点,我们必须求解方程
![]()
由于该函数在 X 轴上的值始终为 0:
![]()
![]()
期限
![]()
这涉及到将整个左侧除,因此我们可以将其乘以整个右侧:
![]()
![]()
![]()
因此与 OX 轴的交点为:
![]()
为了找到与 Y 轴的交点,我们计算
![]()
因为 x 在 Y 轴上始终为 0:
![]()
因此,与OY轴的分界点为:
![]()
在这种情况下,当函数通过坐标原点时,与X轴的交点与与Y轴的交点重合。
一旦我们知道了域和截止点,我们就需要计算函数 的渐近线。
要查看函数是否具有垂直渐近线,我们需要计算函数在不属于定义域的点处的极限(在本例中 x=1)。如果结果是无穷大,则它是垂直渐近线。然而:
![]()
由于当 x 趋于 1 时函数的极限给出无穷大,因此 x=1 是垂直渐近线:
一旦计算出垂直渐近线,就需要计算函数相对于它的横向极限。因为我们不知道函数从左侧接近 x=1 时是否会趋于 -∞ 还是 +∞,并且我们也不知道函数何时从右侧接近 x=1。
因此,我们继续计算函数在 x=1 处的左侧极限:
![]()
为了数值计算某个点的横向边界,我们必须将一个数字代入非常接近该点的函数中。在本例中,我们希望左侧有一个非常接近 1 的数字,例如 0.9。因此,我们将点 0.9 代入函数中:
![]()
渐近线的横向极限只能给出+∞或-∞。由于将左侧非常接近 1 的数字代入函数中,我们得到了负结果,因此左侧的极限为 -∞:
![]()
现在我们对右侧边界执行相同的过程:
![]()
我们将右边一个非常接近 1 的数字代入函数中。例如第1.1点:
![]()
在这种情况下,侧极限结果是正数。因此右边的极限是+∞:
![]()
总之,当 x=1 时,函数趋向于左边为负无穷大,右边为正无穷大:
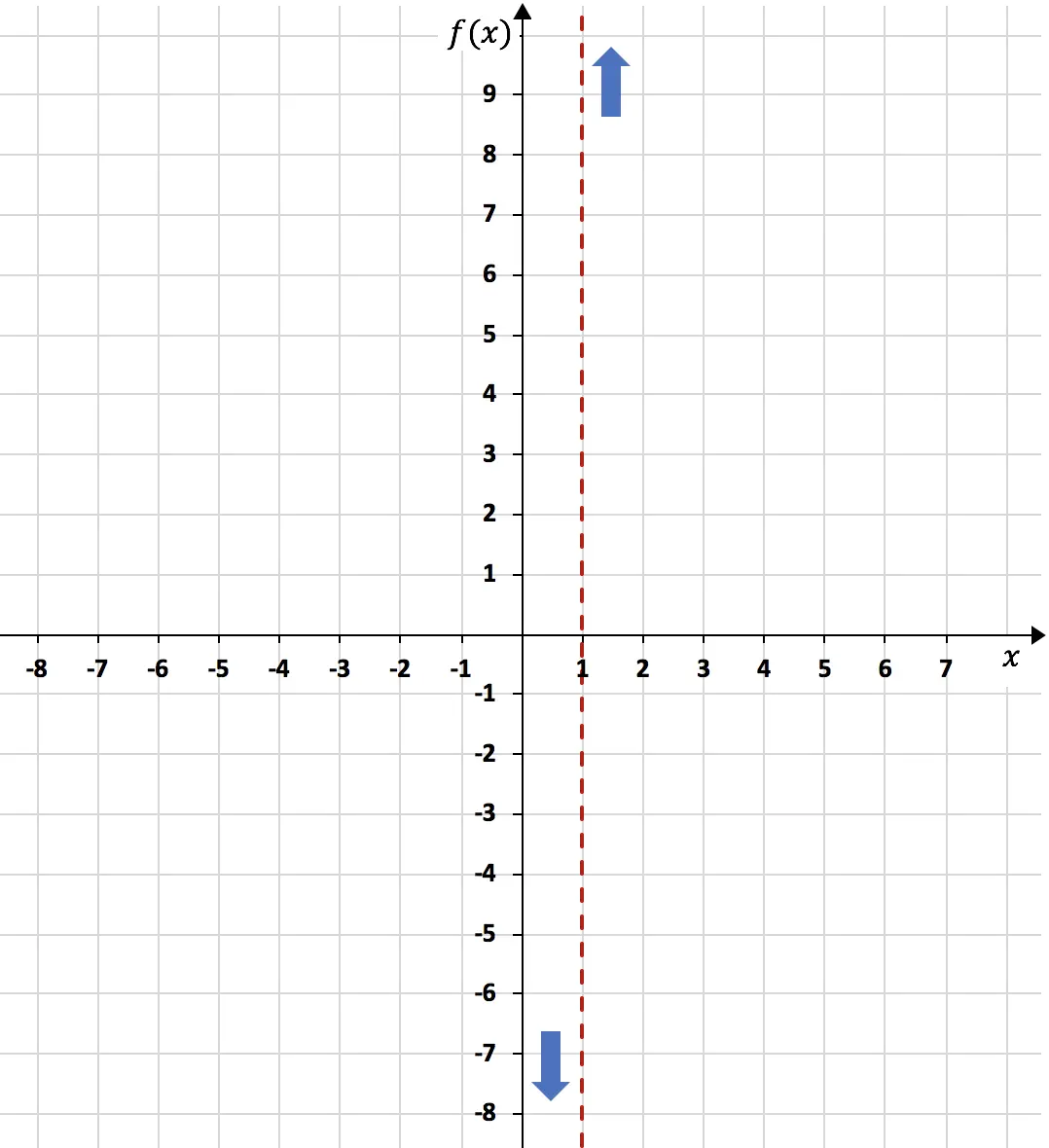
另一方面,函数的水平渐近线将是函数无限极限的结果。然而:
![]()
记住如何计算有理函数的无限极限:
![\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”></p>
</p>
</div>
<p>函数的无限极限给了我们+∞,因此函数没有水平渐近线。</p>
<p>我们现在计算斜渐近线。斜渐近线的形式为</p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c969e4b99985b44006e57d554ff0247_l3.png)
![]()
。和
![]()
其计算公式如下:
![]()
![]()
x 就好像它有 1 作为分母:
![]()
这是分数除法,所以我们将它们横向相乘:
![]()
![]()
我们计算极限:
![]()
所以m=1。现在我们计算
![]()
具有以下公式:
![]()
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-1x\right] = \cfrac{+\infty}{+\infty} -(+\infty) = +\infty - \infty](https://mathority.org/wp-content/ql-cache/quicklatex.com-10dfa8fdcfbf0c978e02374654a66b7d_l3.png)
但是我们得到了不确定性无穷大减去无穷大,所以我们必须将这些项减少到一个公分母。为此,我们将 x 项乘以并除以分数的分母:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty}\left[\cfrac{x^2}{x-1}-x\right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x\cdot (x-1)}{x-1} \right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x^2-x}{x-1}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-70026c2aed1bb58a120f8c18423d9ef5_l3.png)
现在这两项具有相同的分母,我们可以将它们分组:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2-(x^2-x)}{x-1} \right] =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-7702287a02af6d8e3dddaa3f0c6eb1b5_l3.png)
最后我们解决极限:
![Rendered by QuickLaTeX.com \displaystyle n =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right] = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-feb5faa9dc5d3b68d3273ad4d75d2bb1_l3.png)
因此 n = 1。因此斜渐近线为:
![]()
![]()
![]()
一旦我们计算了斜渐近线,我们就通过制作一个值表将其表示在同一张图表上:
![]()

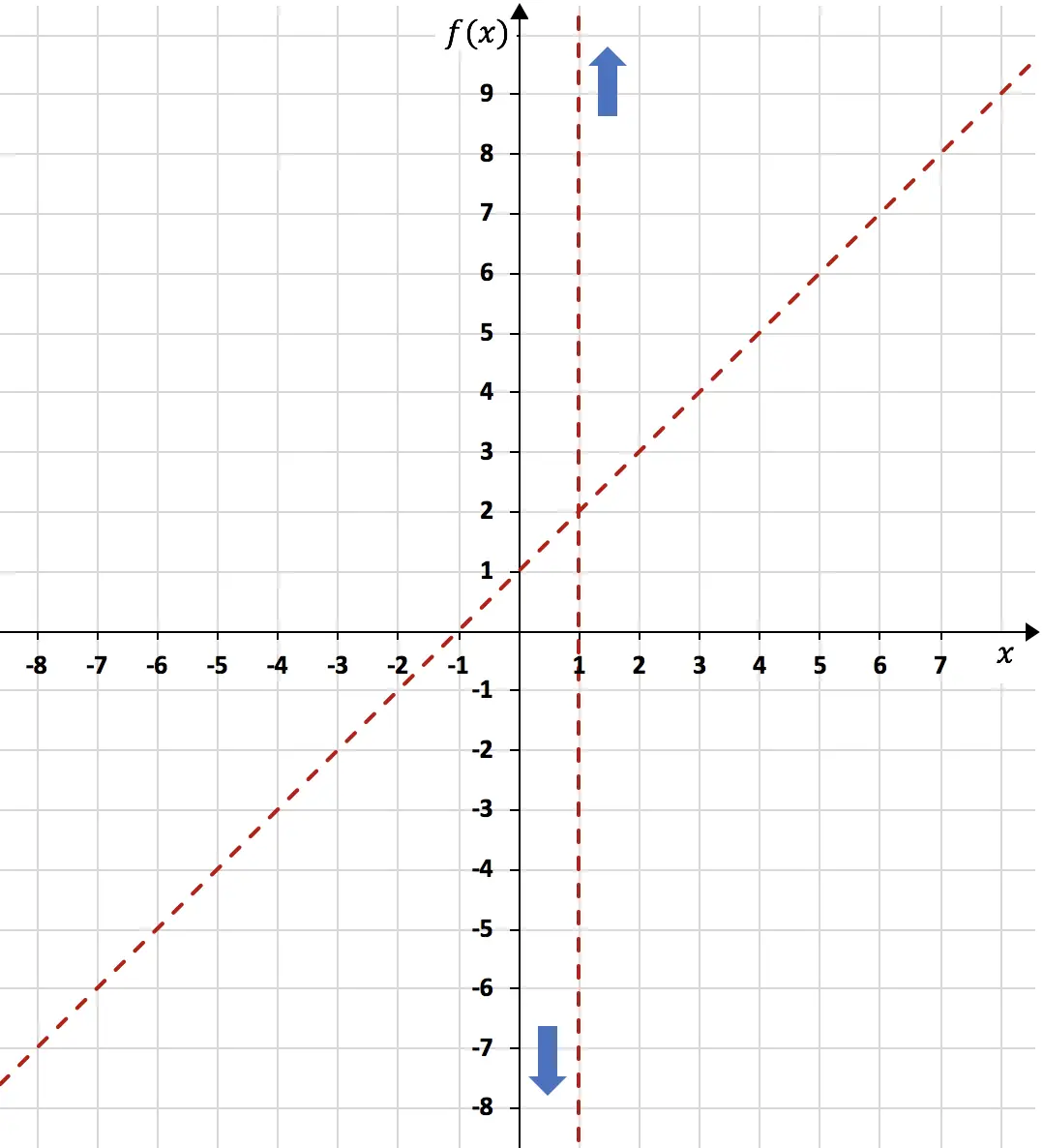
现在我们知道了函数的所有渐近线,我们需要分析函数的单调性。也就是说,我们需要研究函数在哪些区间增加以及在哪些区间减少。因此,我们计算函数的一阶导数:
![]()
![]()
现在我们将导数设置为 0 并求解方程:
![]()
![]()
期限
![]()
这涉及到将整个左侧除,因此我们可以将其乘以整个右侧:
![]()
![]()
我们提取公因子来求解二次方程:
![]()
为了使乘法等于 0,乘法的两个元素之一必须为零。因此,我们将每个因子设置为0,并得到方程的两个解:
![Rendered by QuickLaTeX.com \displaystyle x\cdot(x-2) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] x-2=0 \ \longrightarrow \ \bm{x= 2} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55127e675ce8f7742db17d565c2ae507_l3.png)
现在我们在数轴上表示所有找到的临界点,即不属于定义域的点 (x=1) 和取消导数的点 (x=0 和 x=2):

我们评估每个区间内导数的符号,以了解函数是增加还是减少。因此,我们在每个区间取一个点(而不是临界点)并查看导数在该点的符号:
![]()
![]()
![]()
![]()
![]()
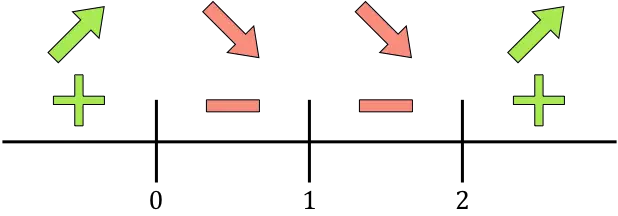
如果导数为正,则表示函数在增,如果导数为负,则表示函数在减。因此,增长区间和下降区间为:
生长:
![]()
减少:
![]()
此外,当 x=0 时,函数从增加变为减少,因此 x=0 是函数的相对最大值。当 x=2 时,函数从递减变为递增,因此 x=2 是函数的相对最小值。
最后,我们将找到的极值代入原始函数以找到点的 Y 坐标:
![]()
![]()
因此,该函数的相对极值是:
最大接通点
![]()
最小到点
![]()
我们在图表上表示最大值和最小值:
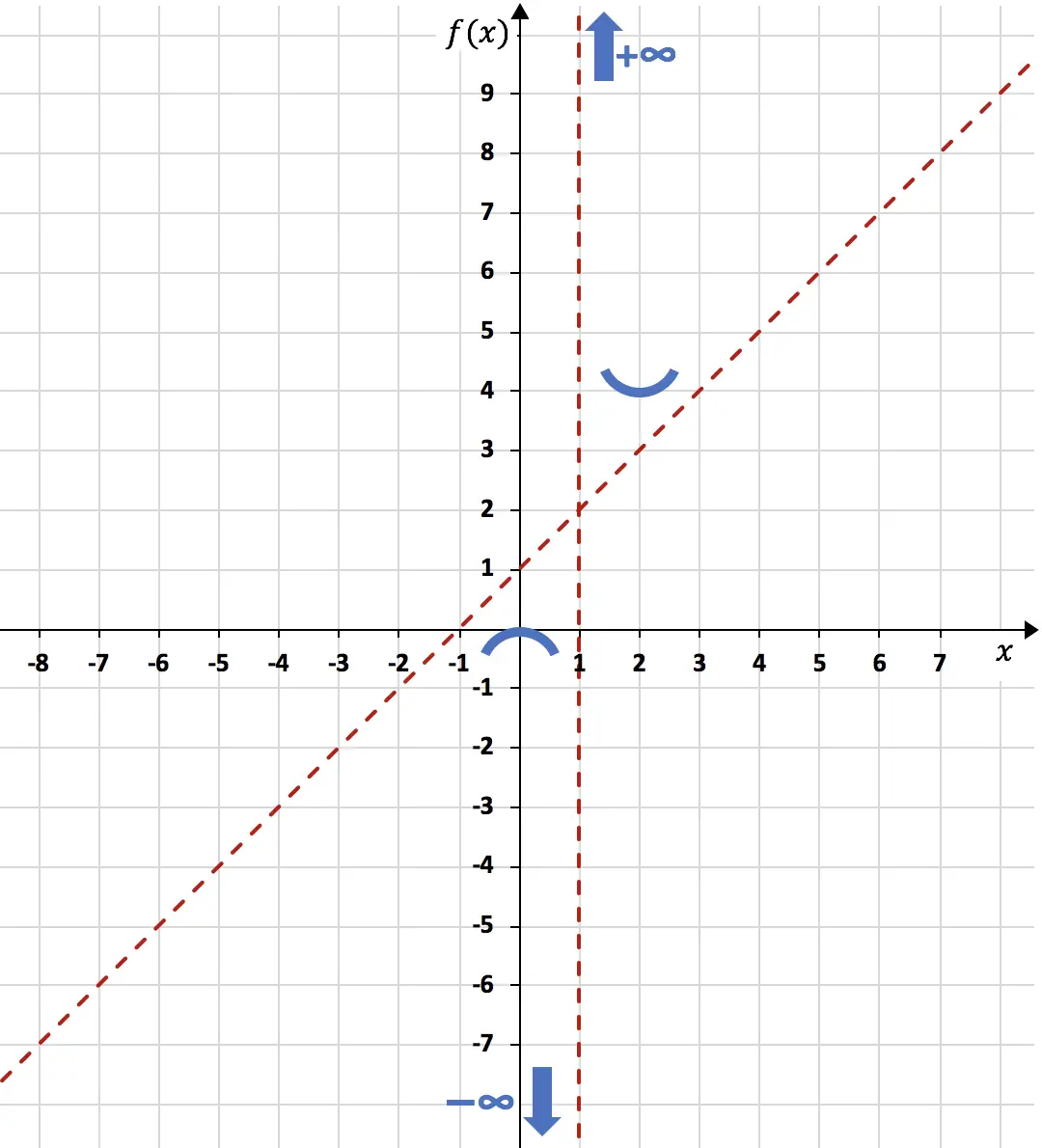
最后,研究函数的曲率就足够了,也就是说研究函数的凹凸区间。为此,我们计算其二阶导数:
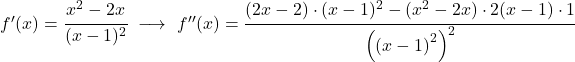
![]()
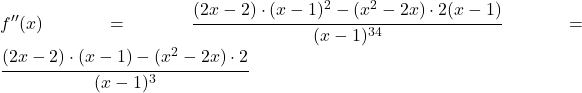
![]()
![]()
现在我们将二阶导数设置为零并求解方程:
![]()
![]()
![]()
![]()
2 永远不会等于 0,所以等式
![]()
没有解决办法。
现在,我们在数轴上表示所有找到的临界点,也就是说,不属于定义域 (x=1) 的点和取消二阶导数的点(在这种情况下,没有一个点不是):

然后我们评估每个区间内导数的符号,以了解该函数是凸函数还是凹函数。因此,我们在每个区间中取一个点(而不是奇点)并查看此时导数的符号:
![]()
![]()
![]()

最后推导出函数的凹凸区间。如果二阶导数为正,则表示该函数是凸函数。
![]()
,如果二阶导数为负,则意味着该函数是凹函数
![]()
。因此,凹度和凸度区间为:
凸面
![]()
:
![]()
凹
![]()
:
![]()
然而,即使 x=1 处曲率发生变化,它也不是拐点。因为x=1不属于函数的定义域。
所以我们可以使用我们计算的所有内容来完成表示函数:
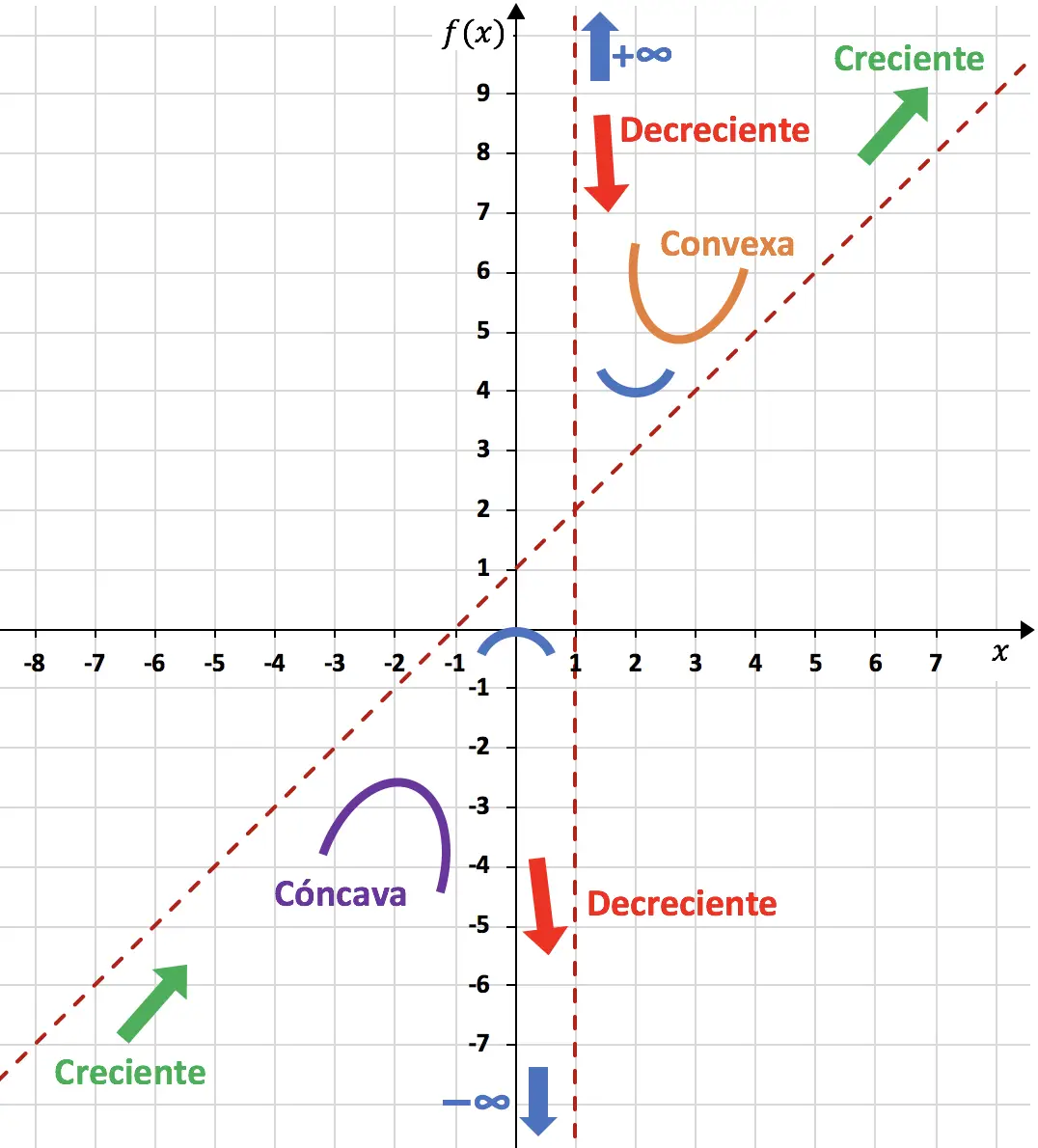
因此,图表上表示的函数如下所示:
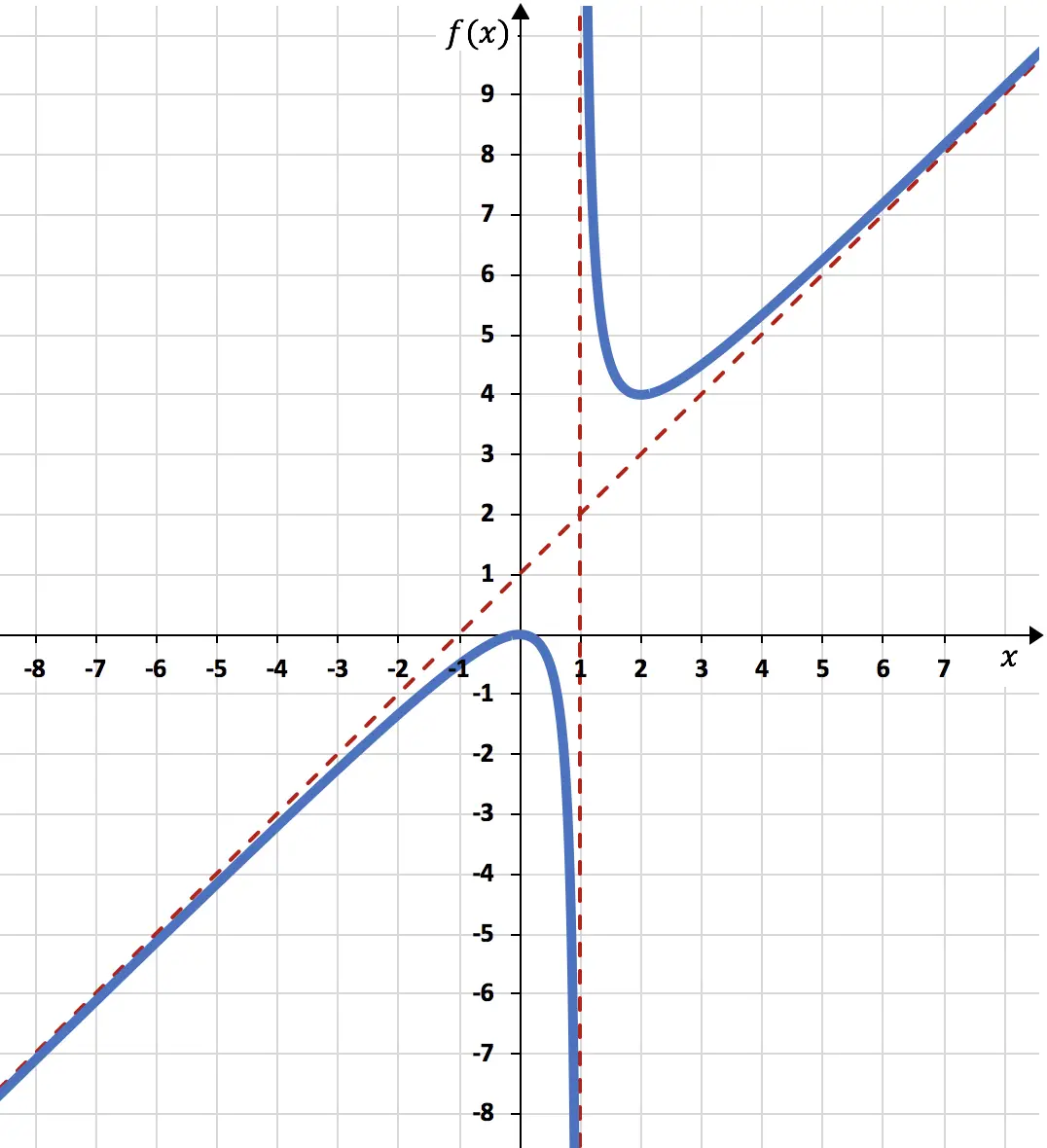
解决了表示函数的练习
练习1
绘制以下多项式函数的图形:
![]()
首先要做的是计算函数的定义域。这是一个多项式函数,因此域仅由实数组成:
![]()
为了找到与 X 轴的交点,我们求解
![]()
![]()
![]()
这是一个大于 2 次的方程。因此,我们对方程进行因式分解:
![]()
所以x=-1是一个解。我们通过求解所得到的二次方程来计算其他解:
![Rendered by QuickLaTeX.com \begin{aligned}x & =\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1 \cdot 4}}{2\cdot 1} \\[2ex] &=\cfrac{+4 \pm \sqrt{16-16}}{2} =\cfrac{4 \pm \sqrt{0}}{2} = \cfrac{4 }{2 } = 2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e79a2a2f6650c4095c0dca52188c40c3_l3.png)
因此与 X 轴的交点为:
![]()
和
![]()
为了找到与 Y 轴的交点,我们计算
![]()
由于 x 在 Y 轴上始终为 0:
![]()
因此与 Y 轴的交点为:
![]()
要查看函数是否具有垂直渐近线,我们需要计算函数在不属于定义域的点处的极限。在这种情况下,域包括所有实数。因此该函数没有垂直渐近线。
另一方面,函数的水平渐近线将是函数无限极限的结果。然而:
![]()
函数的无限极限给了我们+∞,因此函数没有水平渐近线。
我们现在计算斜渐近线。斜渐近线的形式为
![]()
和
![]()
其计算公式如下:
![]()
![]()
极限给了我们+∞,因此该函数也没有斜渐近线。
为了研究函数的单调性,我们首先要计算它的导数:
![]()
现在我们将导数设置为 0 并求解方程:
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x\cdot(3x-6) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] 3x-6=0 \ \longrightarrow \ x= \cfrac{6}{3} = 2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d23e2b378508baca9f51117fc8767e90_l3.png)
现在,我们在数轴上表示所有获得的奇异点,即不属于定义域的点(在本例中,它们都属于)和取消导数的点(x=0 和 x=2) :

我们评估每个区间内导数的符号,以了解函数是增加还是减少。因此,我们在每个区间中取一个点(而不是奇点)并查看此时导数的符号:
![]()
![]()
![]()

如果导数为正,则表示函数在增,如果导数为负,则表示函数在减。因此,增长区间和下降区间为:
生长:
![]()
减少:
![]()
该函数在 x=0 处从增加变为减少,因此 x=0 是该函数的最大值。当 x=2 时,函数从递减变为递增,因此 x=2 是函数的最小值。
最后,我们将找到的极值代入原始函数以求出点的 Y 坐标:
![]()
![]()
因此,该函数的相对极值是:
最大接通点
![]()
最小到点
![]()
为了研究函数的曲率,我们计算它的二阶导数:
![]()
现在我们将二阶导数设置为 0 并求解方程:
![]()
![]()
![]()
![]()
我们在线上表示所有找到的奇异点,也就是说,不属于定义域的点(在这种情况下它们都属于)和取消导数的点(x=1):

现在我们评估每个区间内的二阶导数的符号,以了解该函数是凹函数还是凸函数。因此,我们在每个区间中取一个点(而不是奇点)并查看此时二阶导数的符号:
![]()
![]()

如果二阶导数为正,则表示该函数是凸函数。
![]()
,如果二阶导数为负,则意味着该函数是凹函数
![]()
。因此,凹度和凸度区间为:
凸面
![]()
:
![]()
凹
![]()
:
![]()
另外,函数在 x=1 处由凹变为凸,因此 x=1 是函数的拐点。
最后,我们将找到的拐点代入原函数,求出这些点的 Y 坐标:
![]()
因此,函数的转折点为:
转折点:
![]()
最后,根据我们计算出的所有信息,我们绘制函数图:
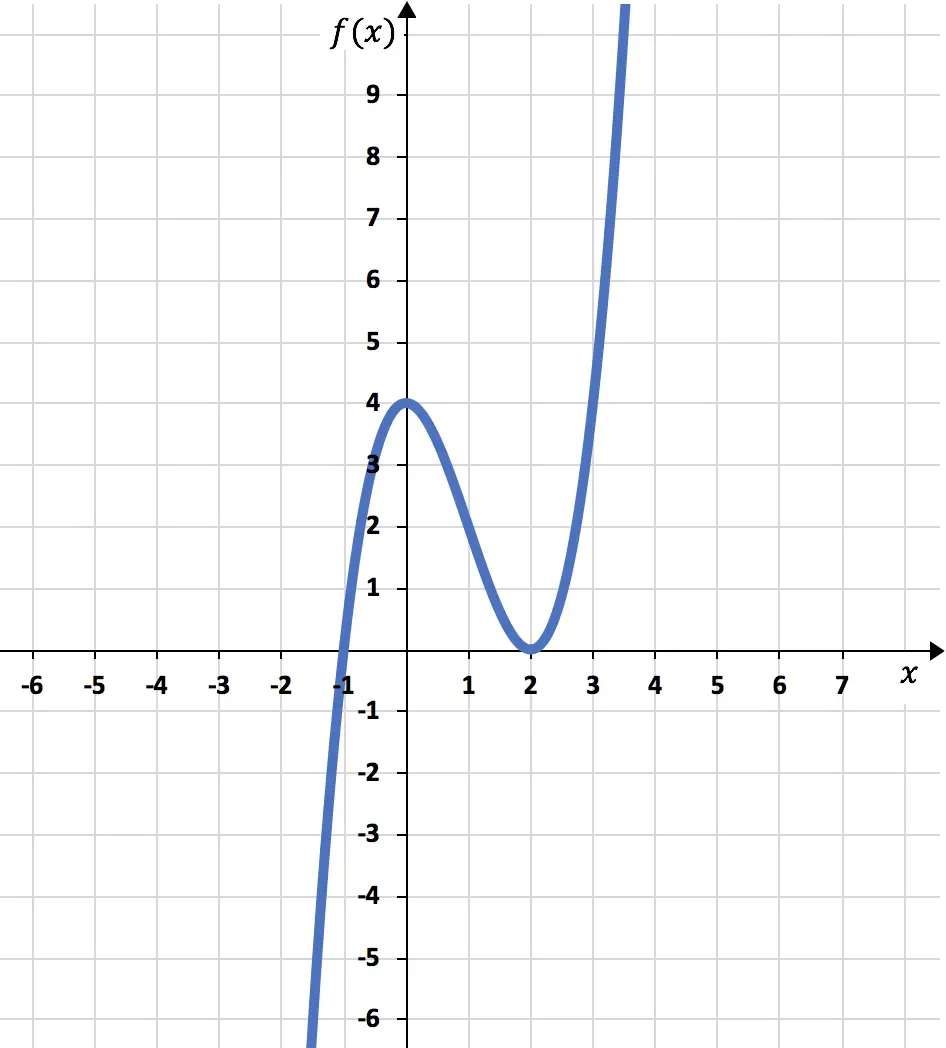
练习2
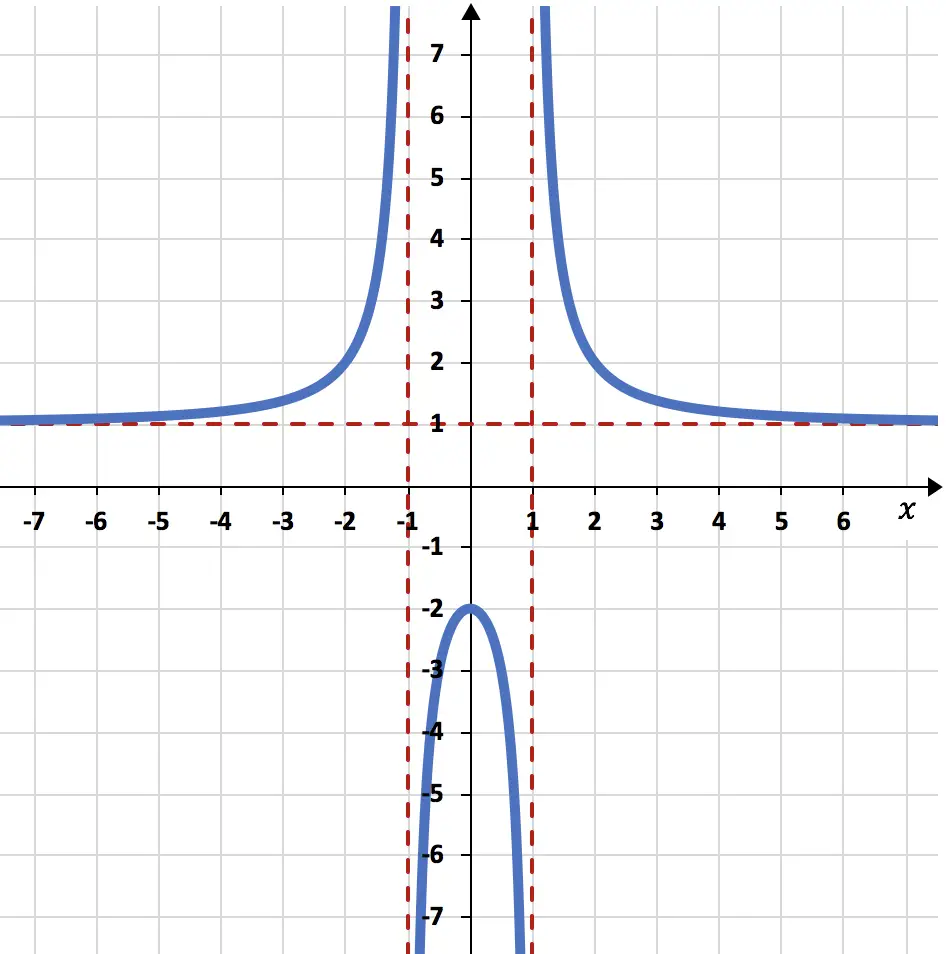
画出以下有理函数的图形:
![]()
为了找到函数的定义域,我们将分母设置为相等。将分数归零并求解所得方程:
![]()
![]()
![]()
![]()
![]()
其次,我们确定函数的阈值,其中 x 轴等于函数的代数表达式。钢:
![]()
![]()
![]()
![]()
![]()
![]()
负数没有平方根。因此,该函数不与 X 轴相交。
为了找到与计算机轴的交点,我们在 x=0 处计算函数。
![]()
因此与 Y 轴的交点为:
![]()
要查看函数是否具有垂直渐近线,我们需要计算函数在不属于定义域的点处的极限(在本例中为 x=-1 和 x=+1)。如果结果是无穷大,则它是垂直渐近线。然而:
![]()
由于当 x 接近 -1 时函数的极限给出无穷大,因此 x=-1 是垂直渐近线。
我们通过将一个非常接近它的数字代入函数来计算渐近线 x=-1 的横向极限:
![]()
![]()
现在让我们看看 x=+1 是否是垂直渐近线:
![]()
由于当 x 接近 +1 时函数的极限给出无穷大,因此 x=+1 是垂直渐近线。
我们通过将一个非常接近它的数字代入函数来计算渐近线 x=1 的横向极限:
![]()
![]()
另一方面,函数的水平渐近线将是函数无限极限的结果。然而:
![]()
该函数的无限极限为 1,因此该函数在 y=1 处有一条水平渐近线。
由于该函数具有水平渐近线,因此不会有斜渐近线。
我们对函数进行微分,然后研究增长和下降的区间:
![]()
![]()
现在我们将导数设置为 0 并求解方程:
![]()
![]()
![]()
![]()
![]()
我们在线上表示所有计算出的临界点,这些点是不属于定义域的点(x=-1 和 x=+1)以及取消导数的点(x=0):

我们评估每个区间内导数的符号,以了解函数是增加还是减少。因此,我们在每个区间中取一个点(而不是奇点)并查看此时导数的符号:
![]()
![]()
![]()
![]()
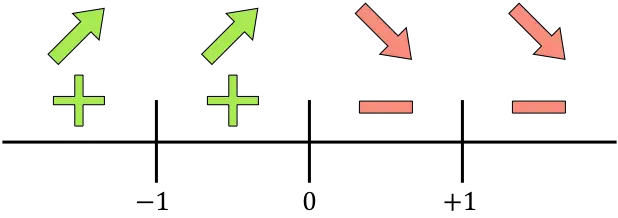
当导数为正时,函数增大;当函数为负时,函数减小:
生长:
![]()
减少:
![]()
该函数在 x=0 处从增加变为减少,因此 x=0 是该函数的局部最大值。
将找到的极值代入原函数即可求出该点的Y坐标:
![]()
因此,该函数的相对极值是:
最大接通点
![]()
为了研究函数的曲率,我们计算它的二阶导数:
![f'(x)=\cfrac{-6x}{\left(x^2-1 \right)^2} \ \longrightarrow <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-273969cf60ee8cf3413ee2f8b1db7688_l3.png" height="129" width="476" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f''(x)= \cfrac{-6 \cdot \left(x^2-1 \right)^2 - (-6x) \cdot 2(x^2-1) \cdot 2x}{ \left(\left(x^2-1 \right)^2\right)^2}$$ f''(x)= \cfrac{-6 \left(x^2-1 \right)^2 -(-6x)\cdot 4x(x^2-1)}{\left(x^2 -1\right)^4} =\]" title="Rendered by QuickLaTeX.com"/> \cfrac{-6 \left(x^2-1 \right)^2 + 24x^2(x^2-1)}{\left(x^2 -1\right)^4}” title=”Rendered by QuickLaTeX.com”></p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-802852beb818dd5a0dce2f30374f3a88_l3.png) 所有条款都有
所有条款都有
![]()
,因此我们可以简化分数:
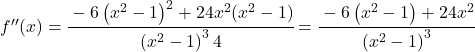
![]()
现在我们将二阶导数设置为 0 并求解方程:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
负数没有平方根。所以没有匹配的点
![]()
现在我们在线上表示所有找到的奇异点,即不属于定义域的点(x=-1 和 x=+1)以及取消二阶导数的点(在这种情况下没有任何):
我们评估每个区间内的二阶导数的符号,以了解该函数是凹函数还是凸函数。因此,我们在每个区间中取一个点(而不是奇点)并查看此时二阶导数的符号:
![]()
![]()
![]()

如果二阶导数为正,则表示该函数是凸函数。
![]()
,如果二阶导数为负,则意味着该函数是凹函数
![]()
。因此,凹度和凸度区间为:
凸面
![]()
:
![]()
凹
![]()
:
![]()
然而,尽管在 x=-1 和 x=1 处曲率发生变化,但这些都不是拐点。因为它们不属于函数域。
最后,我们使用执行的所有计算绘制函数图:
练习3
在图上绘制以下有理函数:
![]()
这是一个有理函数,所以我们需要将分母设置为0,看看哪些数字不属于函数的定义域:
![]()
![]()
![]()
![]()
![]()
为了找到与 X 轴的交点,我们求解
![]()
由于该函数在 X 轴上的值始终为 0:
![]()
![]()
![]()
![]()
![]()
因此与 X 轴的交点为:
![]()
为了找到与 Y 轴的交点,我们计算
![]()
由于 x 在 Y 轴上始终为 0:
![]()
因此与 Y 轴的交点为:
![]()
在这种情况下,由于函数经过坐标原点,因此与 X 轴的交点与与 Y 轴的交点重合。
要查看函数是否具有垂直渐近线,我们需要计算函数在不属于定义域的点处的极限(在本例中为 x=-2 和 x=+2)。如果结果是无穷大,则它是垂直渐近线。然而:
![]()
由于当 x 接近 -2 时函数的极限给出无穷大,因此 x=-2 是垂直渐近线。
我们通过将一个非常接近它的数字代入函数来计算渐近线 x=-2 的横向极限:
![]()
![]()
现在让我们看看 x=+2 是否是垂直渐近线:
![]()
由于当 x 接近 +2 时函数的极限给出无穷大,因此 x=+2 是垂直渐近线。
我们通过将一个非常接近它的数字代入函数来计算渐近线 x=2 的横向极限:
![]()
![]()
另一方面,函数的水平渐近线将是函数无限极限的结果。然而:
![]()
函数的无限极限给了我们+∞,因此函数没有水平渐近线。
我们现在计算斜渐近线。斜渐近线的形式为
![]()
和
![]()
其计算公式如下:
![]()
![]()
![]()
一旦我们知道斜渐近线的斜率,我们就可以使用以下公式确定截距:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[f(x)-mx\right] = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-1x\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-de4326a40acf34b64a28c9da8250bf00_l3.png)
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}](https://mathority.org/wp-content/ql-cache/quicklatex.com-13478ac6f6fac958ec8b2a714c28bc3d_l3.png)
但我们得到了不确定性 ∞ – ∞。因此,有必要将这些术语简化为一个公分母。为此,我们将 x 除以分数的分母:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x \cdot (x^2-4)}{(x^2-4)}\right] =\lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x^3-4x}{x^2-4}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e939b43a3405ba644d4b60bb4bacadb_l3.png)
![]()
![]()
简而言之,斜渐近线是:
![]()
![]()
![]()
为了研究函数的单调性,我们首先要计算它的导数:
![]()
![]()
现在我们将导数设置为 0 并求解方程:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x^2\cdot(x^2-12) =0 \longrightarrow \begin{cases} x^2 =0 \ \longrightarrow \ \bm{x=0} \\[2ex] x^2-12=0 \ \longrightarrow \ x=\sqrt{12} \ \longrightarrow \ \bm{x= \pm 3,46} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc1f64cdcd293da4fee1ef02fff9a588_l3.png)
现在,我们在线上表示所有找到的奇异点,即不属于定义域的点(x=-2 和 x=+2)以及取消导数的点(x=0,x=- 3.46 且 x= +3.46):

我们评估每个区间内导数的符号,以了解函数是增加还是减少。因此,我们在每个区间中取一个点(而不是奇点)并查看此时导数的符号:
![]()
![]()
![]()
![]()
![]()
![]()
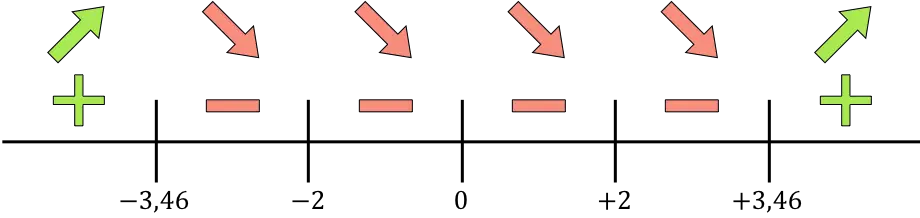
如果导数为正,则表示函数在增,如果导数为负,则表示函数在减。因此,增长区间和下降区间为:
生长:
![]()
减少:
![]()
该函数在 x=-3.46 处从增加变为减少,因此 x=-3.46 是该函数的最大值。当 x=3.46 时,函数从递减变为递增,因此 x=3.46 是函数的最小值。
我们确定相对端的 Y 坐标:
![]()
![]()
因此,该函数的相对极值是:
最大接通点
![]()
最小到点
![]()
为了研究函数的曲率,我们计算函数的二阶导数:



![]()
![]()
![]()
![]()
现在我们将二阶导数设置为 0 并求解方程:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31adba554b44aa92fd7227506440ccaf_l3.png)
![]()
没有解,因为实数没有负根。
现在我们在线上表示所有找到的奇异点,即不属于定义域的点(x=-2 和 x=+2)以及取消二阶导数的点(x=0):

我们评估每个区间内的二阶导数的符号,以了解该函数是凹函数还是凸函数。因此,我们在每个区间中取一个点(而不是奇点)并查看此时二阶导数的符号:
![]()
![]()
![]()
![]()

如果二阶导数为正,则表示该函数是凸函数。
![]()
,如果二阶导数为负,则意味着该函数是凹函数
![]()
。因此,凹度和凸度区间为:
凸面
![]()
:
![]()
凹
![]()
:
![]()
然而,尽管在 x=-2 和 x=+2 处曲率发生变化,但这些都不是拐点。因为x=-2和x=+2不属于函数的定义域。另一方面,在 x=0 处,曲率发生变化(函数从凸变为凹),这属于函数,因此 x=0 是拐点。
我们将找到的拐点代入原函数,求出拐点的另一个坐标:
![]()
因此,函数的转折点为:
转折点:
![]()
最后,根据我们计算出的所有信息,我们表示该函数:
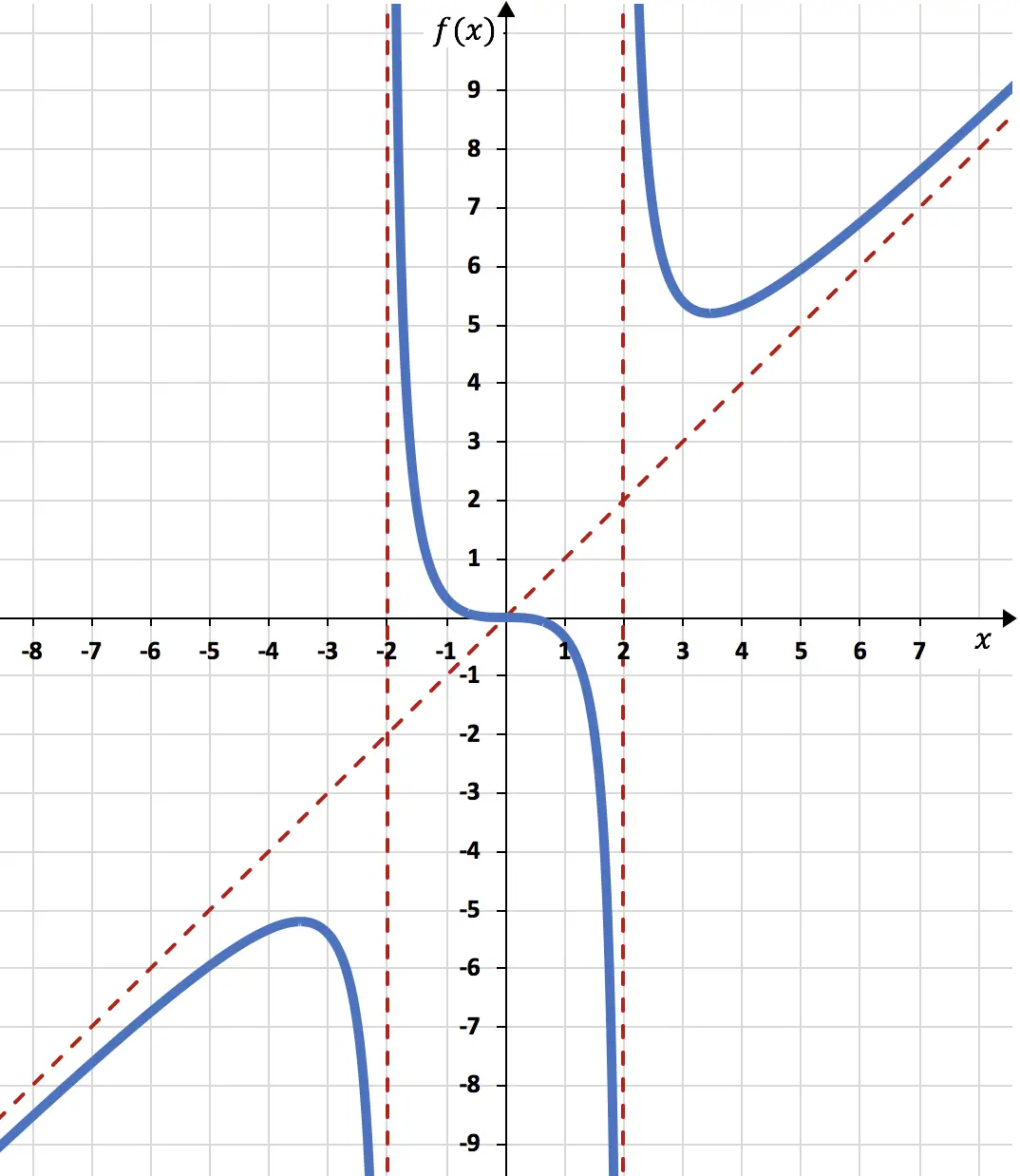
注释:注意函数在点处穿过斜渐近线
![]()
事实上,斜渐近线首先决定了当 x 趋于 + 和 – 时函数的所有行为,事实上,函数永远不会穿过图右侧 (x→+∞) 和左侧的斜渐近线。图 (x→-∞)。然而,函数穿过中间的斜渐近线的情况很少见,这是一种非常特殊的情况。