▷ 函数的复合（或复合函数）

在本文中，我们将解释什么是复合函数（或函数的组合）。此外，您将能够看到复合函数的几个示例以及如何计算此类函数的域。最后，您将找到函数组合的属性和几个可供练习的分步练习。

什么是函数组合？

函数组合包括在两个或多个函数中连续评估自变量 (x) 的相同值。例如，复合函数 (gof)(x) 给出复合函数 g[f(x)]。

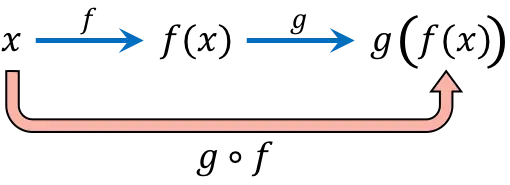
复合函数的表达式

$g\circ f$

我们读“f 由 g 组成”或“f 后跟 g”。

请注意，函数组合中的顺序很重要，首先应用组合符号右侧的函数

$(f)$

然后是组合符号左边的函数

$(g).$

函数组合示例

给定复合函数的定义，让我们看一个如何计算两个函数的复合的示例。

给出以下两个不同的函数：

$f(x)=3x+1 \qquad g(x)=\cfrac{x+4}{2}$

计算复合函数

$\left(g \circ f\right)(x)$

并对其进行评估

$x=3.$

函数的组成

$\left(g \circ f\right)(x)$

这意味着我们需要执行以下复合函数：

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

为了解决这个问题，我们替换

$f(x)$

由其代数表达式：

$g\Big(f(x)\Big)= g\Big(3x+1\Big)$

现在我们取函数

$g(x)=\cfrac{x+4}{2}$

我们把表达式

$3x+1$

哪里有一个

$x:$

$g\Big(3x+1\Big)=\cfrac{(3x+1)+4}{2}=\cfrac{3x+5}{2}$

这样我们就已经计算出了由g组成的函数f ：

$\left(g \circ f\right)(x)=\cfrac{3x+5}{2}$

最后，评估复合函数

$x=3$

简单地计算该值中函数的图像：

$\left(g \circ f\right)(3)=\cfrac{3\cdot 3+5}{2}=\cfrac{14}{2}=7$

复合函数域

通常，当我们对函数进行运算时，结果函数的域是原始函数域的交集。然而，函数组合并不能满足这个性质。

函数复合的域

$(g\circ f)(x)$

相当于函数域内x所有值的集合

$f$

例如

$f(x)$

属于函数域

$g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

因此，要计算复合函数的定义域，必须首先分别求出每个函数的定义域，然后再求运算得到的函数的定义域。因此，函数的复合域将由满足先前数学条件的所有值组成。

👉记住，如果您遇到不知道如何解决的问题，可以在下面的评论中询问我们！

函数组合的性质

复合函数具有以下特点：

函数的复合具有结合性质，因此，以下等式始终成立：

$f\circ (g\circ h)=(f\circ g)\circ h$

一般来说，函数组合是不可交换的，因此运算的顺序决定了结果：

$f\circ g\neq g\circ f$

函数复合的中性元素对应于恒等函数
$f(x)=x.$

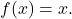
因此，任何由恒等函数组成的函数都会产生函数本身：

$f\circ id = id \circ f = f$

$id = x$

计算两个函数的复合函数的逆函数相当于首先找到每个函数的逆函数，然后确定复合函数：

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

反函数也充当复合函数的对称元素，因为函数与其反函数的复合等价于恒等函数：

$(f\circ f^{-1})^{-1}=(f^{-1}\circ f)=id=x$

使用链式法则计算两个函数复合的导数：

$\bigl(g\circ f\bigr)'(x)=g'\Bigl(f(x)\Bigr)\cdot f'(x)$

➤看：什么是链式法则？

解决了函数组合的练习

练习1

给定以下两个函数：

$f(x)=x-2 \qquad g(x)= 5x + 4$

计算由g组成的函数f以及由f组成的g 的复合。

$(g\circ f)(x)$

$(f\circ g)(x)$

查看解决方案

函数的组成

$\left(g \circ f\right)(x)$

意味着计算以下复合函数：

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

所以为了解决这个问题，我们替换

$f(x)$

其表达方式为：

$f(x)=x-2$

$g\Big(f(x)\Big)= g\Big(x-2\Big)$

和

$g\Big(x-2\Big)$

这意味着在表达式中

$g(x) =5x+4$

你需要替换变量

$x$

为了

$x-2:$

$g\Big(x-2\Big) = 5(x-2) +4= 5x-10+4 = 5x-6$

然而：

$\bm{\left(g \circ f\right)(x) = 5x-6}$

另一方面，要找到由f组成的函数g ，您必须执行相同的过程，但顺序相反：

$\begin{aligned}\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&=f\Big(5x+4\Big)\\[2ex]&=(5x+4)-2\\[2ex]&=\bm{5x+2}\end{aligned}$

此练习还演示了复合函数不可交换的属性，因为结果取决于应用函数的顺序。

练习2

给定以下两个函数：

$\displaystyle f(x) =x^2-3 \qquad g(x)=\frac{2x+3}{x+4}$

计算由g组成的函数f的复合。

$(g\circ f)(x)$

查看解决方案

由g组成的函数f表示求解如下复合函数：

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

因此，我们将函数 f(x) 替换为其表达式：

$g\Big(f(x)\Big)= g\Big(x^2-3 \Big)$

现在我们必须更换

$x$

为了

$x^2-3$

在函数g(x)的表达式中：

$\begin{aligned}g\Big(x^2-3\Big)&=\cfrac{2(x^2-3)+3}{(x^2-3)+4}\\[2ex]&=\cfrac{2x^2-6+3}{x^2+1}\\[2ex]&=\cfrac{2x^2-3}{x^2+1}\end{aligned}$

简而言之，函数复合的结果是：

$\bm{\left(g \circ f\right)(x) =} \cfrac{\bm{2x^2-3}}{\bm{x^2+1}}$

练习3

给定以下两个二次函数：

$\displaystyle f(x) =x^2 \qquad g(x)=g(x)= x^2-4x+8$

确定下列函数组合的结果：

$(g\circ f)(2)$

查看解决方案

$\left(g \circ f\right)(2)$

包括找到以下复合函数：

$\left(g \circ f\right)(2) = g\Big(f(2)\Big)$

因此，为了求解复合函数，我们首先计算

$f(2) :$

$f(x)=x^2$

$f(2)=2^2=4$

因此，作为

$f(2)=4 :$

$\left(g \circ f\right)(2) = g\Big(f(2)\Big) = g\big(4\big)$

因此，要找到复合函数的值，您只需计算

$g(4) :$

$\begin{aligned}\left(g \circ f\right)(2)&=g\Big(f(2)\Big)\\[2ex]&= g\big(4\big)\\[2ex]&=4^2-4\cdot 4+8 \\[2ex]&= 16 - 16 + 8\\[2ex]&= 8\end{aligned}$

综上所述，函数组合问题的结果为：

$\bm{\left(g \circ f\right)(2) =8}$

练习4

给定以下两个函数：

$\displaystyle f(x)=\frac{2x-2}{-x+7}\qquad g(x)= x^2-1$

求g与f在 x=2 处的组合结果：

$(f\circ g)(2)$

查看解决方案

在这种情况下，我们必须计算以下复合函数：

$\left(f \circ g\right)(2) = f\Big(g(2)\Big)$

所以首先我们找到

$g(2) :$

$g(x)=x^2-1$

$g(2)=2^2-1=4-1 = 3$

所以，就像

$g(2)=3 :$

$\left(f \circ g\right)(2) = f\Big(g(2)\Big) = f\big(3\big)$

因此，为了求解复合函数，我们需要计算

$f(3) :$

$\begin{aligned}\left(f \circ g\right)(2)&=f\Big(g(2)\Big)\\[2ex]&= f\big(3\big)\\[2ex]&=\cfrac{2\cdot 3-2}{-3+7}\\[2ex]&=\cfrac{6-2}{-3+7}\\[2ex]&=\cfrac{4}{4}\\[2ex]&=1\end{aligned}$