在本文中,您将学习如何研究函数的可微性,即函数是否可微。此外,我们还将看到函数的可微性和连续性之间的关系。最后,我们将研究分段函数的可微性。
函数的可微性和连续性
函数在一点的连续性和可导性关系如下:
- 如果函数在一点可微,则该函数在该点连续。
- 如果函数在一点不连续,那么它在该点也是不可微的。
然而,该定理的逆命题是错误的:仅仅因为函数在一点连续,并不意味着它在该点总是可微的。
您还可以查看函数在某个点与其图形表示是否可微:
- 如果是平滑点,则函数在该点可微。
- 如果是角点,则函数在该点连续但不可微。
分段函数的可微性
一旦我们知道了函数的连续性和可微性之间的关系,我们就会了解如何研究分段定义函数的可微性。
您可以通过计算该点的横向导数来判断分段函数在该点是否可微:
注意:对于在一点可微的函数,该函数必须在该点连续。因此,在计算侧导数之前,我们需要保证函数在该点连续。如果您不知道如何研究某一点的连续性,您可以在以下链接中了解它是如何完成的:
➤请参见: 函数在一点的连续性
现在让我们看一个示例,了解如何计算在某一点分段定义的函数的导数:
- 研究以下在点 x=2 处分段定义的函数的连续性和可微性:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a98eee72521c68fd394eb6209a7d0a59_l3.png)
两部分的函数在各自的区间内连续,但需要看函数在临界点x=2处是否连续。为此,我们求解函数在该点的横向极限:
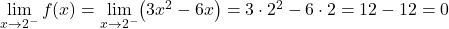
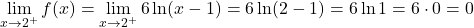
临界点处的横向极限给了我们相同的结果,因此函数在 x=2 点处连续。
一旦我们知道函数在 x=2 处连续,我们将研究函数在该点的可微性。为此,我们计算分段定义的函数的侧导数:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3709995609d0f69f382ff651e397c00a_l3.png)
我们现在评估临界点处的每个侧导数:
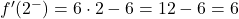
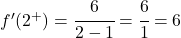
两个横向导数给出了相同的结果,因此函数在 x=2 处可微,导数值为 6:
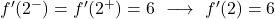
另一方面,如果横向导数给了我们不同的结果,则意味着该函数在 x=2 处不可微。换句话说,此时导数将不存在。
最后,请记住,此过程对于研究绝对值函数的可微性也有效,因为绝对值函数也可以分段定义。您可以在此处了解如何将绝对值函数转换为块:
➤请参阅: 如何分段定义具有绝对值的函数
解决了函数可微性的练习
练习1
研究以下分段函数的连续性和可导性:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} x^3-4x^2 + 5 & \text{si} & x<1 \\[2ex] -x^2+3x & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3656065bb8de98bd07da153f26fd326e_l3.png)
两部分的函数是连续的,但我们必须看函数在临界点x=1处是否连续。为此,我们求解函数在该点的横向极限:
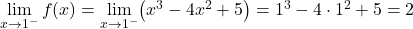
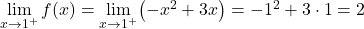
临界点处的两个横向极限给出相同的结果,因此该函数在 x=1 处连续。
一旦我们知道函数在临界点连续,我们就会研究它在同一点是否可微。因此我们计算横向导数:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 3x^2-8x & \text{si} & x<1 \\[2ex] -2x+3 & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-42451fa799527167fe9a2e2259248870_l3.png)
我们评估 x=1 处的两个侧导数;
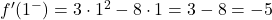
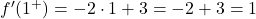
侧导数在 x=1 点处不重合,因此函数在该点不可微。
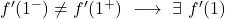
练习2
分析各节中定义的以下函数的可微性和连续性:
![\displaystyle f(x)= \left\{ \begin{array}{lcl} \sqrt{4x} & \text{si} & x\leq 1 \\[2ex] 2+\ln x & \text{si} & x> 1 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”226″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d118e3904c810abd15e427e9c7d0504_l3.png)
查看解决方案
两段函数在其区间上是连续的,但还需要知道函数在定义 x=1 变化的临界点是否连续。因此,我们此时定义函数的横向极限:
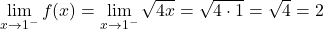
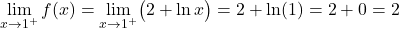
临界点处的两个横向极限给出相同的结果,因此该函数在 x=1 处连续。
现在我们通过计算侧导数来研究函数此时是否可微:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} \cfrac{4}{2\sqrt{4x}} & \text{si} & x<1 \\[4ex] \cfrac{1}{x} & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-8261f3d268b47d9171710997c8cc70bd_l3.png)
我们计算 x=1 处的两个侧导数:
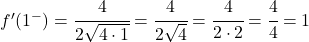
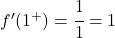
侧导数相等,因此函数在 x=1 处可微,导数值为 1。
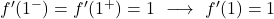
练习3
确定以下分段函数在其整个域上是否连续且可微:
*** QuickLaTeX cannot compile formula:
\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2+2x+1 & \text{si} & x\leq -1 \\[2ex] 2x+2 & \text{ si} & -1<div class="wp-block-otfm-box-spoiler-start otfm-sp__wrapper otfm-sp__box js-otfm-sp-box__closed otfm-sp__E6F9EF" role="button" tabindex="0" aria- expanded="false" data-otfm-spc="#E6F9EF" style="text-align:center"><div class="otfm-sp__title"> <strong>View solution</strong></div>< /div> The functions of all three parts are continuous, but we still need to check if the function is continuous at critical points. We therefore first check the continuity of the function at the point x=-1 by solving the lateral limits at this point:
*** Error message:
Missing $ inserted.
leading text: \displaystyle
Missing { inserted.
leading text: ...="wp-block-otfm-box-spoiler-start otfm-sp__
Missing { inserted.
leading text: ...ox-spoiler-start otfm-sp__wrapper otfm-sp__
Missing { inserted.
leading text: ...m-sp__wrapper otfm-sp__box js-otfm-sp-box__
Missing { inserted.
leading text: ...fm-sp__box js-otfm-sp-box__closed otfm-sp__
You can't use `macro parameter character #' in math mode.
leading text: ...="0" aria-expanded="false" data-otfm-spc="#
Missing { inserted.
leading text: ...e="text-align:center"><div class="otfm-sp__
Please use \mathaccent for accents in math mode.
leading text: ...g></div></div> The functions of the three parts
Please use \mathaccent for accents in math mode.
leading text: ...are continuous, but we still need to see
\lim\limits_{x\to -1^-} f(x) = \lim\limits_{x\to -1^-} \bigl(x^2+2x+1\bigr) = (-1)^ 2+2(-1)+1 =0 \lim\limits_{x\to -1^+} f(x) = \lim\limits_{x\to -1^+} \bigl(2x+2\bigr ) = 2(-1)+2=0
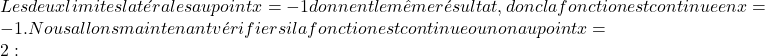
\lim\limits_{x\to 2^-} f(x) = \lim\limits_{x\to 2^-} \bigl(2x+2\bigr) = 2\cdot 2+2=4+2= 6 \lim\limits_{x\to 2^+} f(x) = \lim\limits_{x\to 2^+} \bigl( -x^2+8x\bigr) = -2^2+8\ cdot 2 = -4+16=12
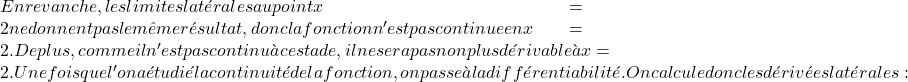
\displaystyle f'(x)= \left\{ \begin{array}{lcl} 2x+2 & \text{si} & x\leq -1 \\[2ex] 2 & \text{si} & -1
我们已经知道函数在 x=2 时不可微,因此我们只需要研究函数在 x=-1 时是否可微。为此,我们评估该点的两个侧导数:
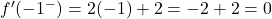
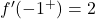
侧导数在 x=-1 点不重合,因此函数在该点不可微。
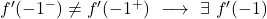
练习4
计算参数 a 和 b 的值,使以下分段函数在其整个域内连续且可微:
^2 & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce34d5d8a949fb3a0b904e9bf7d32f5b_l3.png)
无论未知数的值是多少,函数在除 x=3 处以外的所有点上都是连续且可微的,必须检查其连续性和可微性。
为了使函数在一点处连续,该点处的两个横向极限必须重合。因此,我们评估临界点的横向极限:
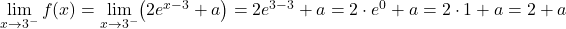
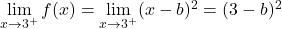
因此,从横向极限获得的两个值必须相等,函数才能连续:
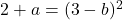
现在我们将分析点 x=3 处的可微性。我们求出横向导数:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 2e^{x-3} & \text{si} & x< 3 \\[2ex]2(x-b) & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d542fc9488644f0c144059ae1403d961_l3.png)
我们评估临界点处的两个侧导数:
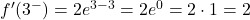
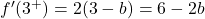
因此,为了使函数在 x=3 处可微,从侧导数获得的值必须相等:
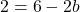
通过解这个方程我们可以找到 b 的值:
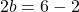
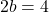
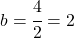
最后,一旦我们知道了参数b的值,我们就可以通过求解之前在横向极限中得到的方程来计算参数a的值:
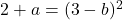
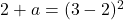
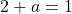
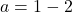
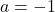


![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a98eee72521c68fd394eb6209a7d0a59_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3709995609d0f69f382ff651e397c00a_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} x^3-4x^2 + 5 & \text{si} & x<1 \\[2ex] -x^2+3x & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3656065bb8de98bd07da153f26fd326e_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 3x^2-8x & \text{si} & x<1 \\[2ex] -2x+3 & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-42451fa799527167fe9a2e2259248870_l3.png)
![]()
![]()
![]()
![\displaystyle f(x)= \left\{ \begin{array}{lcl} \sqrt{4x} & \text{si} & x\leq 1 \\[2ex] 2+\ln x & \text{si} & x> 1 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”226″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d118e3904c810abd15e427e9c7d0504_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} \cfrac{4}{2\sqrt{4x}} & \text{si} & x<1 \\[4ex] \cfrac{1}{x} & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-8261f3d268b47d9171710997c8cc70bd_l3.png)
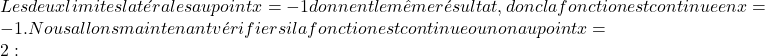
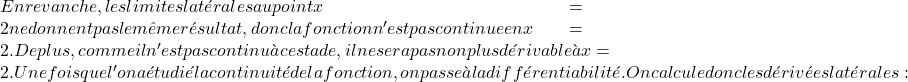
^2 & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce34d5d8a949fb3a0b904e9bf7d32f5b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 2e^{x-3} & \text{si} & x< 3 \\[2ex]2(x-b) & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d542fc9488644f0c144059ae1403d961_l3.png)