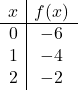本页解释什么是绝对值函数。您还将学习如何定义分段绝对值函数以及如何在图形上表示这些类型的函数。此外,您还将看到绝对值函数的示例,并且您将能够通过练习和逐步解决的问题进行练习。
什么是绝对值函数?
绝对值函数的定义如下:
函数的绝对值将其所有图像转换为正图像。因此,绝对函数的路径永远不能有负值。
以下函数是绝对值函数的示例:
![]()
如果在某个点评估函数时我们获得正结果,则它仍然是正值:
![]()
另一方面,如果结果为负,则变为正:
![]()
绝对值函数通常在高中给出,因为它们的特性使它们有点难以理解。
如何分段定义具有绝对值的函数
绝对值函数可以表示为分段函数。为此,您必须更改函数在负数区间上的符号。
让我们看一个如何从绝对值函数转换为分段函数的示例:
- 将以下具有绝对值的函数表示为分段函数:
![]()
我们需要做的第一件事是确定函数何时为负值。为此,我们将代数表达式的绝对值设置为 0 并求解方程:
![]()
![]()
![]()
![]()
![]()
我们现在表示线上获得的值:
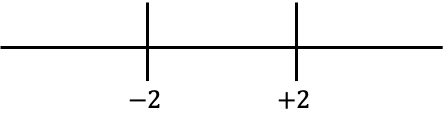
我们看看哪个符号在直线的每个区间内具有不带绝对值的函数:
![]()
例如,我们取任何小于-2的点
![]()
![]()
![]()
消极的
![]()
例如,我们取 -2 和 +2 之间的任意点
![]()
![]()
![]()
积极的
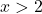
![]()
![]()
![]()
消极的

正如我们所看到的,没有绝对值的函数在区间上将为负值
![]()
和

![\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -(4-x^2) & \text{si} & x<-2 \\[2ex] 4-x^2 & \text{si} & -2 \le x \le 2 \\[2ex] -(4-x^2) & \text{si} & x>2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”372″ style=”vertical-align: 0px;”></p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5f441ea5792fb5cc7ba8300f71defef_l3.png)
![\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x<-2 \\[2ex] 4-x^2 & \text{si} & -2 \le x \le 2 \\[2ex] -4+x^2 & \text{si} & x>2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”358″ style=”vertical-align: 0px;”></p>
</p>
<p>请注意,在某些间隔中,您必须包含相等性。比如这里我们把它放在第二个区间</p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-89ab8a514afe36c94d7072efe47ef507_l3.png)
![]()
。但是,只要所有关键点都存在平局,您就可以将其放置在任何您想要的区间中。换句话说,如果我们将函数定义如下,结果是一样的:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x\le-2 \\[2ex] 4-x^2 & \text{si} & -2 < x < 2 \\[2ex] -4+x^2 & \text{si} & x\ge 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-5cce3bcc22edb3a7f511cea0a1c32372_l3.png)
如何用绝对值表示函数
为了在图形上表示具有绝对值的函数,我们需要遵循以下步骤:
- 将函数表示为没有绝对值。
- 在函数为负值(即位于 X 轴下方)的区间内,绘制对称函数。
- 删除 X 轴下方的函数部分。
让我们看一个如何绘制具有绝对值的函数的示例
- 画出下列函数的绝对值图:
![]()
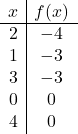
为了表示具有绝对值的函数,我们必须首先表示不具有绝对值的函数。因此,我们制作不带绝对值的函数值表:
![]()
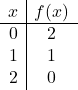
我们将点绘制成图表并绘制直线,就好像它是一个普通函数一样:
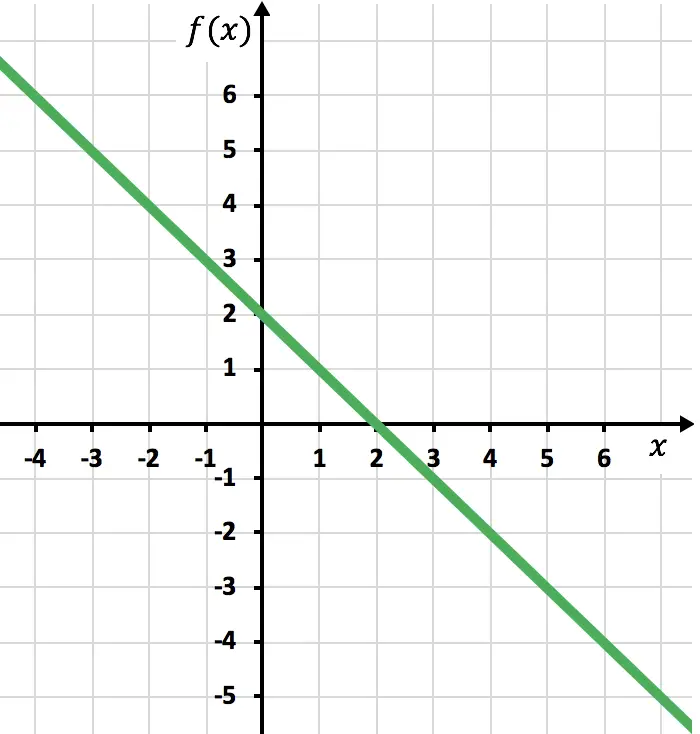
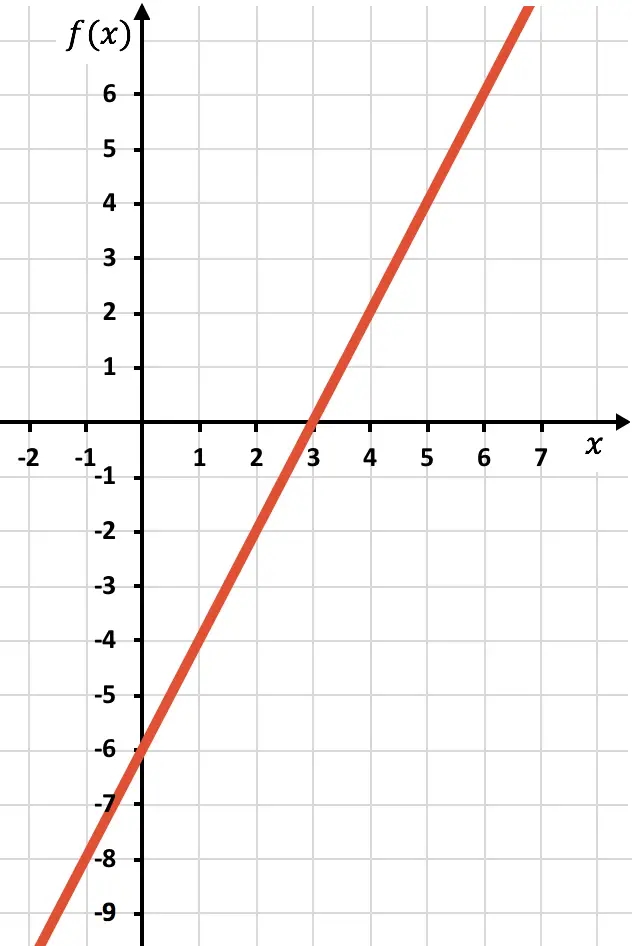
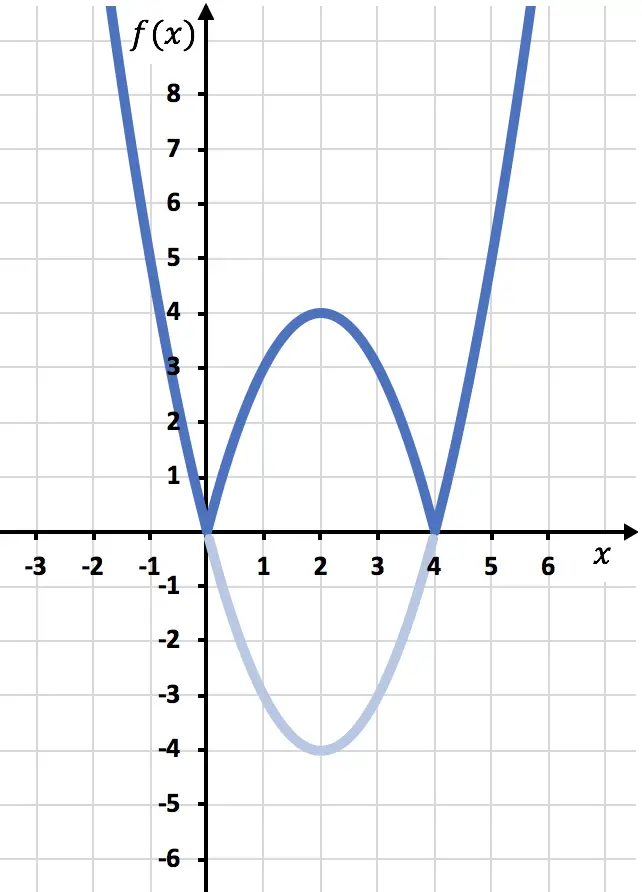
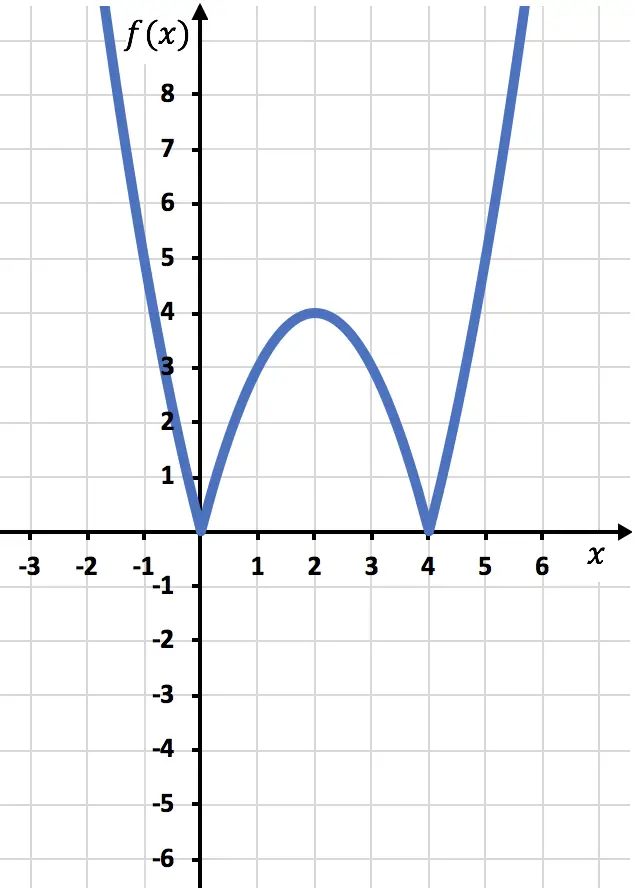
现在我们需要绘制函数为负的对称函数,即函数位于 x 轴下方的位置。因此,我们从 x=2 开始反转函数:
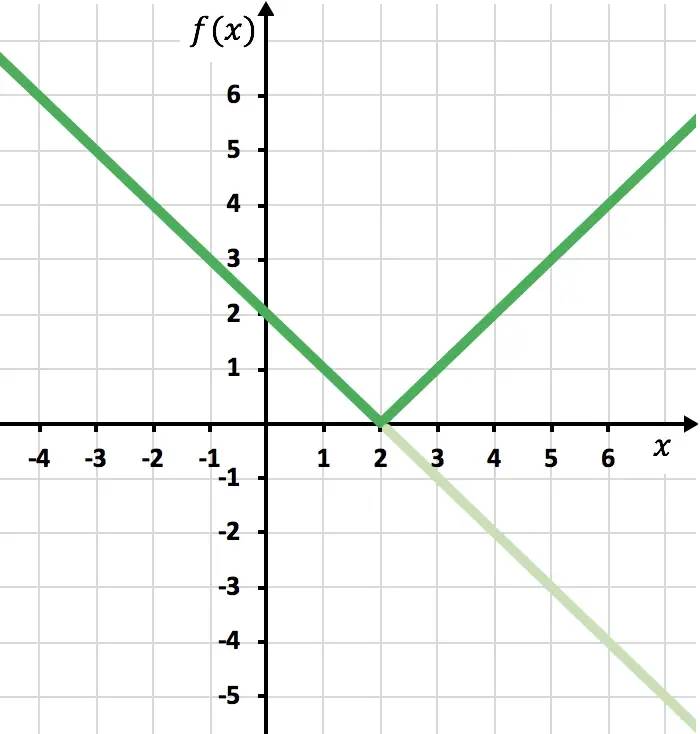
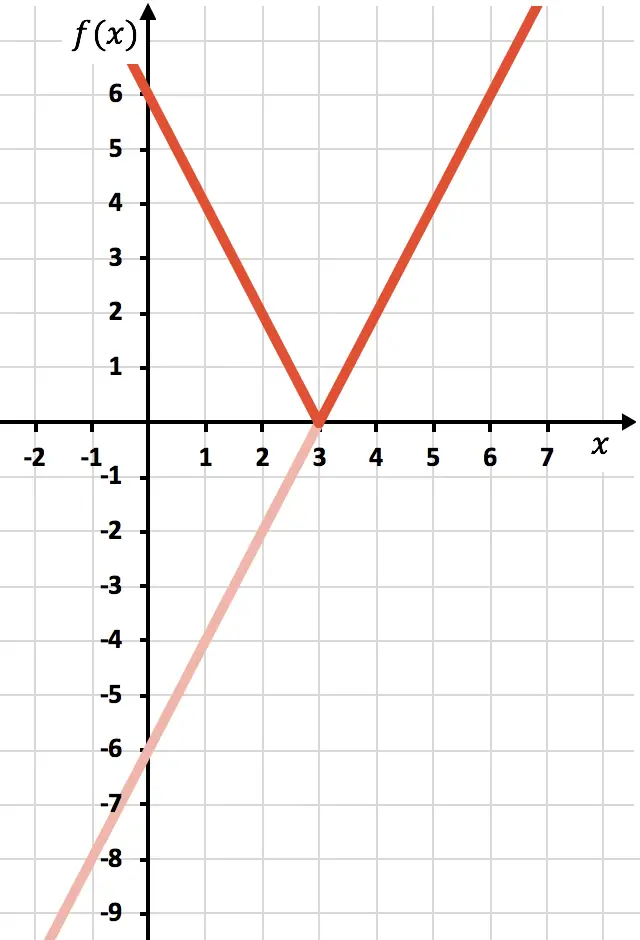
最后我们消除位于 X 轴下方的函数迹:

这样,我们就已经用绝对值来表示函数了。正如您所看到的,唯一改变的是我们必须反转位于 OX 轴下方的函数部分。因此,任何具有绝对值的函数的图形将始终位于正半Y轴一侧。
另一方面,回顾一下概念,从图中我们可以推断出前面的绝对值函数的域完全由实数组成。另一方面,所述具有绝对值的函数的范围或范围仅由正数和零组成。
解决了绝对值函数的练习
练习1
将以下具有绝对值的函数表示为分段函数:
![]()
首先,我们要看看函数什么时候为负数。为此,我们将绝对值设置为零并求解方程:
![]()
![]()
我们表示在线路上找到的值:
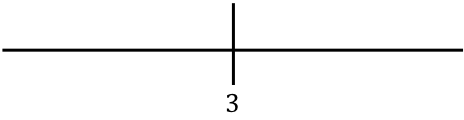
现在我们评估函数每个区间中的一个点(不带绝对值),以找出该函数在线的每个部分中实际具有的符号:
![]()
例如,我们取任何小于 3 的点
![]()
![]()
![]()
积极的
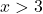 例如,我们取任何大于 3 的点
例如,我们取任何大于 3 的点
![]()
![]()
![]()
消极的
没有绝对值的函数在 x>3 区间内将为负值。因此,我们必须通过改变该区间内的符号来用破折号来表达该函数:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] -(-x+3) & \text{si} & x\ge 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-f7cfaaff9890b356f1db6805ed94dbb8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] x-3 & \text{si} & x\ge 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d249715b500ad03c44ab6ab5838e32e8_l3.png)
练习2
求以下具有绝对值的函数的分段表达式:
![]()
我们需要做的第一件事是确定函数何时为负值。为此,我们需要将绝对值参数设置为零并求解方程:
![]()
![]()
![]()
![]()
![]()
现在我们表示右侧获得的函数的根:
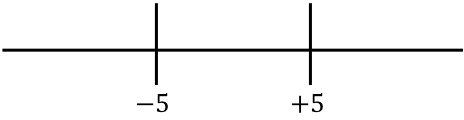
我们看看哪个符号在直线的每个区间内具有不带绝对值的函数:
![]()
例如,我们取任何小于-5的点
![]()
![]()
![]()
![]()
积极的
![]()
例如,我们取 -5 和 +5 之间的任意点
![]()
![]()
![]()
![]()
消极的
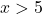 例如,我们取任何大于 5 的点
例如,我们取任何大于 5 的点
![]()
![]()
![]()
![]()
积极的

因此,没有绝对值的函数只会在区间 -5<x<5 内为负值。因此,我们需要通过仅改变该区间的符号来分段表达该函数:
![\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -(3x^2-75) & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”408″ style=”vertical-align: 0px;”></p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e0fad2e3a9e1a6d1edcde507e60230b_l3.png)
![\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -3x^2+75 & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”394″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-5f9638fe87ad09d7dbcdb8e30a16688f_l3.png)