共面线

在此页面上，您将了解两条线共面时的含义。您还可以看到两条线何时共面，此外，您还可以找到共面线的示例和已解决的练习。

什么是两条共面线？

在解析几何中，共面线的定义如下：

当两条直线在同一平面内时，它们共面。因此，共面线只能是割线、平行线或重合线。

此外，两条共面线足以完全定义一个平面。虽然显然一个平面可以有两条以上的共面线，但实际上每个平面都包含无限多条线。

另一方面，如果两条线不共面，则意味着它们相交。

共面线的示例

为了让您更好地理解共面线的概念，下面是一个包含三条线的示例：

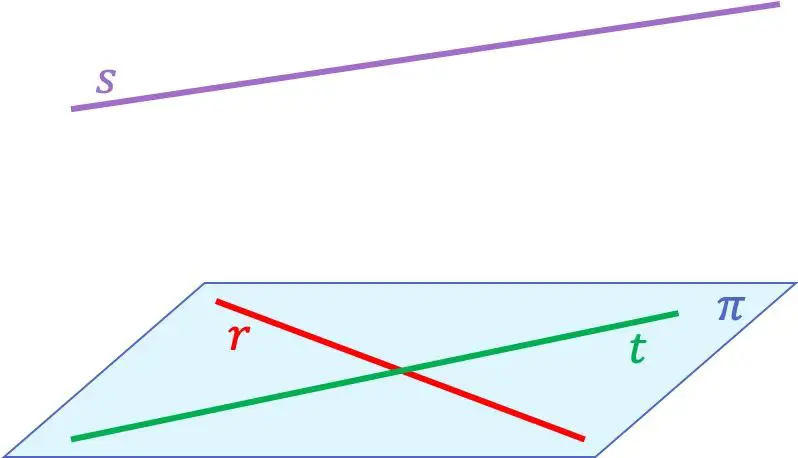
在这种情况下，行

和

它们是共面的，因为它们属于同一平面。相反，直线

与其他两条线不共面，因为它与其他两条线相交

和

如何知道两条线是否共面？

正如我们在上面对共面线的解释中看到的，这些线只能是割线、平行线或重合线。换句话说，两条交叉线永远不会共面。

因此，要知道两条直线是否共面，必须确定它们之间的相对位置，如果它们是两条相交、平行或重合的直线，则说明它们是共面的。

因此，要检查两条线的共面性，首先必须知道如何计算两条线在空间中的相对位置。如果您仍然不熟悉这个概念，最好先查看链接，您可以在其中找到完整的解释以及示例、练习和已解决的问题。

解决了共面线的练习

例如，我们将解决共面线上的典型练习：

• 判断下列两条直线是否共面：

我们必须做的第一件事是找到两条线之间的相对位置，为此，我们必须使用相同类型的方程来表达两条线。然后我们将穿过直线

从一般（或隐式）方程到参数方程：

所以每条线的方向向量为：

两条线的方向矢量的坐标成比例，因此只能是重合线或平行线。因此，在这种特殊情况下，不需要计算精确的相对位置，因为平行线和重合线是共面线。所以这两条线是共面的。