什么是向量（数学）？ -Mathority

在此页面上，您将找到有关向量的所有内容：它们是什么、它们的特征、它们如何计算、如何对向量进行运算、存在的不同类型……

什么是向量？

向量的数学定义如下：

在数学中，向量是从一个点（称为原点）到另一点（称为终点）的有向线段。

例如，在下图中，您可以看到向量

$\vv{AB}$

它以 A 点为原点，以 B 点为终点。

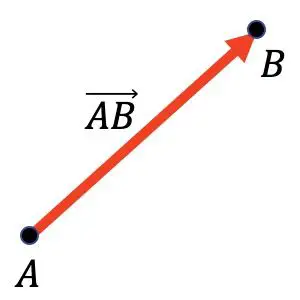
矢量主要用于数学（特别是几何学）和物理学中，以图形方式表示矢量力。

向量的特征

了解了向量的数学含义后，现在让我们看看它们的属性是什么。

每个向量具有以下几何特征：

方向：矢量的方向是包含该矢量的线或与其平行的任何线的方向。换句话说，向量的方向就是它所在的线。
方向：向量的方向是该向量的方向，由其箭头指示。
模（或幅度）：向量的模是其长度，对应于向量的数值。因此，向量均值越大，代表的向量量就越大。
应用点：矢量的应用点是该矢量的原点。

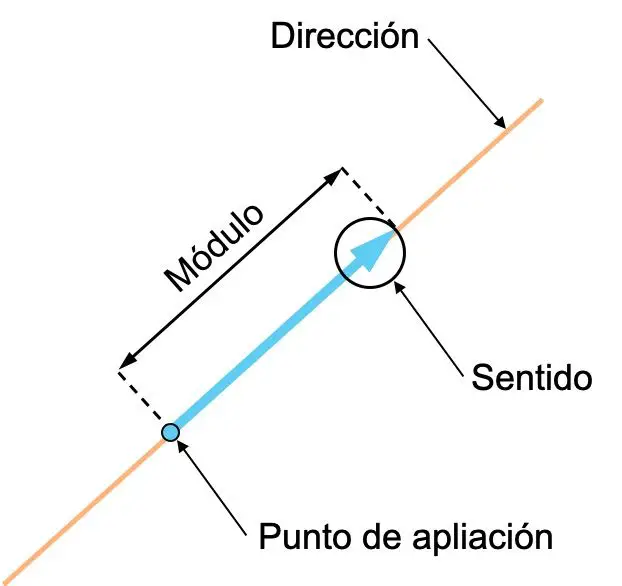
方向和向量方向的概念经常令人困惑，因此区分它们之间的差异很重要。看下面的例子，有两个向量，它们的方向相同，但含义不同：

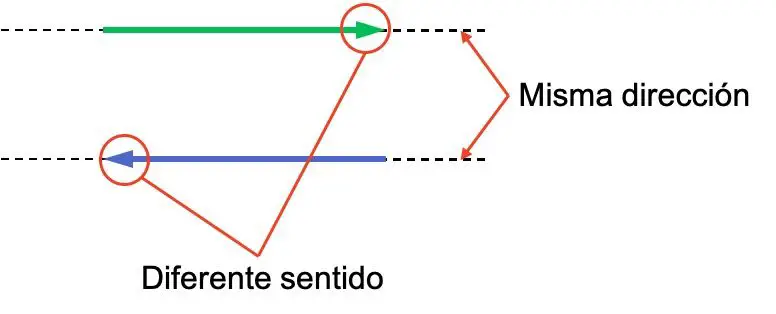
这两个向量具有相同的方向，因为它们是平行的。相反，他们的方向是相反的，因为他们面向后。

向量的组成部分

我们刚刚看到向量用箭头图形表示，但向量也可以用向量的分量（或坐标）数字表示。

例如，如果我们在图中表示以下向量：

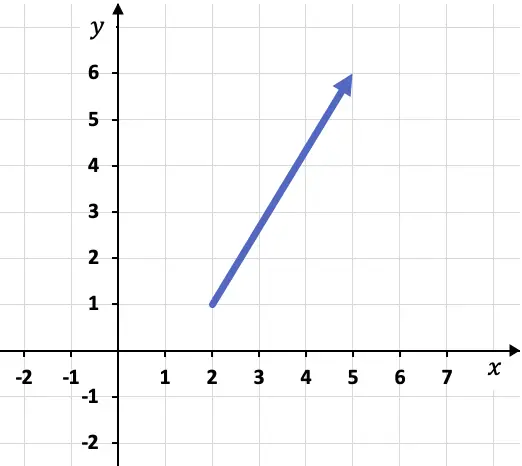
要计算向量的分量，我们必须首先确定其原点和终点的坐标，即向量的起点和终点。在这种情况下，向量的原点和终点是：

向量原点：A(2,1)

矢量终点：B(5,6)

因此，要找到向量的坐标或分量，只需减去终点减去原点即可：

$\begin{aligned} \vv{AB} & = B- A \\[2ex] & = (5,6)- (2,1) \\[2ex] &= (5-2 \ , \ 6-1) \\[2ex] &= (3,5) \end{aligned}$

因此图中表示的向量的分量为：

$\vv{\bm{AB}}\bm{=(3,5)}$

向量运算

添加向量

要对两个向量进行数值加法，必须将它们各自的分量相加。或者换句话说，两个向量的X坐标相加并且与Y坐标相同。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} + \vv{\text{v}} = (\text{u}_x + \text{v}_x \ , \ \text{u}_y + \text{v}_y) \end{array} \end{empheq}$

所以你可以看到这是如何完成的，我们将添加以下两个向量：

$\vv{\text{u}} = (2,3) \qquad \vv{\text{v}}=(4, -1)$

$\begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(2,3) +(4,-1) \\[2ex] & = (2+4,3+(-1)) \\[2ex] & = \bm{(6,2)} \end{aligned}$

两个向量也可以从它们的图形表示中相加。为此，通常使用平行四边形规则或定律，但方法有很多。您可以在此处查看有关如何以图形方式添加两个向量的示例和已解决的练习。

矢量减法

要以解析方式减去两个向量，必须减去它们各自的分量。即两个向量的X坐标相减，与Y坐标相同。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} - \vv{\text{v}} = (\text{u}_x - \text{v}_x \ , \ \text{u}_y - \text{v}_y) \end{array} \end{empheq}$

例如，我们将减去以下两个向量：

$\vv{\text{u}} = (3,1) \qquad \vv{\text{v}}=(2, -4)$

$\begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(3,1) -(2,-4) \\[2ex] & = (3-2,1-(-4)) \\[2ex]& = (3-2,1+4) \\[2ex] & = \bm{(1,5)} \end{aligned}$

与加法一样，您也可以使用 2 个向量的表示形式来减去它们。为此，通常使用三角法则或定律，但有几种方法。您可以通过示例以及有关如何以图形方式减去两个向量的已解决练习来查看它们。

向量的模

正如我们在本页开头所看到的，向量的大小对应于该向量的长度。那么，向量的长度（或大小）可以根据其分量来确定。

考虑任意向量：

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

要找到平面中向量的大小，我们必须应用以下公式：

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2} \end{empheq}$

例如，我们将使用以下公式计算以下向量的大小：

$\vv{\text{u}} = (3,-4)$

$\lvert \vv{\text{u}} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{9+16}=\sqrt{25} = \bm{5}$

虽然看起来很简单，但确定矢量的大小可能很复杂。如果您想查看更多示例并通过向量模块的已解决练习进行练习，我们建议您访问此链接页面。

向量乘以标量

要以数值方式计算向量与数字（或标量）的乘积，向量的每个分量都必须乘以该数字。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}\vv{\text{u}} = (\text{u}_x,\text{u}_y)\\[4ex]k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y) \end{array} \end{empheq}$

在下面的通用示例中，您可以看到如何保持向量的方向，而不管标量的符号如何。另一方面，向量的方向取决于它相乘的数字的符号。

下面您可以看到如何求向量和数字的乘积的数值示例：

$\vv{\text{u}} =(3,-2)$

$4\cdot \vv{\text{u}} =(4 \cdot 3 \ , \ 4 \cdot (-2)) = \bm{(12,-8)}$

标量积

在解析几何中，点积是一种向量运算，它将两个向量相乘并将它们转换为实数。

因此，两个向量的点积公式如下：

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \cdot \vv{\text{v}} = \text{u}_x\cdot \text{v}_x + \text{u}_y\cdot \text{v}_y \end{empheq}$

下面是计算两个向量之间的点积结果的示例：

$\vv{\text{u}} = (4,2) \qquad \vv{\text{v}} = (-1,3)$

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(4,2)\cdot (-1,3) \\[1.5ex]&=4\cdot (-1) + 2 \cdot 3 \\[1.5ex] & = -4+6 \\[1.5ex] & =\bm{10} \end{aligned}$

在此链接中，您可以看到点积的更多示例。此外，您还会找到另一种求两个向量之间点积的方法，这种类型的运算的性质用向量和练习逐步解决。

矢量积

虽然它们的名称非常相似，但点积和叉积却完全不同。

叉积，也称为叉积，是空间中（R3中）两个向量之间的运算，即它们是三坐标向量。

因此，如果我们有任意两个三维向量：

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

两个向量的叉积等于以下 3×3 行列式的结果：

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix} \end{empheq}$

其中向量

$\vv{i}, \vv{j},\vv{k}$

分别是X、Y、Z轴方向的单位向量。

此外，所得向量的方向垂直于两个相乘向量。

正如您所猜测的，解决此类运算比以前的运算更困难，因此，我们有一整页详细说明如何计算两个向量之间的叉积。因此，如果您有兴趣，我们建议您访问并练习已求解的向量积练习。

混合产品

三个向量的混合积，也称为三重点积，是三个向量之间的连续乘法，涉及两种不同类型的运算：点积和向量积。因此，两个向量运算的组合给出一个标量（实数）。

具体地，混合乘积包括计算两个向量的向量乘积，并且随后将所获得的结果与第三向量相乘。看一下公式：

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.3pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}}) \end{empheq}$

与向量积一样，求解向量之间的混合积并不容易。因此，我们建议您看一下三个向量的混合乘积的解释，您将在其中找到示例、已解决的练习以及该向量运算的几何意义。

向量类型

向量有许多不同类型，但需要了解的最重要的定义是：

单位向量：模等于1的向量。
固定向量：当向量的原点应用于固定点时，向量是固定的。
自由向量：当向量的作用点未定义但为自由点时，向量是自由的。
共线向量：如果两个或多个向量共享相同的作用线（向量所在的线），则它们是共线的。
等价向量：如果两个向量具有相同的大小、相同的意义和相同的方向，则它们是等价的（尽管它们可以有不同的应用点）。
链接向量：链接向量是也作用于同一直线的等花粉向量。
相反向量：如果两个向量具有相同的大小和相同的方向但方向不同，则它们相反。
位置向量：位置向量是以点(0,0)（坐标原点）为原点的向量。
竞争向量：两个或多个向量的作用线经过同一点（即相交）时，它们是并发的。
平行向量：两个或多个向量如果具有相同的方向，则无论其方向如何，它们都是平行的。
垂直向量：当两个向量的方向形成 90° 角时，它们是垂直（或正交）的。
正交向量：如果两个或多个向量彼此垂直，并且它们是幺正的（它们的大小等于 1），则它们是正交向量。
共面向量：两个或多个向量包含在同一平面中时是共面的。

两个向量之间的角度

要找到两个给定向量之间的角度，我们必须应用以下公式：

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

金子

$\lvert \vv{\text{u}} \rvert$

和

$\lvert \vv{\text{v}} \rvert$

是向量的模

$\vv{\text{u}}$

和

$\vv{\text{v}}$

分别。