在此页面上,您将找到牛顿二项式(或二项式定理)及其公式的解释。您还可以看到如何使用塔塔利亚(或帕斯卡)三角形来简化这一过程。此外,您还将找到牛顿二项式及其所有属性的分步解答练习。最后,我们将解释这个非常特殊的定理起源背后的好奇心。
什么是牛顿二项式?
在数学中,牛顿二项式,也称为二项式定理,是一个可以让您轻松计算二项式幂的公式。换句话说,牛顿二项式由一个可以求解(a+b) 形式的代数表达式的公式组成。
显然,这个定理是以物理学家、数学家和哲学家艾萨克·牛顿爵士的名字命名的。然而,在这方面存在一些争议,因为在中东文本中已经发现了该定理的使用。下面我们就深入探讨一下这个数学公式的由来。
牛顿二项式公式
正如我们在牛顿二项式的定义中看到的,该定理用于求解二项式的幂。但是……牛顿二项式是如何应用的?或者,换句话说,牛顿二项式公式是什么?
牛顿二项式的数学公式如下:
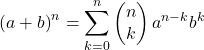
或同等学历:
![]()
该公式对于理解牛顿二项式的概念来说有点复杂,因此我们在下面列出了最低次二项式的幂,以便您更好地理解它:

正如您所看到的,展开二项式 时,第一项 (a) 的指数减少,而第二项 (b) 的指数增加,就像组合数的较低元素增加一样。
因此,要使用二项式定理,您需要知道如何求解组合数,即类型的代数表达式
![]()
。因此,在我们查看如何计算牛顿二项式的示例之前,让我们简要回顾一下组合数。
组合数
要确定组合数(或二项式系数),您必须应用以下公式:
![]()
金子
![]()
和
![]()
这些是阶乘数。我们还请记住,阶乘数是通过将所有 1 的正整数乘以所述数来计算的:
![]()
作为示例,我们将找到一个组合数,以便您了解它是如何完成的:
![]()
组合数也可以通过计算器用 键确定
![]()
牛顿二项式示例
现在我们知道什么是二项式定理,让我们看看如何使用两个数值示例来应用牛顿二项式公式。
实施例1
- 应用牛顿二项式计算以下二项式的幂:
![]()
显然,由于这个二项式是平方的,所以也可以用显着恒等式的公式来求解( 如何求解显着恒等式),但我们将以二项式定理为例进行计算。
首先,我们必须应用牛顿二项式公式:
![]()
在这种情况下 n=2,因此:
![]()
仔细看,一开始我们将第一项 (x) 提高到可能的最大值,在本例中为 2。另一方面,我们将第二项 (3) 提高到可能的最小值,它始终为 0。但是当我们向右移动时,我们需要将第一项提高到比以前更低的数字,将第二项提高到比以前更高的数字。
现在我们来计算组合数:
![]()
我们求解权力:
![]()
最后,我们计算乘法:
![]()
实施例2
现在我们要解决一个稍微困难一点的问题。
- 应用牛顿二项式公式求以下二项式的幂:
![]()
二项式定理的公式为:
![]()
在这种情况下,n=3,因此:
![]()
我们计算组合数:
![]()
现在我们解决权力问题,为此,记住以下两个属性很重要:
• 当单项式升为指数时,系数和变量升为相同的指数 →
![]()
• 任何项变为 0 都会得到 1 →
![]()
因此,我们通过这两个属性找到权力:
![]()
![]()
最后,我们将这些项相乘:
![]()
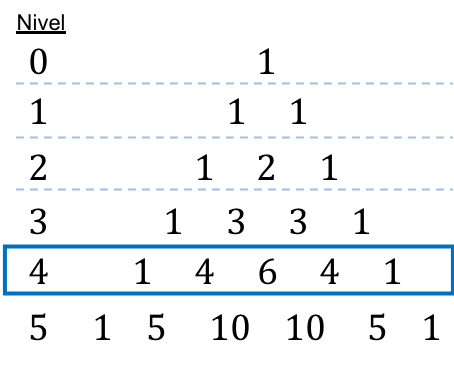
牛顿二项式和塔塔利亚(或帕斯卡)三角形
正如您在上面的示例中看到的,计算组合数有点乏味。这就是为什么我们要教你一个技巧,这样你就不必解组合数,因为你可以使用塔塔利亚三角形(也称为帕斯卡三角形)直接找出它们的价值。
如果您不知道它是什么,塔塔利亚三角形,也称为帕斯卡三角形,是排列成三角形的数字的数学表示。
要构建塔塔利亚或帕斯卡三角形,我们必须从三角形的顶点开始,该顶点始终为 1,然后确定下面的线的数量。以下各行中的每个数字都等于紧邻其上方的两个数字之和,但行尾始终为 1 除外。
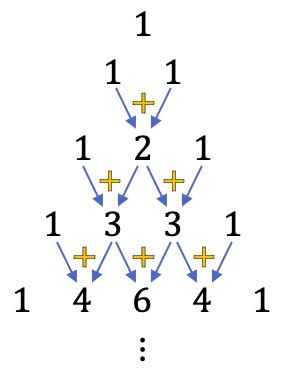
那么,塔塔利亚三角形中的每一个数字都对应着一个组合数的结果,看下图:
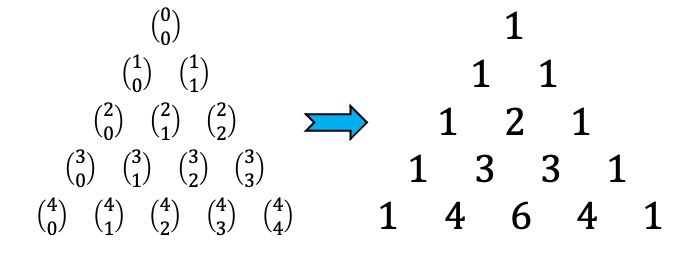
例如,二项式系数
![]()
等于3,因为在塔尔塔利亚三角形中,它的位置有一个3。
因此,我们可以使用塔塔利亚(或帕斯卡)三角形更快地求解牛顿二项式,因为它使我们无需计算组合数。
例如,如果我们想要对二项式进行以下增强:
![]()
通过应用牛顿二项式法则,我们得到以下代数表达式:
![]()
那么,我们不用一一计算组合数,而是简单地将每个组合数替换为塔塔利亚三角形对应的系数。在这种情况下,二项式被提升到第三层,因此它对应于三角形的第三层:
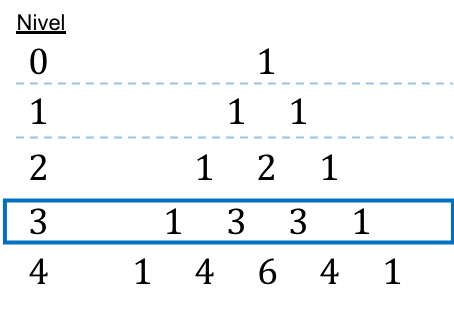
![]()
现在我们要做的就是完成剩下的操作:
![]()
![]()
正如您所看到的,塔塔利亚(或帕斯卡)三角形用于以更简单、更快的方式计算牛顿二项式,正如我们所展示的。这就是我们建议使用它的原因。
总结到目前为止我们所看到的一切,我们给您留下一张图像,显示牛顿二项式与塔塔利亚(或帕斯卡)三角形的数字的表达式是什么样的:

负牛顿二项式:减法幂
到目前为止,我们解决的所有牛顿二项式的例子都是加法。另一方面,当二项式的两项中的一项具有负号时,过程保持相似,但略有变化。
当二项式的一项为负时,也就是说它是 (ab) n类型的减法,牛顿二项式的展开式的符号必须以 + – + – + – + – … 的形式交替。
下面我们用二项式定理和已经存在的塔尔塔利亚三角形的系数导出了前5次负二项式的幂,这样您就可以直接找到您需要的二项式表达式:

牛顿二项式的性质
牛顿二项式表达式具有以下特点:
- 分解牛顿二项式总是会得到比二项式次数多的一项。或者换句话说,对于这对
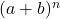
他们受到影响
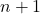
条款。
- 元素的力量

从…开始
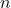
并且在最后一个季度下降至 0。
- 元素的力量
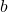
它们朝另一个方向发展:它们从 0 开始并增加,直到达到
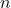
在最后一个学期。
- 对于牛顿二项式的每个元素,指数之和

和
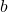
等于
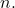
- 牛顿二项式表达式第一项的系数始终为 1(正),第二个系数相当于二项式的指数(正或负)。
计算牛顿二项式的第 k 项
虽然这很不寻常,但我们有时会遇到这样的问题:我们不进行牛顿二项式展开式,而是要求确定牛顿二项式的第 k 项,即占据位置 k 的项。
因此,要计算牛顿二项式中占据位置 k 的项,我们必须使用一个公式,该公式取决于二项式是加法还是减法:
- 如果牛顿二项式为正,则第 k 项的值通过以下公式计算:
![]()
- 如果牛顿二项式为负,则第 k 项的值由以下公式确定:
![]()
例如,我们将找到以下 5 次二项式的第四项:
![]()
由于它是由和组成的二项式,因此我们应用第一个公式:
![]()
我们将公式中的变量替换为其对应的值:
![]()
我们进行以下操作:
![]()
![]()
![]()
这样我们就计算出了牛顿二项式展开式的第四项,而无需计算所有其他项。
解决了牛顿二项式的练习
现在我们已经解释了什么是二项式定理,我们为您提供了几个有关牛顿二项式定理的已解决的分步练习,以便您进行练习。另请记住,您可以在评论中向我们留下任何问题或建议。
练习1
使用二项式定理展开以下二项式幂:
![]()
我们首先使用牛顿二项式公式:
![]()
由于二项式是 3 次方,所以我们看塔塔利亚三角形的第三层,直接求组合数:

![]()
我们行使以下权力:
![]()
最后我们乘以:
![]()
![]()
练习2
用牛顿二项式公式计算以下幂:
![]()
首先,我们应用牛顿二项式公式:
![]()
由于二项式是三次方,我们看帕斯卡三角形的第三层就可以直接知道组合数的值:

![]()
我们计算单项式的幂:
![]()
最后,我们进行乘法:
![]()
![]()
练习3
使用牛顿二项式公式展开以下多项式:
![]()
首先,我们使用牛顿二项式公式。但由于括号内有减法,因此我们必须交换每一项系数的符号:
![]()
由于二项式是三次方,所以我们看塔塔利亚三角形的第三层来直接计算组合数:

![]()
我们行使以下权力:
![]()
我们解决乘法:
![]()
![]()
练习4
使用以下公式求以下牛顿二项式的展开表达式:
![]()
我们必须应用牛顿二项式的一般公式,但由于在这种情况下我们在括号中进行减法,所以我们必须交替每一项的符号:
![Rendered by QuickLaTeX.com \begin{aligned}(4x-3y)^4 = & \begin{pmatrix} 4 \\ 0 \end{pmatrix} (4x)^4 \cdot (3y)^0-\begin{pmatrix} 4 \\ 1 \end{pmatrix} (4x)^3 \cdot (3y)^1+\begin{pmatrix} 4 \\ 2 \end{pmatrix} \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - \begin{pmatrix} 4 \\ 3 \end{pmatrix}(4x)^1 \cdot (3y)^3+\begin{pmatrix} 4 \\ 4 \end{pmatrix} (4x)^0 \cdot (3y)^4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7a8620bd23846e1f98f7646cbd51dbc5_l3.png)
由于二项式被提升到第四级,我们查看塔塔利亚三角形的第 4 级来直接找到组合数:
![Rendered by QuickLaTeX.com \begin{aligned}(4x-3y)^4= & \ 1\cdot (4x)^4 \cdot (3y)^0-4\cdot (4x)^3 \cdot (3y)^1+6 \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - 4 \cdot (4x)^1 \cdot (3y)^3+1 \cdot (4x)^0 \cdot (3y)^4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-128e8baa45ddd7d74703c9dfd4a19b06_l3.png)
我们实现了所有的权力:
![]()
最后,我们解决乘法:
![]()
![]()
练习5
确定以下二项式表达式展开式中的第七项:
![]()
由于它是负二项式,因此我们必须使用以下公式:
![]()
我们想要确定第7项,并且二项式的10次方,因此将这些值代入公式就变成:
![]()
因此,了解该术语就足以进行操作:
![Rendered by QuickLaTeX.com \begin{aligned} T_7 & = (-1)^{6} \begin{pmatrix} 10 \\ 6 \end{pmatrix} (2x)^{4} \cdot (5y)^{6} \\[2ex] & = 1 \cdot 210\cdot 16x^4 \cdot 15625y^6 \\[2ex] & = \bm{52500000x^4y^6} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ded0622cbba2bff0563c2f9982c05142_l3.png)
牛顿二项式的历史
尽管二项式定理的起源归因于英国著名科学家艾萨克·牛顿(Isaac Newton,1642-1727),但实际上该定理的第一个表述是由波斯工程师 Al-Kariji 在 1000 年左右首次发现的,甚至还发现: 13世纪,中国数学家杨辉和朱士杰已经知道小次数的二项式展开式。
后来,在 17 世纪,牛顿在前任数学家奠定的基础上扩展了二项式定理。利用数学家约翰·沃尔斯的插值和外推方法以及广义指数的概念,他能够将多项式表达式转换为无穷级数。
1665年左右,牛顿成功证明了二项式定理的指数n也可以是有理指数,也就是说,如果指数是分数,也可以求解二项式的幂。另一方面,在负指数的情况下也得到了证明。而且,令人惊讶的是,他发现这两个表达式的发展是项的无穷级数。
正是有了这个发现,牛顿开始质疑无限级数和有限多项式表达式之间的关系,并推断出无限级数可以像有限多项式表达式一样进行数学运算。尽管牛顿从未发表过该定理,但约翰·沃尔斯最终于 1685 年发表了这一发现,并将这一发现归功于牛顿。