二次方程或二次方程是 2 次方程,其中一项的最大指数等于 2。这意味着该方程最多可以有两个不同的解,尽管它也可能有唯一解或一个都没有。
要计算二次方程的解或根,我们可以遵循两种不同的过程:通过二次公式或通过因式分解表达式。在本文中,我们将讨论这两种方法并为您提供一些实际练习。尽管在之前我们将澄清一些概念,以便很好地理解整个解释,并且您可以从阅读中获得最大收益。
二次方程的类型
二次方程之间的主要分类是基于表达式本身的结构。因此,这些表达式的标准或通常结构如下: ax² + bx + c 。这种常见形式相当于一个完整的方程,但是当存在空项或空项时,结构可能会发生变化,这就是不完整方程出现的地方。接下来,我们将更详细地解释所有类型的特征。
完全二次方程
正如我们已经说过的,我们有完整的二次方程,它们的所有系数 a、b 和 c 均非零。因此,该表达式严格遵循结构 ax² + bx + c,因为它具有所有项:二次项、线性项和独立项。这种类型的示例如下:x² + 2x + 1 = 0。
不完全二次方程
对于不完备方程,我们可以根据哪个系数为零来区分。请记住,如果这个解释不能解决您的疑问,下面是一张图片,您可以在其中找到逐步解释的所有案例。
- 不完全方程 (b = 0):在第一种情况下,我们找到一个遵循以下结构的表达式:ax² + c = 0。由此,我们得到两个结果:分数 c/a 的根的负数和正数。
- 不完全方程 (c = 0):当我们具有 ax² + bx = 0 的形式时,我们必须对方程进行因式分解以获得表达式 x (ax + b) = 0。因此,我们将有两个解:x = 0 和 x = – b/a。
- 不完全方程 (b = c = 0):在这种情况下,我们有一个方程 ax² = 0,并且只有一个可能的解,即 x = 0。
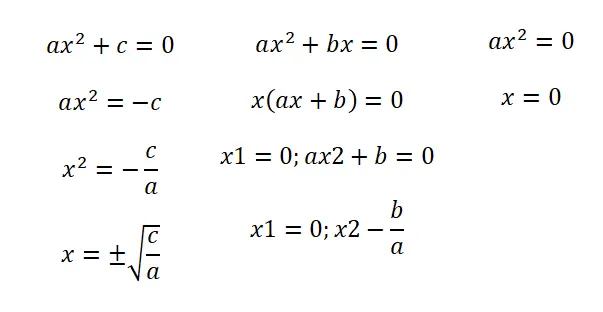
值得一提的是,我们教给您的程序可以让您在求解不完整方程时速度更快。但是,在所有情况下,您都可以使用我们下面将教您的二次公式,您只需在不存在的系数中写入零即可。
二次方程的公式
为了求解二次方程(ax² + bx + c = 0),我们需要应用一般公式或二次公式,然后我们需要代入数学表达式中每个字母对应的数值。
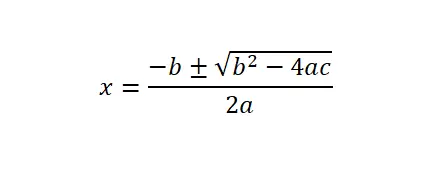
另外,需要解释的是,判别式 (Δ)是表达式 b² – 4ac,它位于平方根下方。从这个数学概念我们可以知道这个二次方程有多少个解。基本上,有三种选择:判别式为负(没有实数解),判别式为零(只有一个解),或者判别式为正(有两个解)。
求解完全二次方程的示例
尝试求解以下二次方程: 2x²+4x-6=0并用下面的结果检查您的结果。我们建议您遵循以下过程:分析方程的类型(识别零项),计算判别式以了解现有解的数量,最后用公式求解建议的方程。
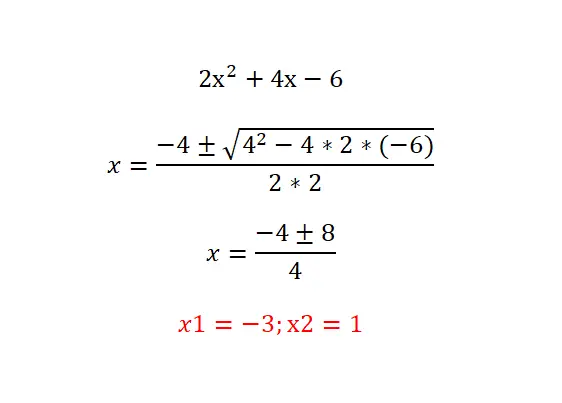
阶乘二次方程
求解二次方程的第二种方法是因式分解。因此,要因式分解多项式(在我们的例子中是二次多项式),我们可以使用不同的方法。尽管一般来说,当涉及到这种类型的方程时,它们通常可以通过通用项进行因式分解。如果没有,您可以尝试应用Notable Identities ,但通常在这些情况下您不需要知道任何其他方法。
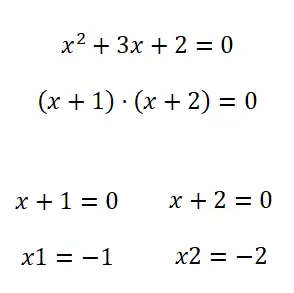
二次方程练习及解
下面您将找到一系列关于完全和不完全二次方程的练习。通过这种方式,您将回顾本文中解释的所有理论,并且会更清楚如何在练习中应用它。我们建议您尝试自己解决它们,并且仅在完成它们或遇到困难时才查看解决方案。也就是说,你现在就可以开始解决练习了。
练习1
求解以下二次方程:
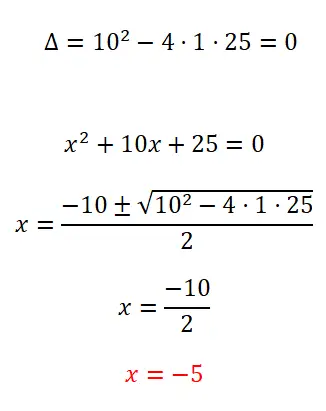
- 我们首先计算判别式,以了解可能的解决方案的数量。
- 由于这是一个完整的二次方程,我们应用二次公式并求解计算。
- 我们得到未知 x 的值。
练习2
求解以下二次方程:
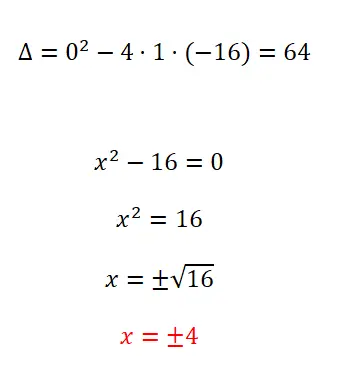
- 我们首先计算判别式。
- 由于我们有一个不完全二次方程,其中 b = 0,因此我们应用此类方程的标准。
- 我们解算得到结果,不能忘记±号。
练习3
求解以下无序二次方程:
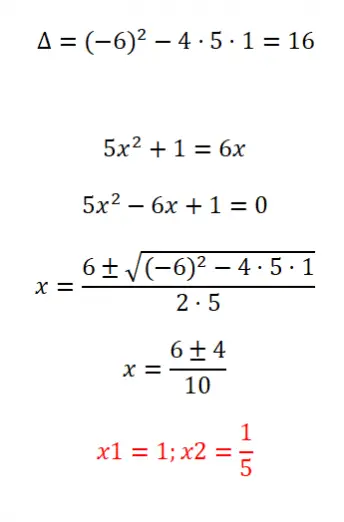
- 我们首先计算方程的判别式。
- 在应用该公式之前,我们需要根据结构 ax² + bx + c = 0 对方程进行排序。
- 然后我们应用一般公式。
- 最后我们得到结果。
练习4
通过因式分解求解以下二次方程:
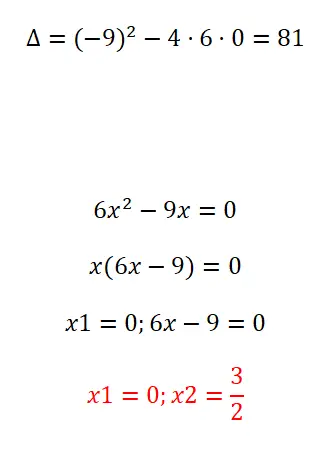
- 我们首先计算判别式。
- 接下来,我们提取 x 的公因数。
- 所以第一个解是 x = 0。
- 第二个是 x = 3/2。
练习5
求解如下所示的完整二次方程:
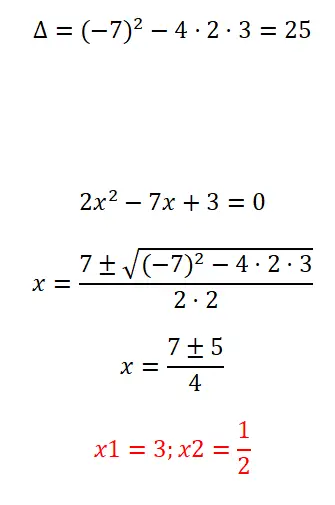
- 与往常一样,我们计算判别式以找出所讨论的方程有多少个解。
- 接下来,我们应用二次公式,因为它是一个完整的方程。
- 最后,我们表达方程的结果。
练习6
用我们提供的分数求解二次方程:
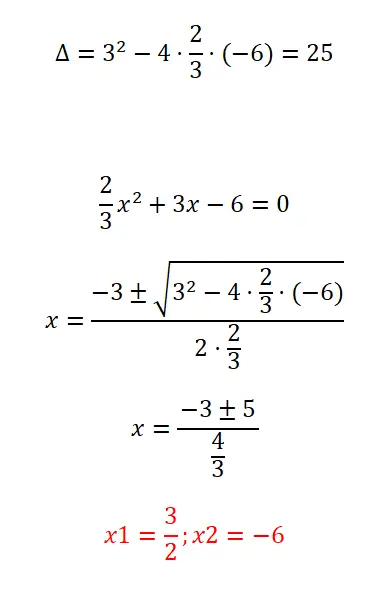
- 我们首先计算表达式的判别式。
- 接下来,我们应用二次公式,考虑到系数“a”是由分数组成的。
- 我们解决计算。
- 我们已经有了方程的两个根。
练习7
求解以下二次方程:
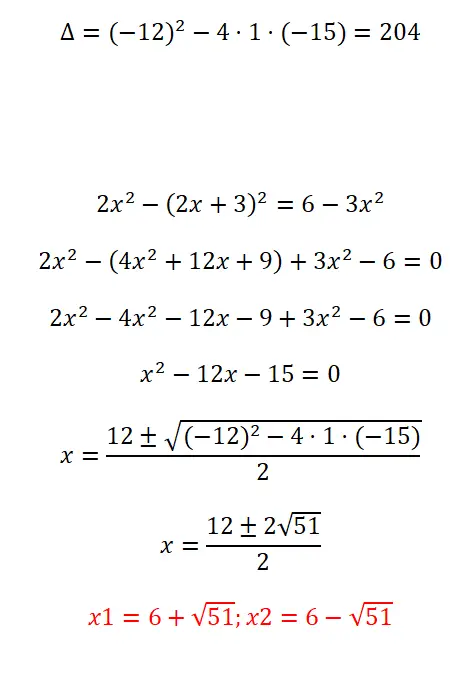
- 我们首先计算判别式。
- 在应用公式之前,我们需要简化表达式并给出 ax² + b + c = 0 的形式。
- 我们代入公式中的所有系数并求解计算。
- 最后我们得到结果。
练习8
求解以下二次方程的证明:
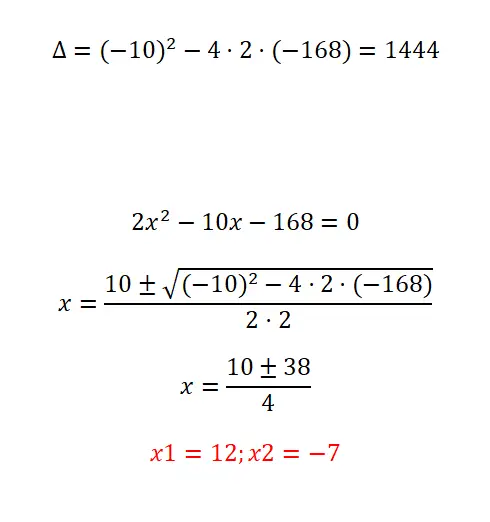
- 我们首先计算判别式。
- 正如您所看到的,这是一个简单的二次方程,尽管它具有相当大的系数。因此,我们在应用公式的时候需要小心操作。
- 最终我们得到了两种可能的解决方案。